Op-amp Subtractor or Difference Amplifier

Subtractor or Difference Amplifier

Similar to the summer circuit, the subtraction of two input voltages is possible with the help of op-amp circuit, called subtractor or difference amplifier circuit.

The circuit diagram is shown in the Fig. 2.28.1.

To find the relation between the inputs and output let us use Superposition principle.

Let V_ol be the output, with input V₁ acting, assuming V₂ to be zero.

And V_o2 be the output, with input V₂ acting, assuming V₁ to be zero.

Case 1 : With V₂ zero, the circuit acts as an inverting amplifier. Hence we can write, Vol = - (R_f / R₁) V₁ ... (2.28.1)

Case 2 :

While with V₁ as zero, the circuit reduces to as shown in the Fig. 2.28.2.

Let potential of node B is V_B.

The potential of node A is same as B i.e. V_A = V_B.

Applying voltage divider rule to the input V₂ loop

Equating the equations (2.28.3) and (2.28.4)

Substituting V_B from equation (2.28.2) in equation (2.28.5) we get

Hence using Superposition principle,

Now if the resistances are selected as R₁ = R₂,

Key Point Thus the output voltage is proportional to the difference between the two input voltages. Thus it acts as a subtractor or difference amplifier.

If R₁ = R₂ = R_f is selected,

V_o = V₂ – V₁

But by selecting proper values of R₁ , R₂ and R_f, we can have the subtraction of two inputs with appropriate strengths like

V_o = aV₂ -b V₁ 

Thus using adders and subtractors, various mathematical equations like

V_o = (aV₁ + bV₂) - (cV₃ + dV₄) can be solved. In such equation, two adder circuits are used and the outputs of these circuits are used as input to a subtractor to obtain the required equation.

Example 2.28.1 Design an op-amp circuit to give an output voltage V_o = 4V₁ -3V₂ + 5V₃ -V₄. Where V₁, V₂, V₃ and V₄ are inputs.

Solution : The positive and negative terms can be added seperately using two adders and then subtractor can be used.

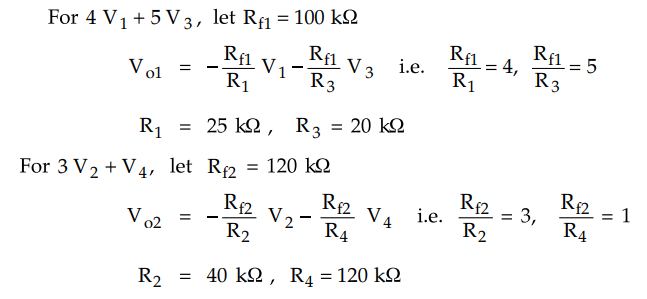
Use the subtractor with all the resistances of same value of R = 100 kΩ.

Output of the subtractor is V_o = V_o2 - V_o1

V_o = - 3V₂ -V₄ - (- 4V₁ - 5V₃)= 4V₁ - 3V₂ + 5V₃ - V₄

The designed circuit is shown in the Fig. 2.28.3

Example 2.28.2 Find V₀ for the given circuit.

Dec.-08, May-16, Marks 8

Solution : Use superposition principle.

Case 1 : Assume V₁ and V₂ acting and V₃ and V₄ = 0V

The circuit works as inverting summer circuit, as shown in the Fig. 2.28.4 (a).

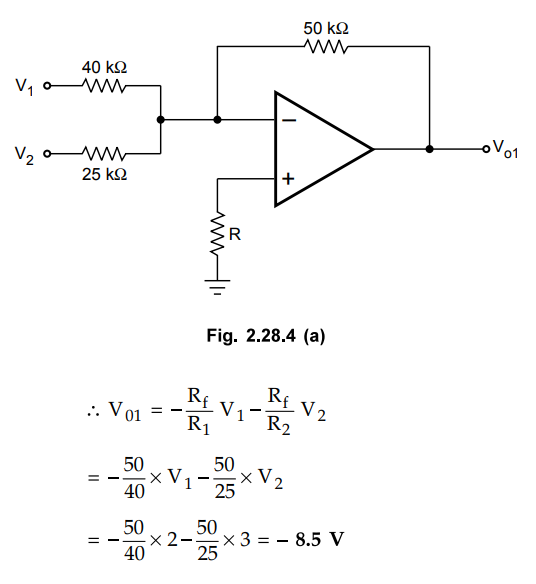
Case 2 : Assume V₃ acting and V₁ = V₂ = V₄ = 0

The circuit is as shown in the Fig. 2.28.4 (b). It acts as a noninverting amplifier.

Case 3 : Assume V₄ acting and V₁ = V₂ = V₃ = 0

The circuit is as shown in the Fig. 2.28.4 (c).

Example 2.28.3 Design an adder-subtractor circuit for V_o = 2V₁ +5V₂ -10V₃.

Dec.-14, Marks 6

Solution : In the first step, design adder to get 2V₁ +5V₂

The circuit is shown in the Fig. 2.28.5 (a).

Generate 10 V₃ using inverting amplifier.

Then use subtractor to get V_o = V_o2 – V_o1

Use all resistances same for subtractor as 10 kΩ

Review Questions

1. Explain the differential amplifier using op amp.

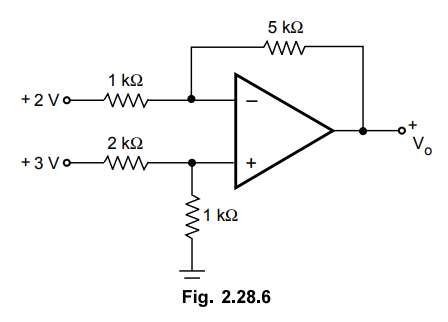
2. Calculate the output of the circuit shown in Fig. 2.28.6.

May-06, Marks 8

3. Draw an adder-subtractor type of circuit with op-amp to obtain the relation V₀ = (V₁ + V₂)- (V₃+ V₄).