Op-amp Summer or Adder Circuit

Summer or Adder Circuit

As the input impedance of an op-amp is extremely large, more than one input signal can be applied to the inverting amplifier. Such circuit gives the addition of the applied signals at the output. Hence it is called summer or adder circuit. Depending upon the sign of the output, the summer circuits are classified as inverting summer and non-inverting summer.

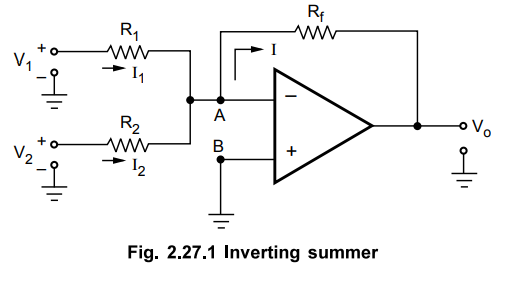
1. Inverting Summer

In this circuit, all the input signals to be added are applied to the inverting input terminal of the op-amp. The circuit with two input signals is shown in the Fig. 2.27.1.

As point B is grounded, due to virtual ground concept the node A is also at virtual ground potential.

V_A = 0 .... (2.27.1)

Now from the input side,

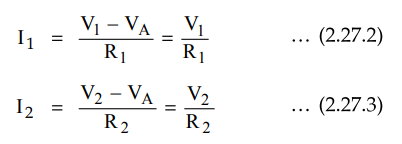
Applying KCL at node A and as input op-amp current is zero,

I = I₁ + I₂ ….. (2.27.4)

From the output side,

I = V_A – V_o / R_f = - V_o / R_f  …. (2.27.5)

Substituting equations (2.27.5), (2.27.2) and (2.27.3) in equation (2.27.4),

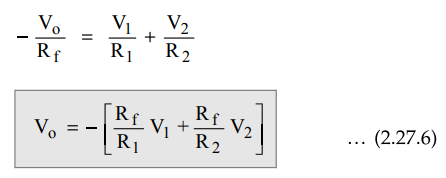
If the three resistances are equal, R₁ = R₂ = R_f

V_o = - ( V₁ + V₂ )   …. (2.27.7)

By properly selecting R_f, R₁ and R₂, we can have weighted addition of the input signals like aVf + bV2, as indicated by the equation (2.27.6).

Infact in such a way, n input voltages can be added.

Key Point Thus the magnitude of the ouput voltage is the sum of the input voltages and hence circuit is called summer or adder circuit.

2. Non-inverting Summing Amplifier

The circuit discussed above is inverting summing amplifier, which can be noticed from the negative sign in the equation (2.27.6). But a summer that gives non-inverted sum of the input signals is called non-inverting summing amplifier. The circuit is shown in the Fig. 2.27.2

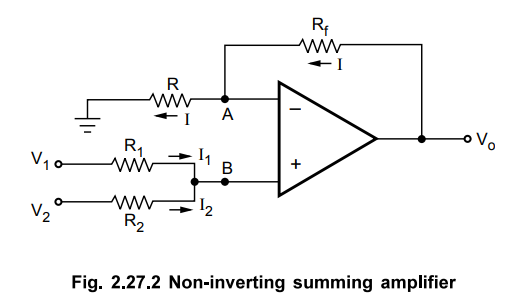
Let the voltage of node B is V_B. NOW the node A is at the same potential as that of B, due to virtual ground.

V_A = V_B  …. (2.27.8)

The equation (2.27.15) shows that the output is weighted sum of the inputs.

If R₁ = R₂ = R = R_f, we get

V_o = V₁ + V₂   …. (2.27.16)

Key Point As there is no phase difference between input and output, it is called non-inverting summer amplifier.

3. Average Circuit

If in the inverting summer circuit, the values of resistance are selected as,

R₁ = R₂ = R

and  R_f = R / 2

Then from the equation (2.27.6) we get,

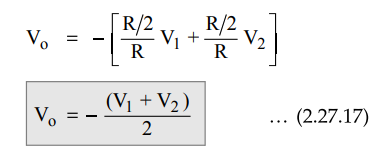
Key Point Thus the magnitude of the output voltage is the average of the two input voltages. So circuit acts like an averager.

Similarly average of n inputs can be calculated by selecting,

R₁ = R₂ = R₃ = ... = R_n = R and R_f = R / n

Example 2.27.1 Determine the output voltage for the following circuit.

Solution : This the an inverting summing amplifier.

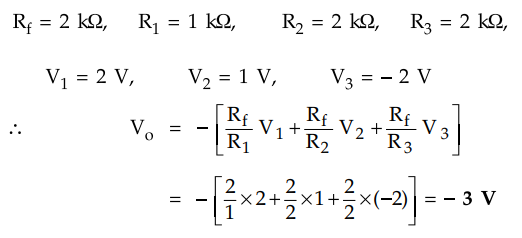
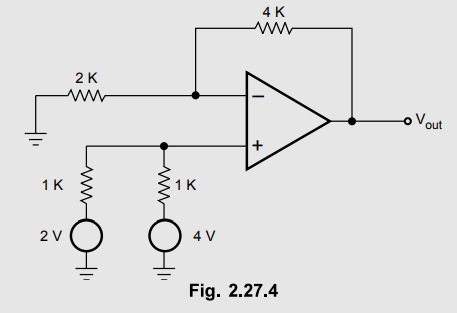
Example 2.27.2 Determine the output voltage for the circuit shown in Fig. 2.27.4.

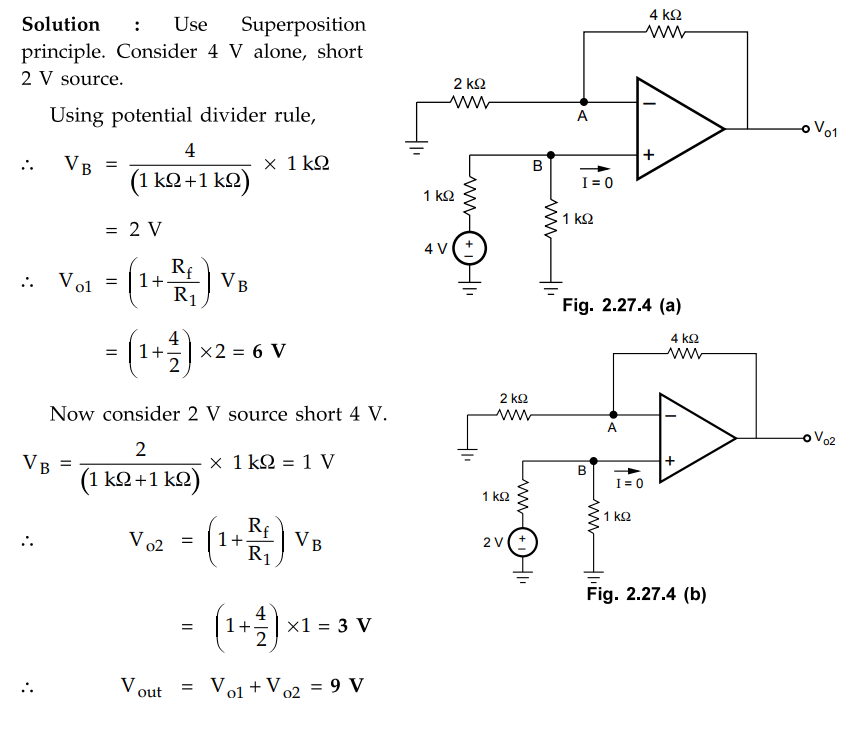
Solution : Use Superposition principle. Consider 4 V alone, short 2 V source.

Using potential divider rule,

Example 2.27.3 Draw an adder circuit for the given expression V_o = -(0.1 V₁ + V₂ +5V₃)

Dec.-l0, Marks 8

Solution :

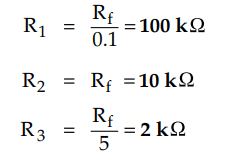
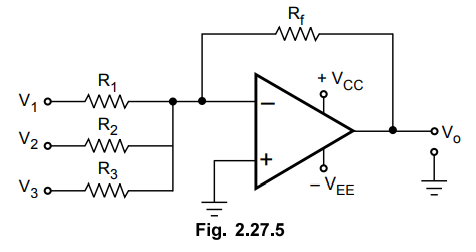
The adder circuit is shown in the Fig. 2.27.5.

Review Questions

1. Draw and explain the summing amplifier.

2. Explain how the average circuit can be derived from the summer.

Dec.-09, Marks 2

3. Determine the output voltage for the configuration shown in the Fig. 2.27.6.

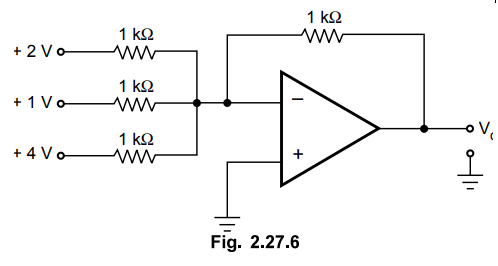
[ Ans.: - 7 V ]

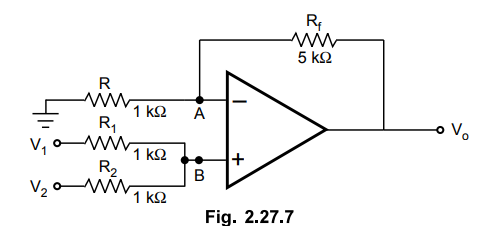
4. Determine the output voltage for the circuit shown in the Fig. 2.27.7, for V₁ = 1 V and V₂ = 3 V.

 [ Ans.: 12 V ]

5. Calculate the value of Rs in the Fig. 2.27.8 shown, such that V_o becomes zero.

[Ans.: 6.285 kΩ]