Op-amp Voltage to Current Converter

Voltage to Current Converter

In a voltage to current converter, the output load current is proportional to the input voltage. According to the connection of load there are two types of V to I converters : Floating type and Grounded type. In floating type V to I converter RL is not connected to the ground whereas in grounded type, one end of R_L is connected to the ground.

1. Voltage to Current Converter with Floating Load

The Fig. 2.25.1 shows a voltage to current converter in which load resistor R_L is floating.

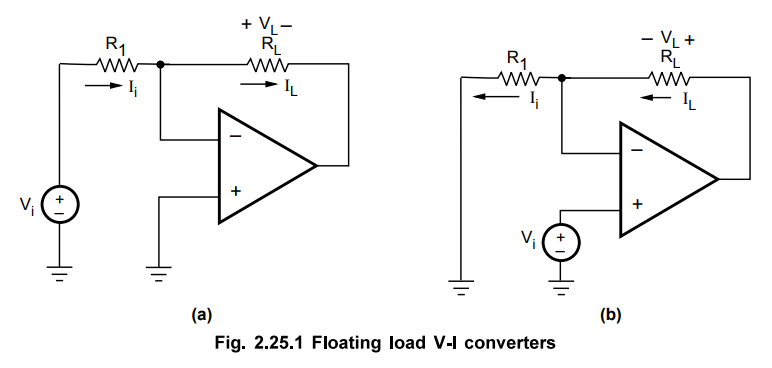
As input current of op-amp is zero.

I_L = I_i – V_i / R₁ … (2.25.1)

I_L ∝ V_i   … (2.25.2)

Key Point Thus the load current is always proportional to the input voltage and circuit works as voltage to current converter.

If the load is a capacitor, it will charge or discharge at a constant rate. Hence such converter circuits are used to generate the sawtooth or triangular waveforms. The proportionality constant is generally 1/R₁ hence this circuit is also called transconductance amplifier It is also called a Voltage Controlled Current Source (VCCS).

The expression I_L = V_i/R₁ holds regardless of the type of the load. It can be linear (e.g., a resistive) or non-linear (e.g., a light emitting diode), or it can have time-dependent characteristics (e.g., a capacitor). No matter what the load is, the op-amp will draw the current Ii whose magnitude depends only on V_i and R.

2. Voltage to Current Converter with Grounded Load

When one of end of the load is grounded, it is no longer possible to place the load within feedback loop of the op-amp. Fig. 2.25.2 shows a voltage to current converter in which one end of load resistor R_L is grounded. It is also known as 'Howland Current Converter' from the name of its inventor.

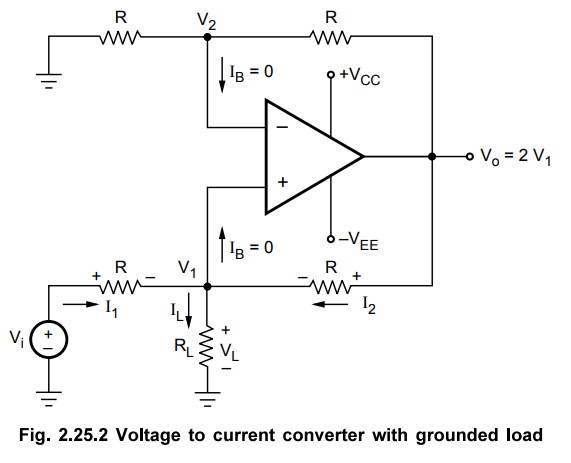
The analysis of the circuit is accomplished by first determining the voltage Vi at the non-inverting input terminal and then establishing the relationship between V₁ and the load current.

Applying KCL at node V₁ we get, I₁ +I₂ = I_L

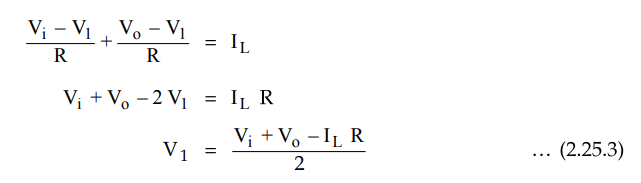
The gain of op-amp in non-inverting mode is given as A = 1 + R_f/R₁ For this circuit it is 1 + R/R = 2. Hence, output voltage can be written as,

From the above equation we can say that the load current depends on the input voltage V_i and resistor R.

3. Applications of V-I Converter

a. Low Voltage D.C. Voltmeter

The V-I converter circuit with floating load can be modified as a low voltage d.c. voltmeter circuit. The resistance R_L is to be replaced by D'Arsonval meter movement. This is shown in the Fig. 2.25.3.

For accurate readings it is necessary to make the nulling of op-amp. This is done by offset voltage compensating network. Let R_m be the meter resistance. The effective Thevenin's equivalent of compensating network is 10 Ω. Hence when switch S is in position 1, the effective R₁ is 1 kΩ + 10Ω ≈ 1 kΩ.

So current of 1 mA i.e. input of 1 V will result full scale deflection, if meter has full scale deflection current of 1 mA.

When switch is in position 2 then Ri = 5 kΩ. Thus for full scale deflection,

Thus 5 V are required to cause full scale deflection. Thus range of voltmeter increases by 5. Similarly at positions 3 and 4, ranges of X10 and X13 are also obtained.

Remember that for ±15 V supply, maximum input voltage range is ±14 V hence with ±15 V supply, maximum range possible is X13.

It is important to note that meter resistance R_m does not affect the value of Io. Thus meter can be calibrated properly to measure d.c. voltages.

b. Low Voltage A.C. Voltmeter

To measure a.c. voltages, the full wave bridge rectifier is used and D'Arsonval meter movement is used. The combination of meter and rectifier is used in the feedback loop of a.c. voltmeter. The circuit is shown in the Fig. 2.25.4.

The alternating current Io is converted to d.c. During positive half cycle of Vin the diodes D3 and D4 conduct while for negative half cycle of Vin the diodes D1 and D2 conduct. The direction of current through meter is always same for both the half cycles of Vin. Thus meter gives the average (d.c.) value of the rectified current. If it is necessary to calibrate the meter interms of r.m.s. values of input voltage then the factor 1.11 must be considered which relates r.m.s. and average values for purely sinusoidal waveforms. The range can be extended using the selector switch S and various resistances as shown in the Fig. 2.25.4. At position 2, X2 can be obtained. At position 3, X5 range can be obtained. At positition 4, X10 range can be obtained. It must be noted that due to low slew rate of 741 op-amp, the input a.c. voltage frequency should not be greater than 4 kHz. Similarly PIV ratings of the diodes must be large than the saturation voltages of op-amp. 

c. Diode Tester and Match Finder

Another application of V-I converter is a diode tester and diode match finder. The resistance R_L is replaced by a diode  as shown in the Fig. 2.25.5.

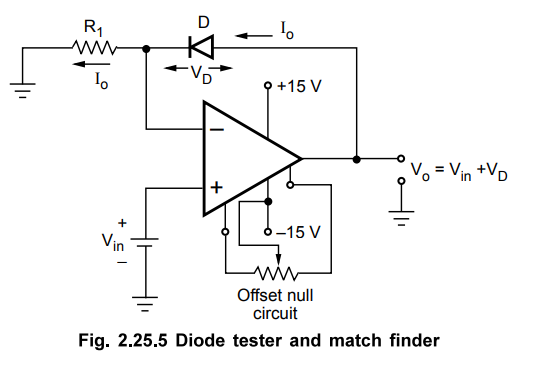
The current I_o is set by V_in and resistance R₁.

I_o = V_in  / R₁

So as long as V_in and R₁ are constants, the current I_o is also constant. The drop across diode can be directly measured by the voltmeter or the output voltage will be V_o = V_in + V_D From the value of V_D, the diode can be judged for its performance. Note that to avoid error in the output voltage, op-amp should be initially nulled using offset null circuit. 

Similarly replacing diodes one after the other, the perfectly matched diodes can be found out. R₁ can be selected according to V_in and testing current I_o required in the circuit.

The V-I converter circuit can also be used to test zener diode. The zener diode is connected in reverse biased condition in the feedback path as shown in the Fig. 2.25.6.

The current I_o is set by V_in and R₁.

If this current is more than knee current of the zener then voltage across zener is V_Z for which it is rated. Similarly matched zeners also can be obtained using same circuit.

The same circuit can be used for LED testing and match finding by replacing the feedback path by LED under test. The brightness of LEDS can be tested by setting specific current using V_in and R₁.

In all the applications, as 741 is used it is necessary to note that short circuit current rating of op-amp i.e. 25 mA should not be exceeded by the current I_o.

Example 2.25.1 For a V-I convertor shown in Fig. 2.25.7, V_in - 5 V, R - 10 k Ω, V₁ =1V, find the load current and output voltage V_o. Assume the op-amp is initially nulled.

Dec.-14, Marks 6 

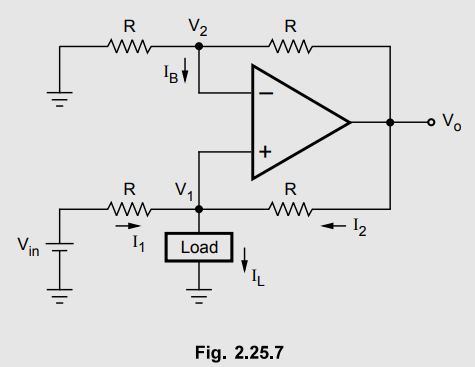
Solution: Assume I_B = 0 A.

The gain of the op-amp circuit in non inverting mode is A = 1 + R/R = 2.

V_o = 2V₁ = 2 × 1 = 2 V

Using in equation (1),  5 + 2 – 2 / 10×10³ = I_L

i.e. I_L = 0.5 mA

Review Questions

1. Draw and explain the circuit of a voltage to current converter if the load is 1) Floating 2) Grounded.

May-04, 10, 12, Dec.-06, 08, 10, Marks 8

2. With the help of circuit diagram explain the operation of V to I converter and its applications.

Dec.-06, 07,11, May-13,15, 17, Marks 8