Parallel Combination of Resistors

COMBINATION OF RESISTORS

In a practical case we may have many resistors. We have to connect them for getting desired resistance. The resistors can be connected in the following three fashions.

(a) Series combination

(b) Parallel combination

(c) Series - parallel combination

Parallel Combination

If one end of all the resistors is joined to a common point and the other ends are joined to another common point, the combination is said to be parallel combination between two common points.

A voltage source is connected between the common points. Hence the currents flow through different resistors. The voltage across each resistor will be the same as the supply voltage. So, the current through each element can be found by applying ohm's law for each resistor separately. The current is inversely proportional to the resistance.

Let R₁, R₂ and R₃ be the three resistors connected between the two common terminals A and B. Let V be the voltage supplied between A and B. Refer the fig.1.10

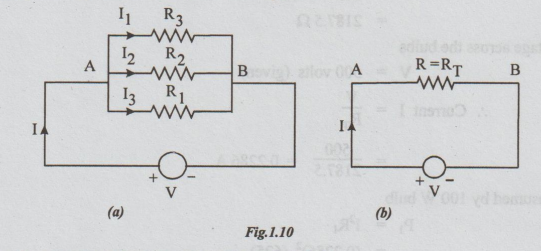
I₁, I₂ and I₃ are the currents through R₁, R₂ and R₃ respectively.

By ohm's law: I₁=V/R₁

I₂= V/R₂

I₃ = V/R₃

I = I_T = the total current = source current

Let R be the equivalent resistance of the combination

Refer figure 1.10(b). I = V / R

But I = I₁ + I₂ +1₃... (i)

Substituting the above expressions for the currents in equation (i), we get

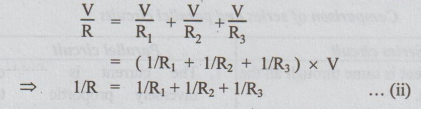
Hence, in the case of parallel combination the reciprocal of the equivalent resistance is equal to the sum of reciprocals of individual resistances.

Multiplying both sides of equation (ii) by V², we get

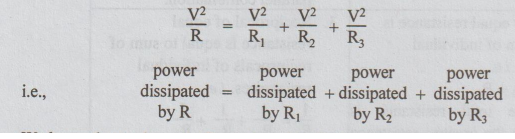
We know that reciprocal of resistance is called conductance.

i.e., conductance = 1/ Resistance

or  G = 1 / R

 The above equation (ii) can be written as

G = G₁ + G₂ + G₃

Important points in Parallel combination of resistors

1. Voltage is same across all elements. In other words, if the voltage is same the combination is parallel combination.

2. The current through the various resistors are different. The current through resistor is inversely proportional to its resistance.

3. The total resistance of a parallel circuit is always lesser than the smallest of the resistances.

4. Powers are additive.

5. The source current is the sum of the branch currents.

6. Conductance's are additive.

Advantages of parallel circuits

1. The electrical appliances of different power ratings may be rated for the same voltage. For example, in a house tube lights, bulbs, fridge, fans, motor are all rated for 230 volts. But their power ratings are different. In such cases if they are all connected in parallel the performance of others will not be affected.

2. In case a break (open) occurs in any of the branch circuits it, will not affect the other branch circuits. It is advantage only.

Applications of parallel circuits

1. All electrical appliances are connected in parallel. Each one of them can be controlled individually with the help of a separate switch.

2. Electrical wiring in cinema Halls, auditoriums, house wiring etc.

Comparison of series and parallel circuits

WORKED EXAMPLES ON D.C. PARALLEL CIRCUITS

Example 1 In the circuit shown in fig, calculate

 (i) the current in other resistors.

(ii) the value of unknown resistance 'X'.

(iii) the equivalent resistance across A - B.

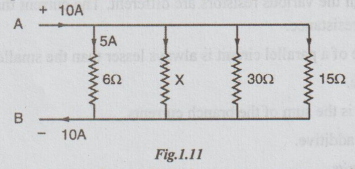
Solution: As all the resistors are in parallel, the voltage across each one is same. Given that current through 6Ω = 5A.

Voltage across 6 Ω = 5 × 6 = 30 volts [By Ohm's law]

Again, by Ohm's law, current through 30 Ω,

I30 = 30/30 = 1A

and current I15 = 30/15 = 2A

Given I6 = 5A

But I = I6 + Ix + I30 + I15 [By KCL]

⇒ 10 = 5 + Ix + 1 + 2

Ix = 2A

By applying ohm's law to x ohms resistor,

x = 30/Ix = 30/2 = 15 Ω

Let the equivalent resistance across AB = R

1/R = 1/6 + 1/x + 1/30 + 1/15

 = 1/6 + 1/15 + 1/30 + 1/15

= 5 + 2 + 1 + 1/30 = 1/3

R = 30 Ω

Ans: (i)Ix = 2A

I30= 1A

I15 =2A

(ii) X =15Ω

(iii)R=RAB = 3 Ω

Note: We can calculate R by applying ohm's law to the circuit shown above.

R = voltage / current = 30/10= 3 Ω

Example 2 Two resistors are connected in parallel and a voltage of 200 volts is applied to the terminals. The total current taken is 25A and the power dissipated in one of the resistors is 1500 W. What is the resistance of each element?

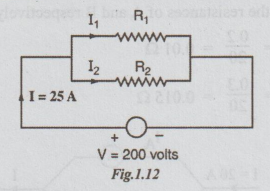
Solution:

V = 200 volts

I = 25A

Power dissipated by one resistor

(say) R1 = P1 = 1500 watts

But P1 =V2/R1

⇒R1 = V2/P1

Substituting the values, we get

Example 3 A current of 20A flows through two ammeters A and B joined in series. Across A, the p.d is 0.2 V and across B it is 0.3 V. Find how the same current will be divided between A and B when they are joined in parallel.

Solution: Let RA and RB be the resistances of A and B respectively.

By ohm's law,

RA  = 0.2/20 = 0.01 Ω

RB = 0.3/20 = 0.015 Ω

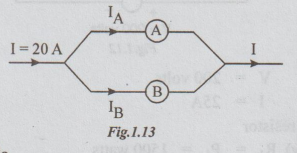
By division of current formula

IA = IRB /RA+RB = 20 × 0.015/0.01 + 0.015= 12A

But, by KCL, IA + IB = 1

⇒ IB = I - IA

= 20-12=8A

Ans:IA= 12A; IB = 8A

Example 4 Three resistors of 6 Ω, 9 Ω and 15 Ω are connected in parallel to a 180 V supply. Calculate (a) the current in each branch of the network. (b) the supply current (c) the total resistance of the network.

Solution:

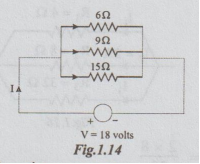
By ohm's law applied to each resistor, we get

I6 = 18/6=3A

I9 =18/9 = 2A

I15=18/15 =1.2A

Supply Current = Source Current

By KCL, ISource = Source Current

ISource = I6 + I9 + I15

= 3+2+1.2

= 6.2 A

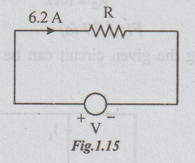
By Ohm's law,

Total resistance R = V/Isource

=18 / 6.2 Ω = 2.9 Ω

Answers: (i) I6 = 3A

I9 = 2A

I15 = 1.2 A

(ii) Isource =  6.2 A

(iii )R = 2.9 Ω

Example 5 A parallel network consists of three resistors of 4 Ω, 8 Ω and 32 Ω If the current in the 8 resistor is 2A, what are the currents in the other resistors?

Solution:

Since the resistors are connected in parallel, voltage across them is the same.

i.e., I2R2 =  I1R1 = I3R3 = V

I1 = I2 R2/ R1 = 2 × 8/4 = 4A

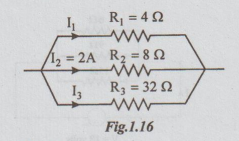
I3 = I2R2/R3 = 2 × 8/32

= 0.5A

Ans: I1 = 4A; I3 = 0.5 A

Example 6 Calculate the current supplied by the battery in the given circuit of the Fig1.17 (a).

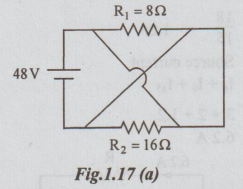
Solution: For easy understanding the given circuit can be re-drawn as shown in Fig.1.17 (b). There is no change in the connections.

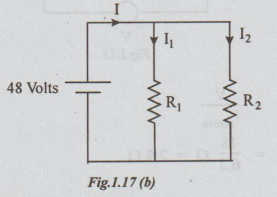
R1 and R2 are in parallel across the voltage of 48 volts.

The total resistance R = R1 R2 / R1 + R2

= 8 × 16 / 8 + 16 = 16/3  Ω

Equivalent circuit is

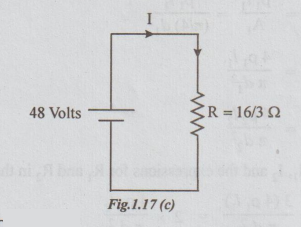
 Current from battery by Ohm's law,

I = V / R = 48 /16/3 = 9A

Note: From Fig.(b), by applying ohm's law to R1 and R2, we get I1 and I2

I1 = V/ R1 = 48/8 = 6A

and I2 = R2 = 48/16 = 3A

 I = I1 + I2

= 6+3 = 9A

Example 7 An aluminium wire of 5 m length and 2 mm diameter is connected in parallel with a copper wire of 3m long. Total current is 5A and that in aluminium is 3A. Find the diameter of copper wire. The specific resistances of aluminium and copper are 2.6 μΩ⇒cm and 1.7 μΩcm respectively.

Solution: Data: Use suffix 1 for aluminium and suffix 2 for copper.

l1 = 5m = 500cm

d1 = 2mm = 0.2cm

l2 = 3m = 300cm

I = 5A

I1 = 3A

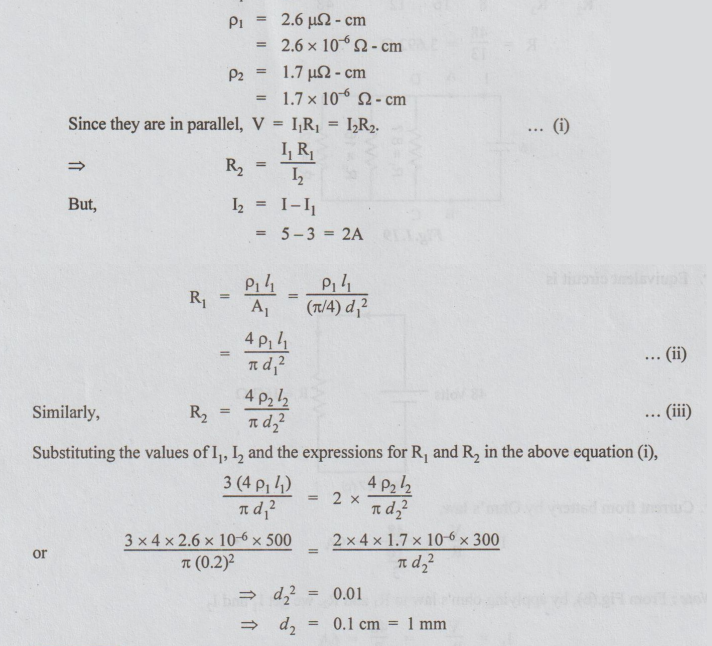
Example 8 Calculate the total resistance and battery current in the given circuit.

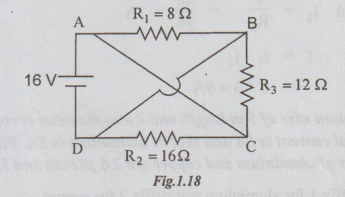
Solution: The given circuit is re-drawn as below. A and D are connected by wire of zero resistance. Hence they can be shown together similarly B and C can be shown as same terminal. Let R be the total resistance between A and B.

Then, R = R1 || R2 || R3

1/R =1/R1+1/R2+1/R3=1/8 +1/16 + 1/12 = 6+3+4/48

R = 48/13= 3.692Ω

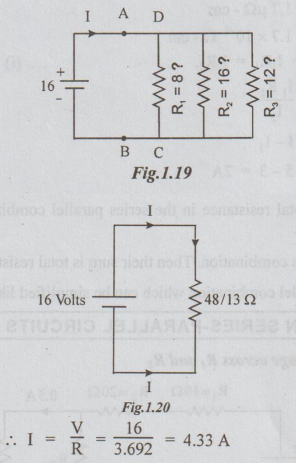
I = V/R = 16/3.692 = 4.33A

Ans: (i) R = 3.692 Ω (ii) I = 4.33 A

Note: We can find the currents I1, I2 and I3 by ohm's law. Then I and R can be calculated as shown below.

I1 = V/R1 = 16/8 = 2A

I2 = V/R2 = 16/16 = 1A

I3 = V/R3 = 16/12 = 1.33 A

By KCL, I = I1 + I2 + I3

= 2 + 1 + 1.33 = 4.33 A Ans.

And by Ohm's law, R = V/I = 16/4.333 = 3.692 Ω Ans.