Parallel Resonance Circuit

PARALLEL RESONANCE CIRCUIT

In parallel circuits, it is easier to analyse if the admittance is calculated. At resonance, the power factor being unity, reactive part of Z and reactive part of Y must be zero. Equating the reactive part of Y (admittance) to zero, we can get the expression for resonant frequency. At resonance the admittance is minimum and hence impedance is maximum. In other words, current is minimum.

1. Case (a): Resonance in Parallel RLC Circuit (Ideal Circuit)

Consider the parallel RLC circuit shown in the fig. 5.8.

For this ideal case the expression for resonant frequency seems to be same as that of series resonant frequency.

At resonance, the parallel RLC circuit behaves simply as resistance, the parallel LC combination known as a tank circuit behaves as an open circuit. But it does not mean that there is no current in the inductor and capacitor. The current actually circulates around the loop formed by the inductor and capacitor.

The quality factor Q = Ic (or) I_L / I at resonance = R / ω₀L CR ... (2)

2. Case (b): Resonance in a Parallel Practical Circuit

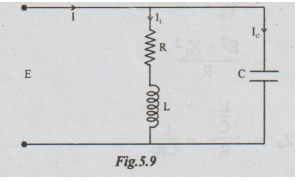
The admittance of the circuit = Y = Y_c + Y_L

= 1 / Z_c + 1 / Z_L

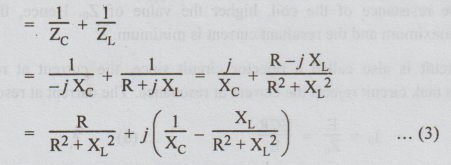
At resonance, the reactive part of Y must be zero.

At resonance, the admittance is denoted by Y₀.

From equation (3),

Z₀ is the dynamic impedance of the circuit. It is independent of frequency. The impedance is a pure resistance. Lower the resistance of the coil, higher the value of Z₀. Hence, the value of impedance at resonance is maximum and the resultant current is minimum.

A parallel resonant circuit is also called a rejector circuit since, the current at resonance is minimum. In other words, a tank circuit rejects the current at resonance. The current at resonance

= I₀ = E/Z₀ = ECR/L … (8)

This current is minimum current.

Effects of parallel resonance

For the circuit shown, at resonance,

(a) Impedance = L / CR. It is purely resistive.

(b) As L/C is very large, at resonance the impedance Z_r is very high.

(c) The circuit current is very small.

As a parallel resonant circuit draws a very small current and power from the mains, it is often regarded as rejector circuit.

Current Magnification

At resonance, in a parallel circuit, the branch current may be many times greater than the supply current. By means of a parallel resonance circuit, the current taken from supply can be greatly magnified. Hence, this type of resonance is called current resonance.

Current magnification = Ic / I = ω₀L / R = Q factor of the circuit

Thus Q factor is a measure of current magnification in a parallel resonant circuit.

3. Case (c): Parallel Resonance

 (Two branch circuit, one branch consisting of R-L and another of R - C.)

Note: From equation (4), the following observations can be made

(i) If R₁ = R₂, ω₀ = 1/√LC

(ii) If both R₁² and R₂² are greater or less than L/C simultaneously, a real value of is ω₀ obtained.

(iii) If R₁ R = R₂ = √L/C then the value of ω₀ is indeterminate.

i.e., resonance occurs at all frequencies. i.e., the circuit is purely resistive.

In this case impedance is a constant = √L/C

(iv) If R₁² < L/C and

R²₂  > L/C or vice versa, ω₀ is imaginary.

i.e., the circuit is never resonant.

(v) To find impedance at R₁ = R₂, put R₁ = R₂ = √L/C and

ω₀ = 1/√L/C then Y = -√C/L

Z = 1/Y = √L/C

COMPARISON OF SERIES AND PARALLEL RESONANT CIRCUITS 

(PRACTICAL PARALLEL RESONANT CIRCUIT IS CONSIDERED)