Performance Analysis of Short Transmission Lines

Performance Analysis of Short Transmission Lines

The equivalent circuit for a short transmission line is represented in the Fig. 2.5.1. In the analysis of short transmission lines, the capacitive effects are small and neglected. The resistance and inductance of the line are only taken into consideration. These parameters are taken to be lumped instead of distributed for the analysis. The circuit then simplifies to a simple a.c. series circuit as shown in the Fig. 2.5.1.

AU: May-17, Dec.-17

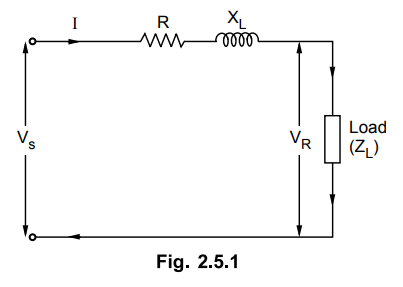
Let

I = Load Current

R = Resistance of the loop i.e. resistance of both conductors

X_L = Inductive loop reactance

V_R = Receiving end voltage, cos ϕ_R = Receiving end power factor

V_S = Sending end voltage, cos ϕ_S Sending end power factor

Z_L = Load impedance

The corresponding phasor diagram is shown in the Fig. 2.5.2 for lagging load power factor.

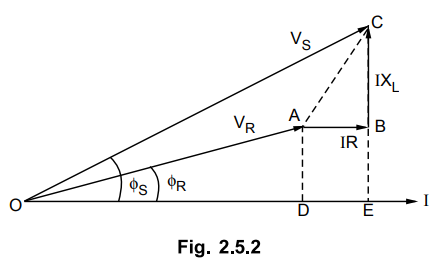
From the right angled triangle OEC we have,

The approximate expression for sending end voltage Vs can be obtained as follows. Draw the perpendicular from B and C on OA produced which is shown in the Fig. 2.5.3. 

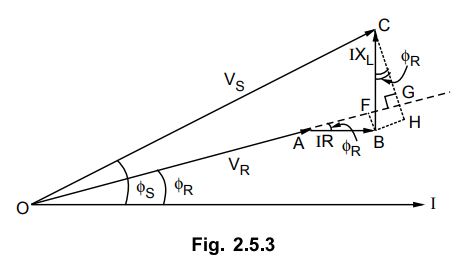
By making this adjustment we can see that OC = OG.

Use of complex notation :

Many a times it is convinient to make the analysis of line in complex notation. The phasor diagram is shown in the Fig. 2.5.4.

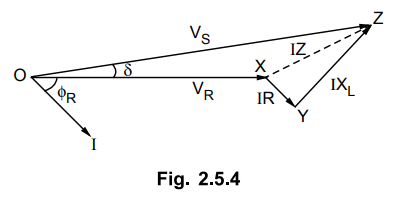
It can be seen that the second term in the above equation is very small and can be neglected without losing much accuracy. Therefore approximate expression for V_S is

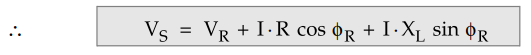
The important point to be noted that the approximate formula for Vs gives more accurate results for lagging power factors. But appriciable error is seen in case of leading  power factors. Hence this expression for Vg is to be applied to the loads having lagging power factors.

Example 2.5.1 A single phase 50 Hz generator supplies an inductive load of 6 MW at 0.8 pf lagging by means of an overhead line 15 km long. The line resistance and inductance are 0.02 ohm/km and 0.85 mH/km. The voltage at the receiving end is 11 kV. Determine the sending end voltage and voltage regulation.

Solution :

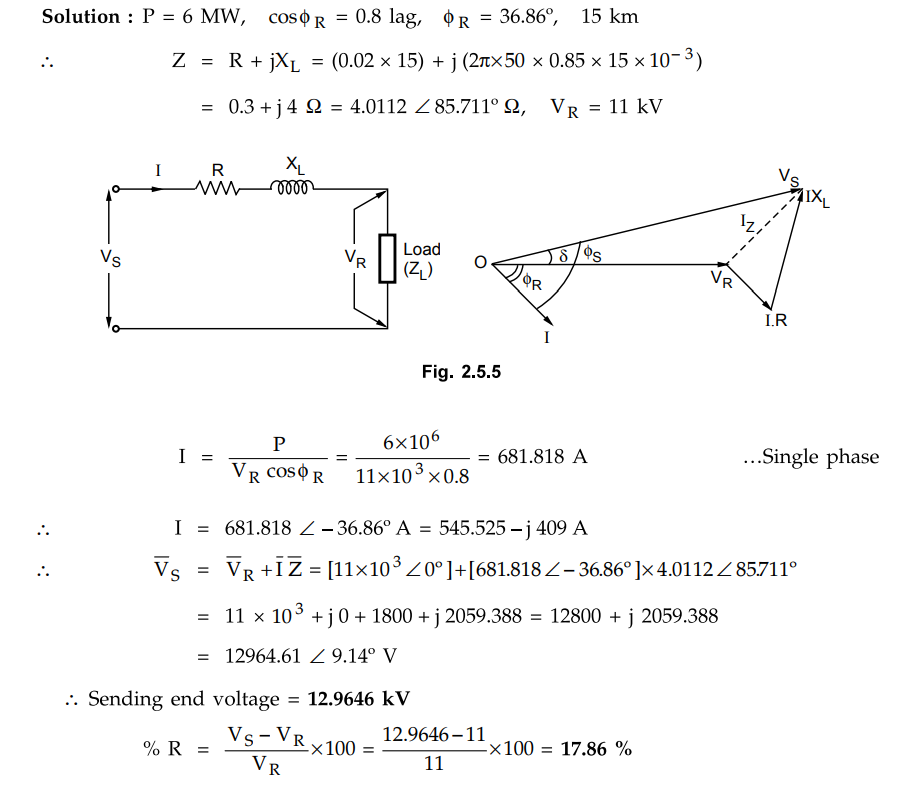
Review Question

1. Deduce an expression for voltage regulation and transmission efficiency of a single phase short transmission line, giving the vector diagram.