Phasor Diagram of a Loaded Alternator

Phasor Diagram of a Loaded Alternator

The above voltage equation is to be realised using phasor diagrams for various load power factor conditions. For drawing the phasor diagram consider all per phase values and remember following steps.

Steps to draw the phasor diagram :

1. Choose current Ia as a reference phasor.

2. Now if load power factor is cos ty , it indicates that angle between V_ph and Ia is ty as V_ph is the voltage available to the load.

So show the phasor V_ph m such a way that angle between V_ph and I_a is ϕ . For lagging ϕ’, I_a should lag V_ph and for leading ϕ', I_a should lead V_ph- For unity power factor load ϕ is zero, so V_ph and I_a are in phase.

3. Now the drop I_aR_a is a resistive drop and hence will always be in phase with I_a. So phasor I_a R_a direction will be always same as I_a, i.e. parallel to I_a. But as it is to be added to V_ph, I_a R_a  phasor must be drawn from the tip of the V_ph phasor drawn.

4. The drop IaXs is drop across purely inductive reactance. In pure inductance, current lags voltage by 90°. So ’I _aX_s' phasor direction will be always such that Ia will lag I_aX_s phasor by 90°. But this phasor is to be drawn from the tip of the I_aR_a phasor to complete phasor addition of V_ph,I_aR_a and I_aX_s

5. Joining the starting point to the terminating point, we get the phasor E_ph. Whatever may be the load power factor, I_a R_a is a resistive drop, will be in phase with Ia while I_aX_s is purely inductive drop and hence will be perpendicular to I_a in such a way that I_a will lag I_aX_s by 90°. This is shown in the Fig. 2.9.1.

By using the above steps, the phasor diagrams conditions can be drawn.

1. Lagging Power Factor Load

The power factor of the load is cos ϕ lagging so I_a lags V_ph by angle ϕ. By using steps discussed above, phasor diagram can be drawn as shown in the Fig. 2.9.2.

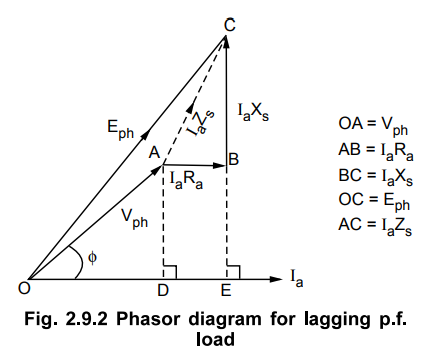
To derive the relationship between E_ph and V_ph, the perpendiculars are drawn on the current phasor from points A and B. These intersect current phasor at points D and E respectively.

Now, OD = V_ph cos ϕ

AD = BE = V_ph sin ϕ

DE = I_aR_a

Consider ∆ OCE, for which we can write,

(OC)² = (OE) ² + (EC) ²

(Eph) ² = (OD + DE) ² + (EB + BC) ²

(Eph) ² = (V_ph cos ϕ + I_aR_a)² + (V_ph sinϕ + I_aX_s)²

From this equation, the value of induced e.m.f. can be calculated. 

2. Leading Power Factor Load

The power factor of the load is cos ϕ leading. So I_a leads V_ph by an angle ϕ . By using steps discussed, the phasor diagram can be drawn as shown in the Fig. 2.9.3.

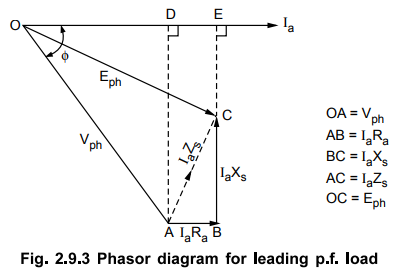
To derive the relation between E_ph and V_ph, the perpendiculars are drawn on current phasor from points A and B. These intersect current phasor at points D and E respectively.

From ∆ OAD, OD = V_ph cos ϕ

AD = BE = V_ph sin ϕ

DE = I_aR_a

Consider ∆ OCE, for which we can write,

(OC)² = (OE) ² + (EC) ²

(Eph ) ² = (OD + DE) ² + (BE - BC) ²

(Eph) ² = (V_ph cos ϕ + I_aR_a) ² + (V_ph   sin ϕ I_aX_s) ²

It can be observed that the sign of the I_aX_s is negative as against its positive sign for lagging p.f. load. This is because X₅ consists of X_ar. i.e. armature reaction reactance. Armature reaction is demagnetising for lagging while magnetising for leading power factor loads. So sign of I_aX_s is opposite for lagging and leading p.f conditions.

3. Unity Power Factor Load

The power factor of the load is unity i.e. cos ϕ = 1. So ϕ = 0, which means V_ph is in phase with I_a. So phasor diagram can be drawn as shown in the Fig. 2.9.4.

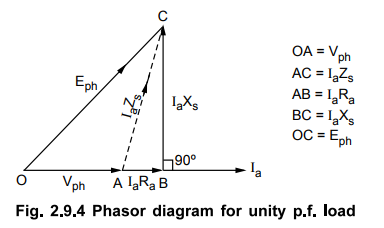
Consider ∆ OBC, for which we can write,

(OC)² = (OB)² + (BC)² 

(E_ph) ² - (OA + AB) ² + (BC) ²

(E_ph) ² = (V_ph + I_aR_a) ² + (I_aX_s) ²

As cos ϕ = 1, so sin ϕ = 0 hence does not appear in the equation.

Note : The phasor diagrams can be drawn by considering voltage Vph as a reference phasor. But to derive the relationship, current phasor selected as a reference makes the derivation much more simplified. Hence current is selected as a reference phasor.

It is clear from the phasor diagram that V_ph is less than E_ph for lagging and unity p.f. conditions due to demagnetising and cross magnetising effects of armature reaction. While V_ph is more than E_ph for leading p.f. condition due to the magnetising effect of armature reaction.

Thus in general for any power factor condition,

(E_ph)² = (V_ph cosI_aR_a)2 + (V_ph sinI_aX_a)²

+ Sign for lagging p.f. loads

- Sign for leading p.f. loads

and    V_ph = Per phase rated terminal voltage

I_a = Per phase full load armature current

From this discussion, we can now define the voltage regulation of an alternator

The angle between E_ph and V_ph is called load angle and denoted as δ.

Review Questions

1. Draw the vector diagram of an alternator supplying lagging, leading and unity power factor load and hence derive an expression for the no load e.m.f. in terms of terminal voltage, load current, armature resistance and synchronous reactance.

2. Draw the vector diagrams of loaded alternator for lagging, leading and unity power factor conditions and explain them.