PLA (Programmable Logic Array)

PLA (Programmable Logic Array)

Dec.-05, 06, 08, 12, 16, 17, May-08, 09, 10, 11, 17

• The combinational circuit do not use all the minterms every time. Occasionally, they have don't care conditions. Don't care condition when implemented with a PROM becomes an address input that will never occur. The result is that not all the bit patterns available in the PROM are used, which may be considered a waste of available equipment.

• For cases where the number of don't care conditions is excessive, it is more economical to use a second type of LSI component called a Programmable Logic Array (PLA). A PLA is similar to a PROM in concept; however it does not provide full decoding of the variables and does not generates all the minterms as in the PROM. The PLA replaces decoder by group of AND gates, each of which can be programmed to generate a product term of the input variables. 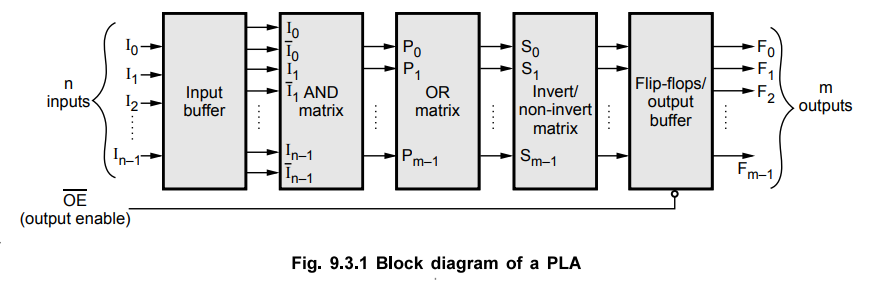In PLA, both AND and OR gates have fuses at the inputs, therefore in PLA both AND and OR gates are programmable. Fig. 6.6.17 shows the block diagram of PLA. It consists of n-inputs, output buffer with m outputs, m product terms, m sum terms, input and output buffers. The product terms constitute a group of m AND gates and the sum terms constitute a group of m OR gates, called OR matrix. Fuses are inserted between all n-inputs and their complement values to each of the AND gates. Fuses are also provided between the outputs of the AND gates and the inputs of the OR gates. The third set of fuses in the output inverters allows the output function to be generated either in the AND-OR form or in the AND-OR-INVERT form. When inverter is bypassed by link we get AND-OR implementation. To get AND-OR-INVERTER implementation inverter link has to be disconnected.

 

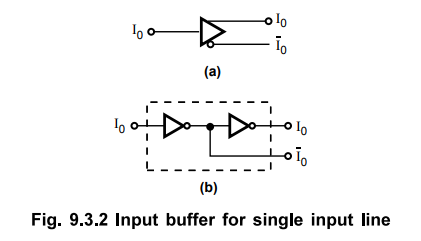
1. Input Buffer

• Input buffers are provided in the PLA to limit loading of the sources that drive the inputs. They also provide inverted and non-inverted form of inputs at its output. The Fig. 9.3.2 shows two ways of representing input buffer for single input.

 

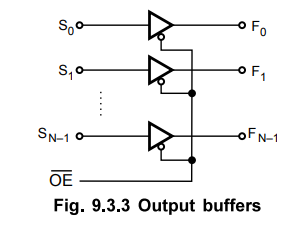
2. Output Buffer

The driving capacity of PLA is increased by providing buffers at the output. They are usually 1 IL compatible. The Fig. 9.3.3 shows the tri-state, 1 IL compatible output buffer. The output buffer may provide totem-pole, open collector or tri-state output.

 

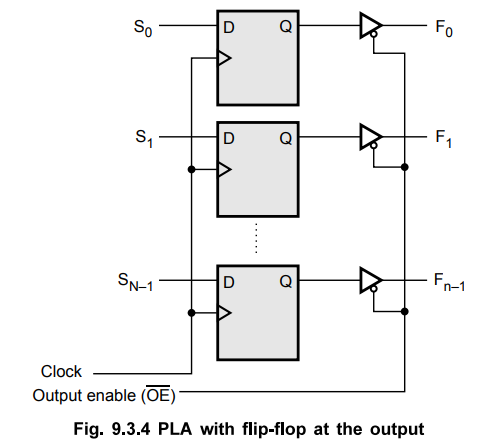
3. Output through Flip-Flops

For the implementation of sequential circuits we need memory elements, flip-flops and combinational circuitry for deriving the flip-flop inputs. To satisfy both the needs some PLAs are provided with flip-flop at each output, as shown in the Fig. 9.3.4.

 

4. Implementation of Combination Circuit using PLA

• Like ROM, PLA can be mask-programmable or field-programmable. With a mask-programmable PLA, the user must submit a PLA program table to the manufacturer. This table is used by the vendor to produce a user-made PLA that has the required internal paths between inputs and outputs. A second type of PLA available is called a field-programmable logic array or FPLA. The FPLA can be programmed by the user by means of certain recommended       procedures. FPLAs can be programmed with commercially available programmer units.

• As mentioned earlier, user has to submit PLA program table to the manufacturers to get the user-made PLA. Let us study how to determine PLA program table with the help of example.

 

Examples for Understanding

Ex. 9.3.1 A combinational circuit is defined by the functions :

F₁ = ∑ m (3,5,7), F₂ = ∑ m (4,5,7)

Implement the circuit with a PLA having 3 inputs, 3 product terms and two outputs.

Solution :

Step 1 : Simplify the given Boolean functions

The Boolean functions are simplified, as shown in the Fig. 9.3.5. The simplified functions in sum of products are obtained from the maps are :

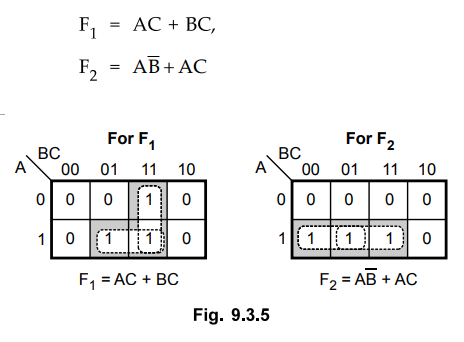
Step 2 : Write PLA program table

Therefore, there are three distinct product terms : AC, BC and AB, and two sum terms. The PLA program table shown in Table 9.3.1 consists of three columns specifying product terms, inputs and outputs. The first column gives the lists of product terms numerically. The second column specifies the required paths between inputs and AND gates. The third column specifies the required paths between the AND gates and the OR gates. Under each output variable, we write a T (for true) if the output inverter is to be bypassed, and C (for complement) if the function is to be complemented with the output inverter. The product terms listed on the left of first column are not the part of PLA program table they are included for reference only.

Step 3 : Implementation

 

Ex. 9.3.2 Draw a PLA circuit to implement the logic functions

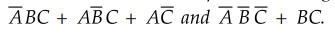
Sol. :

Step 1 : Simplify the Boolean functions

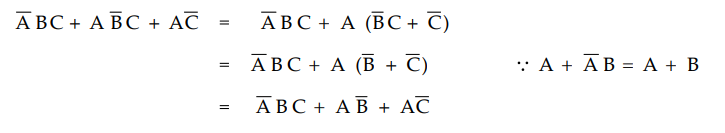
Note : The second Boolean function is in simplified form.

Step 2 : Implementation

 

Ex. 9.3.3 Implement the following multiboolean function using 3 × 4 × 2 PLA PLD.

f₁ (a₂, a₁, a₀ ) = ∑ m (0, 1, 3, 5) and

f₂ (a₂, a₁, a₀ ) = ∑ m (3, 5, 7)

Sol. :

Step 1 : Simplify the Boolean functions.

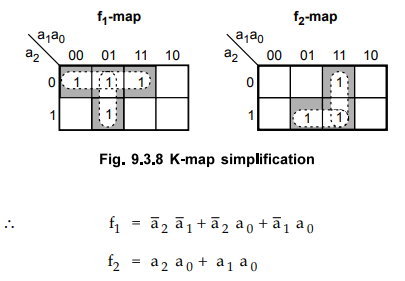
To implement functions fj. and f2 we require 3 x 5 x 2 PLA and we have to implement them using 3x4x2 PLA. Therefore, we have to examine product terms by grouping Os instead of 1. That is product terms for complement of a function.

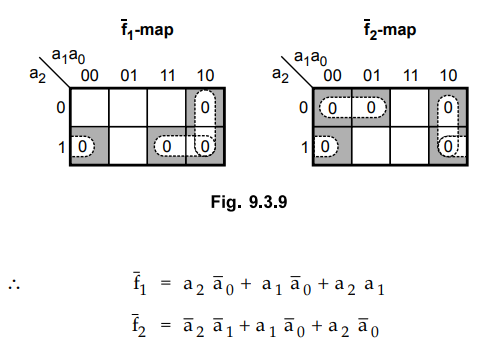
Step 2 : Implementation

Looking at function outputs we can realize that product terms 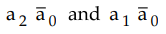 are common in both functions. Therefore, we need only 4 product terms and functions can be implemented using a 3 × 4 × 2 PLA as shown in Table 9.3.2 and Fig. 9.3.10.

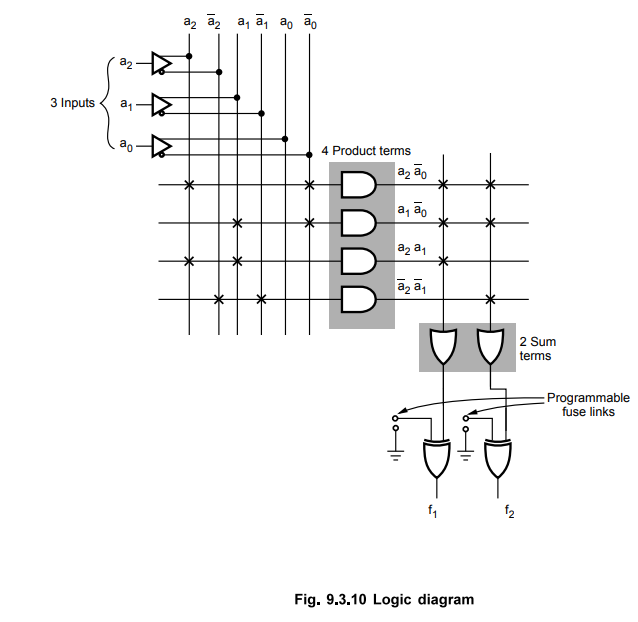
PLA

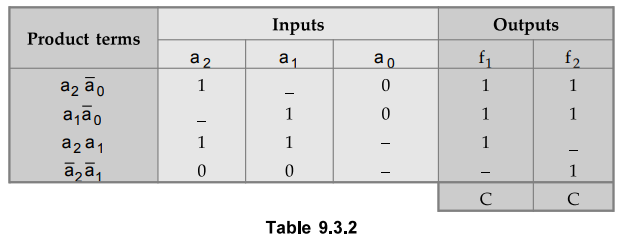
As shown in the Fig. 9.3.10 exclusive-OR gate is programmed to invert the function to get the desired function outputs.

 

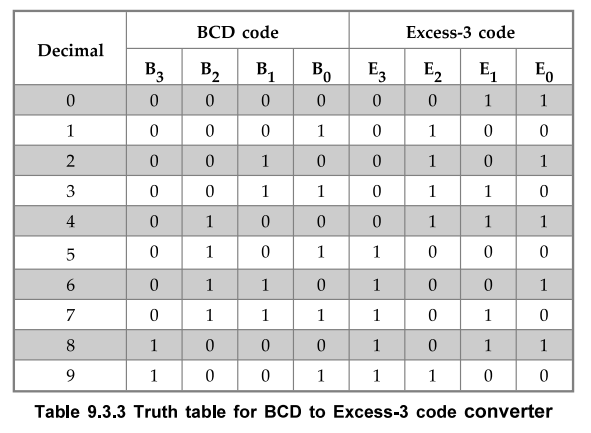
Ex. 9.3.4 Design a BCD to Excess-3 code converter and implement using suitable PLA.

Sol. :

Step 1 : Derive the truth table of BCD to Excess-3 converter

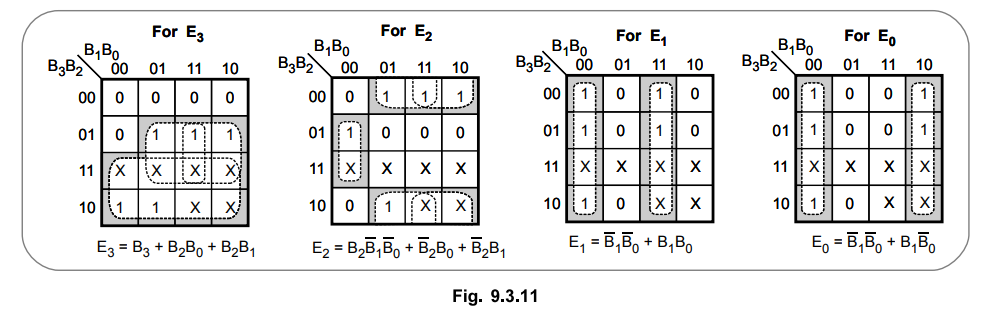
Step 2 : Simplify the Boolean functions for Excess-3 code

Step 3 : Write PLA program table

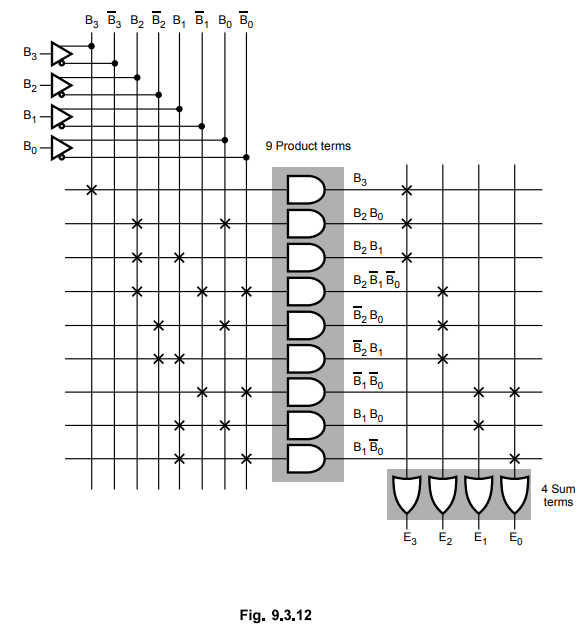
Step 4 : Implementation

 

Examples with Solutions

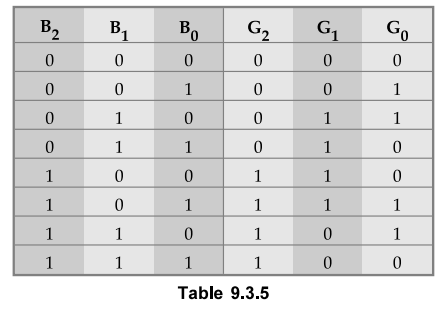
Ex. 9.3.5 Design and implement 3-bit binary to gray code converter using PLA. 

Sol. :

Step 1 : Derive the truth table for 3-bit binary to gray code converter

Step 2 : Simplify the Boolean functions for gray code

Step 3 : Implementation

 

 

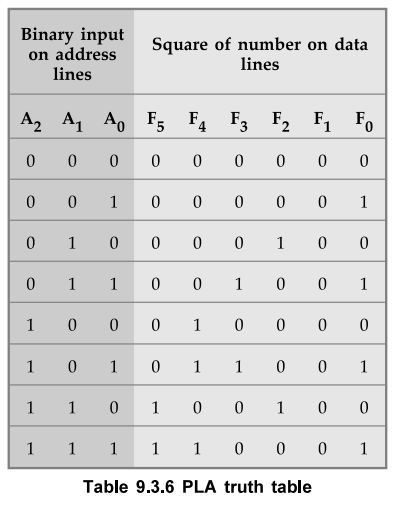
Ex. 9.3.6 Design a combinational circuit using PLA. The circuit accepts 3-bit number and generates an output binary number equal to square of input number. 

Sol . :

Step 1 : Derive the truth table

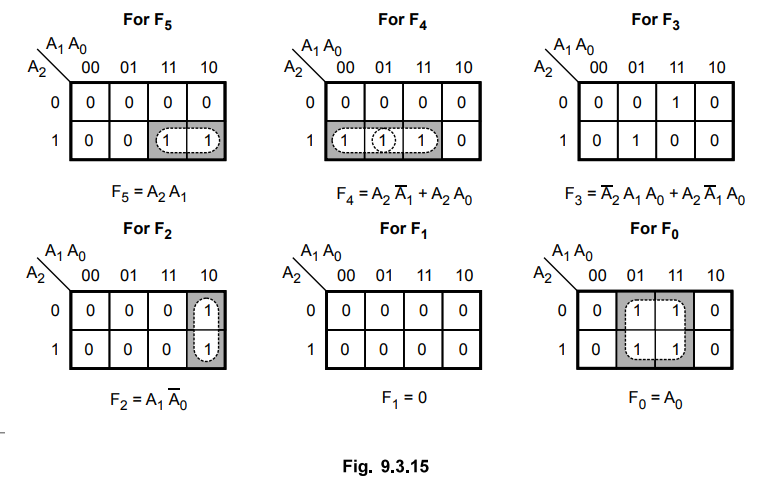
Step 2 : Simplify Boolean functions of square output

Step 3 : Implementation

 

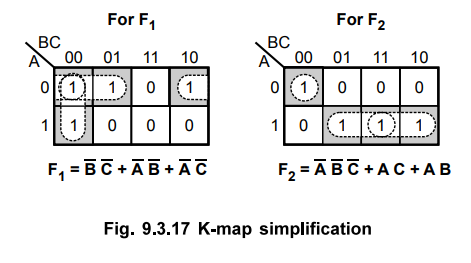
Ex. 9.3.7 Implement the following two Boolean functions with a PLA.

F₁ (A, B, C) = ∑ (0, 1, 2, 4)

F₂ (A, B, C) = ∑ (0, 5, 6, 7)

Sol . :

Step 1 : Simplify the Boolean function

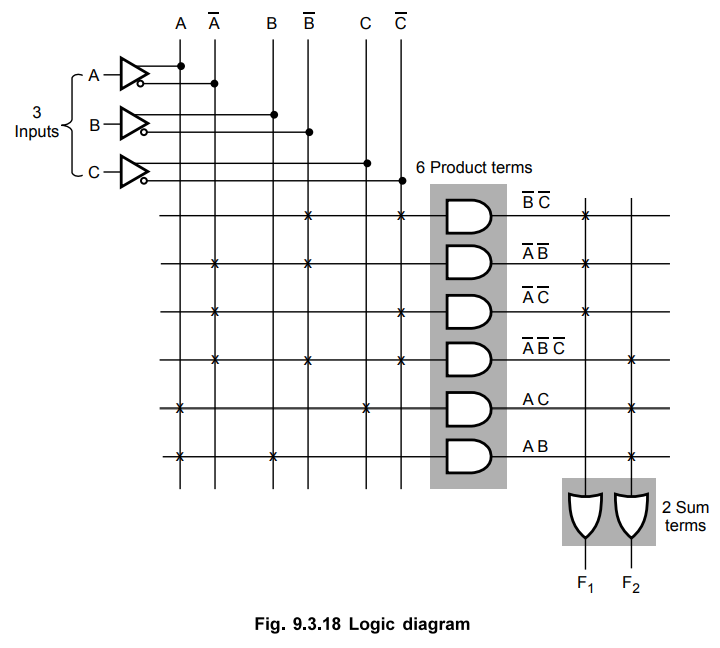
Step 2 : Implementation

 

Ex. 9.3.8 A combinational circuit is defined by functions.

F₁ (A, B, C) = ∑ (3, 5, 6, 7)

F₁ (A, B, C) = ∑ (0, 2, 4, 7).

Implement the circuit with a PLA having three inputs, four product terms and two outputs.

AU : Dec.-05, Marks 6

Sol . :

Step 1 : Simplify the Boolean functions

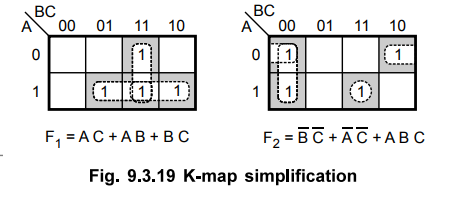
Here, we have 6 product terms so we check for complement functions.

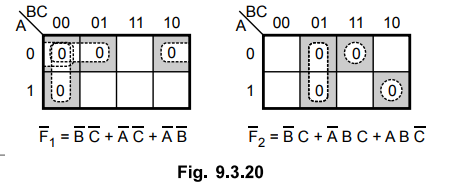
If we take 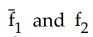 outputs of two functions, we need only four product terms since product terms 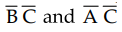 are common between them.

Step 2 : Implementation

 

Ex. 9.3.9 Design a PLA structure using AND and OR logic for the following functions.

F₁ = ∑m (0, 1, 2, 3, 4, 7, 8, 11,         12, 15)

F₂ = ∑m (2, 3, 6, 7, 8, 9, 12, 13)

F₃ = ∑m (1, 3, 7, 8, 11, 12, 15)

F₄ = ∑ m (0,         1, 4, 8, 11, 12, 15)

Sol. :

Step 1 : Simplify Boolean functions

AU : Dec.-16, Marks 10

Step : 2 Implementation

 

Examples for Practice

Ex. 9.3.10 Implement the following Boolean functions with a PLA

F₁ (A, B, C) = ∑ (0, 1, 2, 4)

F₂ (A, B, C) = ∑ (0, 5, 6, 7)

F₃  (A, B, C) = ∑ (0, 3, 5, 7).

Ex. 9.3.11 A combinational circuit is defined as the functions

F1 = AB’C’ + AB’C + ABC

F2 = A’BC + AB’C + ABC

Implement the digital circuit with a PLA having 3 inputs, 3 product terms, and 2 outputs.

Ex. 9.3.12 Draw a PLA circuit to implement the functions

F₁ = A'B + AC + ABC ; F₂ = (AC + AB + BC).

Ex. 9.3.13   Design and implement a 4-bit binary to Gray code converter using a PLA.

Ex. 9.3.14   Design an AND-OR-PLA that implements the functions

f(x, y, z) = ∑m (0, 2, 4, 6)

g(x, y, z) = ∑m (1, 3, 5, 7).

Review Questions

1. Discuss the concept, working and applications of PLA.

2. What is a PLA ?

3. How does the architecture of a PLA different from a PROM ?

AU : May-09, Marks 2