Point Form of Ampere's Circuital Law

Point Form of Ampere's Circuital Law

AU ; May-05, 16, Dec.-03, 07, 10

• In electrostatics, the Gauss's law is applied to the differential volume element to develope the concept of divergence. Similarly in magnetrostatics, the Ampere's circuit law is to be applied to the differential surface element to develope the concept of a curl.

• Consider the differential surface element having sides Δx and Δy plane, as shown in the Fig. 7.10.1. 

The unknown current has produced   at the centre of this incremental closed path.

• The total magnetic field intensity at the point P which is centre of the small rectangle is,

While the total current density is given by,

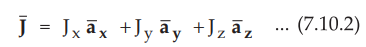
• To apply Ampere's circuit law to this closed path, let us evaluate the closed line integral of   about this path in the direction abcda. According to right hand thumb rule the current is in  direction.

• The intensity H_y along a-b can be expressed interms of H_y0 existing at P and the rate of change of H_y in the x direction with x. The distance in x direction of a-b from point P is (Δ x/2). Hence 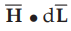  along a-b can be expressed as,

• Now H_x can be expressed interms of H_x0 at point P and rate of change of H_x in y direction with y.

H_x = H_x0 + Δy / 2 ∂H_x / ∂y

The distance of be from P is Δ y/2.

• But H_y can be expressed in terms of H_y0 and rate of change of H_y in negative x direction. The distance of cd from point P is (Ax/2) in negative x direction.

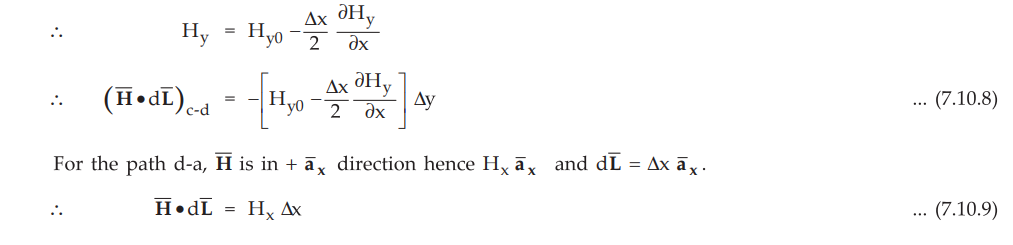
• But Hx can be expressed in terms of Hx0 and rate of change of Hx in negative x direction. The distance of cd from point P is (Ax/2) in negative y direction.

• According to Ampere's circuital law, this integral must be current enclosed by the differential element.

• Current enclosed = Current density normal to closed path × Area of the closed path

I_enc = J_z Δx Δy

• where Jz = Current density in direction as the current enclosed is in  direction.

• From equations (7.10.11) and (7.10.12) we can write,

• This gives accurate result as the closed path shrinks to a point i.e. Δx Δy area tends to zero.

• This equation gives relation between closed line integral of  per unit area and the current per unit area i.e. current density. To have equality sign between the two, the surface area of closed path must shrink to zero.

• Considering incremental closed path in yz plane we get the current density normal to it i.e. in x direction considering incremental closed path in zx plane we get the current density normal to it i.e. in y direction. So we can write,

• where JN = Current density normal to the surface ΔS.

• The term on left hand side of the equation is called curl . The ΔS_N is area enclosed by the closed line integral.

• The total  now can be obtained by adding (7.10.14), (7.10.15) and (7.10.16).

• The equation (7.10.18) is called the point form of Ampere's circuital law.

... This is one of the Maxwell's equations.

Key Point : The curl is not refering to any co-ordinate system though it is developed using cartesian co-ordinate system.

1. Curl in Various Co-ordinate Systems

• As the curl of  is a cross product it can be expressed in determinant form in various co-ordinate systems.

1. Cartesian co-ordinate system :

2. Cylindrical co-ordinate system :

Key Point : Note that in ∂ (rHϕ)  / ∂z constant as differentiation is with respect to z hence it becomes

r ∂Hϕ / ∂z But in ∂ (rHϕ)  / ∂r the r can not be taken out of differentiation, as differentiation is with respect to r.

3. Spherical co-ordinate system :

Ex. 7.10.1 A flat perfectly conducting surface in xy plane is situated in a magnetic field, 

Find the current density on the conductor surface.

Sol. : From the point form of Ampere's circuit law,

Ex. 7.10.2 Let 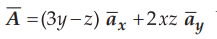Wb/m in a certain region of free space, a) Show that 

Sol. : The Ā is a vector magnetic potential.

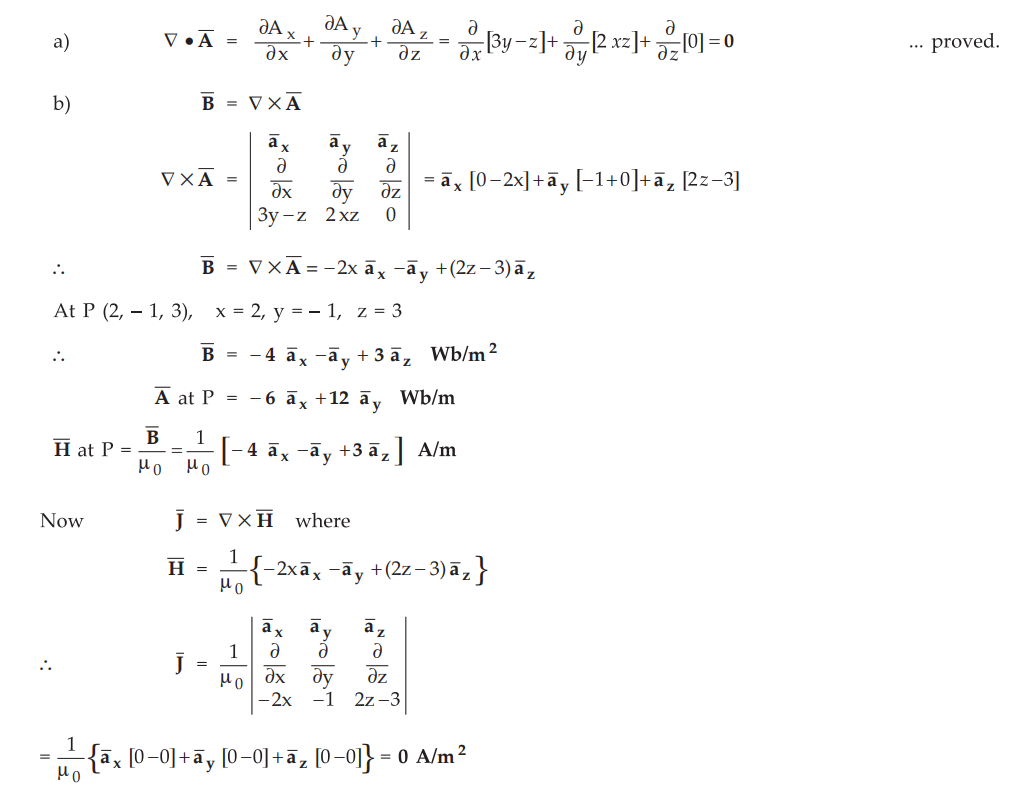
Review Questions

1. Deduce the point form of Ampere's circuital law.

AU : May-05, 16, Marks 8

2. Discuss about curl of a vector. Derive expression for curl of a vector.