Points to Remember

POINTS TO REMEMBER

1. Given the equation of v, the expression for i is found by the following way

 (a) for purely resistive circuit :

By Ohm's law, I V/ R

(b) for purely inductive circuit:

By integrating v.

(c) for purely capacitive circuit

By differentiating v.

2. For purely resistive circuit, if voltage and current are shown in the polar form, the angles of both must be same nature. For example if V = |V| ∠0. Then I = |1|∠0. If V= |V| Zπ/2. Then I = |I| ∠π/2 and so on.

3. The ratio of V to I is called impedance Z.

(a) For purely resistive circuit:

Z = R ∠0 in polar form

= R in rectangular form

 (b) For purely inductive circuit :

Z = X_L ∠π/2 in polar form

= jX_L in rectangular form.

(c) For purely capacitive circuit:

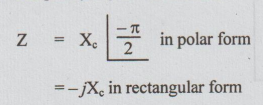
4. For purely resistive circuit, both V and I are in phase

Phase angle ϕ = 0

 cos ϕ = 1

In other words, if the power factor is unity, the circuit element is supposed to be purely resistive (Except resonant circuits).

5. For purely inductive circuit, current lags behind the voltage by π/2.

ϕ = π/2 radians, lag

cos ϕ =  сos π/2 = 0, lag

In other words, if the power factor of the circuit is zero lag, the circuit element is purely inductive.

6. For purely capacitive circuit, the current leads the voltage by. π/2

i.e.; ϕ = π/2 radians, lead.

⇒ cos ϕ =  0, lead.

Thus if the power factor of a circuit is zero lead, then the circuit element is purely capacitive.

7. The average power for pure

(a) resistive circuit = | V | | I |

(b) inductive circuit = 0

(c) capacitive circuit = 0

8. In polar form, for resistive circuit,

V = |V| ∠ 0 and I = |I| ∠ 0

9.For inductive circuit, if V is taken as reference,

V = | V | ∠0, I = |I| ∠ -π/2

10. For capacitive circuit with V as reference,

V = |V| ∠ 0, then, I = |I| ∠ π/2

It is to say that I leads V by π/2. It is as good as telling that V lags behind I by angle. π/2

But here also we have to prefer to say as how I is with reference to V.

If I is taken as reference then I= |I| ∠0, v = |v| ∠-π/2

11. In a circuit, if current lags behind the voltage by π/2 radians, then the circuit element must be purely inductive.

12. If the current leads the voltage by π/2 radians, then the circuit element must be purely capacitive.

13. (a) R is independent of frequency.

(b) X_L varies linearly with frequency.

(c) X_C varies inversely proportional to frequency.

14. The basic units of R, X_L and X_C are ohms.