Poisson distribution

POISSON DISTRIBUTION

The Poisson probability distribution was introduced by S.D. Poisson in a book he wrote regarding the application of probability theory to law suits, criminal trials, and the like.

1. Poisson Distribution

A random variable X is said to follow Poisson distribution if it assumes only non-negative values and its probability mass function is given by,

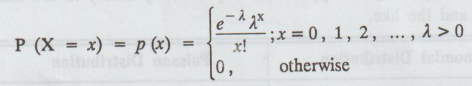
λ is known as the parameter of the Poisson distribution.

2. Poisson frequency distribution

Let a Poisson experimental consist of n independent trials. Let this experiment, under similar conditions be repeated N times. Then 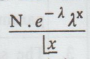 gives the expected number of x successes in N experiments, each consisting of n trials. The possible number of successes together with the expected frequencies is said to constitute a Poisson frequency distribution.

The following are some of the examples where the Poisson probability law can be applied :

1. Number of defective items produced in the factory

2. Number of deaths due to a rare disease.

3. Number of deaths due to the kick of a horse in an army.

4. Number of mistakes committed by a typist per page.

3. Additive property of Poisson random variables

If X₁ and X₂ are two independent Poisson random variable with parameters λ₁ and λ₂ then X₁ + X₂ is a Poisson random variable with parameter λ₁ + λ₂.

(i) No. of defective items produced

 (ii) No. of deaths due to a rare disease.

Note: The binomial distribution is characterised by two parameters p, n while the Poisson distribution is characterised by a single parameter λ. The sample space for the binomial distribution is {0, 1, 2, n} while the sample space for the poisson distribution is {0, 1, 2, n, ...} Expected value (mean) is given by λ and variance of the Poisson distribution is also λ.