Poisson's and Laplace's Equations

Poisson's and Laplace's Equations

AU : Dec.-03,09,14,18,19, May-06,07,11,12,14,18

• From the Gauss's law in the point form, Poisson's equation can be derived. Consider the Gauss's law in the point form as,

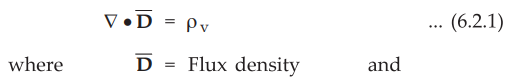
ρv = Volume charge density

• It is known that for a homogeneous, isotropic and linear medium, flux density and electric field intensity are directly proportional. Thus,

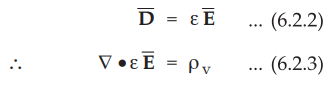
From the gradient relationship,

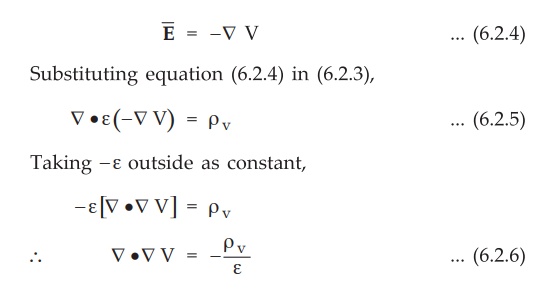
• Now 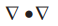 operation is called operation and denoted as .

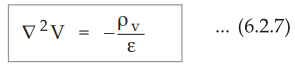
This equation (6.2.7) is called Poisson's equation.

• If in a certain region, volume charge density is zero (ρ v = 0), which is true for dielectric medium then the Poisson's equation takes the form,

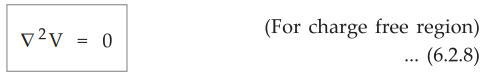
• This is special case of Poisson's equation and is called Laplace's equation. The  operation is called the Laplacian of V.

Key Point : Note that if p v =0, still in that region point charges, line charges and surface charges may exist at singular locations.

• The equation (6.2.7) is for homogeneous medium for which e is constant. But if e is not constant and the medium is in homogeneous, then equation (6.2.5) must be used as Poisson's equation for in homogeneous medium.

 

1.  Operation in Different Co-ordinate Systems

• The potential V can be expressed in any of the three co-ordinate systems as V (x, y, z), V (r, ϕ, z) or V (r, θ, ϕ). Depending upon it, the  operation required for Laplace's equation must be used.

• In cartesian co-ordinate system,

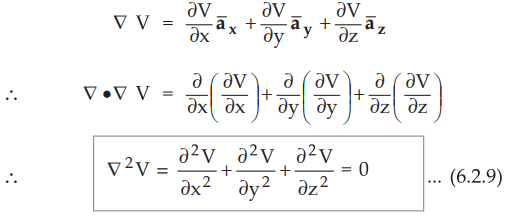
• The equation (6.2.9) is Laplace's equation in cartesian form.

• In cylindrical co-ordinate system,

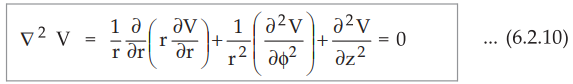
The equation (6.2.10) is Laplace's equation in cylindrical form.

In spherical co-ordinate system,

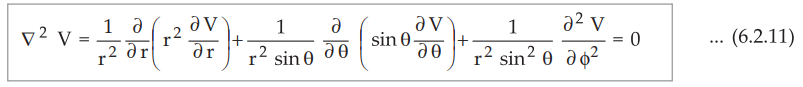
The equation (6.2.11) is Laplace's equation in spherical form.

 

Ex. 6.2.1 Determine whether or not the following potential fields satisfy the Laplace's equation : a)V = x² - y² + z² b) V = rcos ϕ+z c) V = rcos θ + ϕ

AU : May-11, Marks 8

Sol.: a) V = x² - y² + z²

 

Ex. 6.2.2 Given the potential field, V = 50 sin θ / r2 in free space, determine whether V satisfies Laplace's equation.

AU : May-07, Marks 8

Sol. :

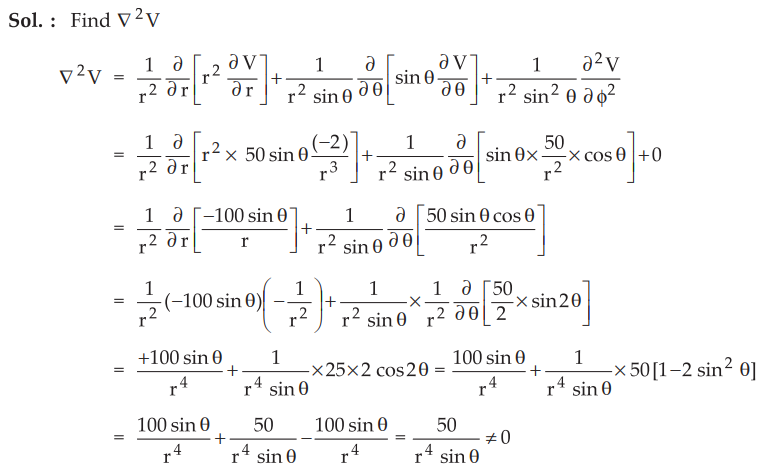
Hence given potential field does not satisfy Laplace's equation.

 

Ex. 6.2.3 Show that in cartesian coordinates for any vector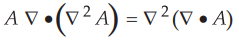 

AU : May-11, 12, Marks 8

Sol. : In cartesian system let the vector Ā is,

Ex. 6.2.4 If a potential :

V = x2yz + Ay3 z

Find ‘A’ s that Laplace’s equation is satisfied.

Sol. :

 

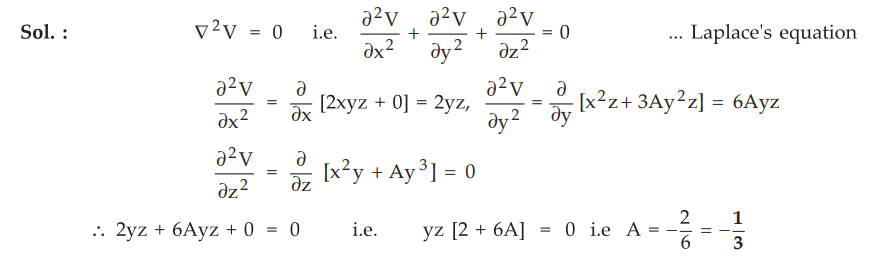
Ex. 6.2.5 Obtain an expression for the Laplacian operator in the cylindrical coordinates.

Sol. : In cartesian co-ordinates Laplacion operator is,

Using implicit differentiation of cos ϕ and sin ϕ expressions in equation (2),

This is Laplacian operator in cylindrical co-ordinates.

 

Examples for Practice

Ex. 6.2.6 Let V = 2xy²z³ and Ɛ = Ɛ₀. Given point is

P(l, 3, - 1). Find V at point P. Also find out if V satisfies Laplace's equation.

[Ans.: -18 V, does not satisfy]

Ex. 6.2.7 Let V₁ (r, θ, ϕ) = 6 / r and V₂ = (r, θ, ϕ) = 3

i) State whether V₁ and V₂ satisfy Laplace's equation.

ii) Evaluate V₁ and V₂ at r = 2.

[Ans.: i) Both V₁ and V₂ satisfy Laplace's equation, ii) 3]

Review Questions

1. Derive Laplace's and Poisson's equations front the Gauss's law.

AU : Dec.-03, 09, 14, 18, May-06, 18, Harks 8

2. Derive the Laplace's equation. Obtain the Laplacian's operator in the cylindrical coordinate

AU : May-14, Marks 16