Electromagnetic Theory: Unit V: Electromagnetic Waves
Polarization of Uniform Plane Waves
Linear, Elliptical, Circular | Electromagnetic Waves
• There are different types of polarization of a uniform plane wave as given below. 1) Linear polarization 2) Elliptical polarization 3) Circular polarization
Polarization of Uniform Plane Waves
•
The polarization of uniform plane waves is defined as time varying behaviour of
the electric field intensity vector ![]() at some fixed point in space,
along the direction of propagation.
at some fixed point in space,
along the direction of propagation.
•
Consider a uniform plane wave travelling in positive z-direction. Then the
field vectors ![]() and
and ![]() lie in x-y plane, which is perpendicular to the
direction of propagation of a uniform plane wave. Being an electromagnetic (EM)
wave, as wave travels in a space, both the fields undergo same variations with
respect to time.
lie in x-y plane, which is perpendicular to the
direction of propagation of a uniform plane wave. Being an electromagnetic (EM)
wave, as wave travels in a space, both the fields undergo same variations with
respect to time.
•
There are different types of polarization of a uniform plane wave as given
below.
1)
Linear polarization
2)
Elliptical polarization
3)
Circular polarization
•
In other words, the polarization is nothing but a way in which the magnitude
and direction of the electric field varies. These variations of the field are
observed in the direction of propagation of a wave. So if the variation of the
electric field ![]() is observed on a plane perpendicular to the direction
of propagation of wave, we get
is observed on a plane perpendicular to the direction
of propagation of wave, we get ![]() along straight line or circle or
ellipse.
along straight line or circle or
ellipse.
•
For the understanding of basic concept of polarization of a uniform plane wave,
let us assume that ![]() is the resultant of
is the resultant of  are directed along
x-direction and y-direction respectively. Also assume that the variations of
are directed along
x-direction and y-direction respectively. Also assume that the variations of  be sinusoidal similar to
be sinusoidal similar to ![]() . To get different types of the
polarization for
. To get different types of the
polarization for ![]() , consider different conditions for
, consider different conditions for  .
.
1. Linear Polarization
•
Consider that the electric field ![]() has only x-component and
y-component of
has only x-component and
y-component of ![]() is zero. Then looking from the direction of
propagation, the wave is said to be linearly polarized in x-direction.
Similarly if only the y-component in
is zero. Then looking from the direction of
propagation, the wave is said to be linearly polarized in x-direction.
Similarly if only the y-component in ![]() is present and
x-component of
is present and
x-component of ![]() is zero then the wave is said to be linearly
polarized in y-direction.
is zero then the wave is said to be linearly
polarized in y-direction.
•
Let us assume that both the components of ![]() are present denoted
by
are present denoted
by  . Both these components are in phase having different amplitudes.
As
. Both these components are in phase having different amplitudes.
As  are in phase they will have their amplitudes reaching
maximum or minimum value simultaneously. Also if the amplitude of
are in phase they will have their amplitudes reaching
maximum or minimum value simultaneously. Also if the amplitude of ![]() increases or decreases the amplitude of
increases or decreases the amplitude of ![]() also increases or
decreases. In other words, at any point along positive z-axis the ratio of
amplitudes of both the components is constant as both of them are in phase
having same wavelength.
also increases or
decreases. In other words, at any point along positive z-axis the ratio of
amplitudes of both the components is constant as both of them are in phase
having same wavelength.
•
The electric field![]() is the resultant of
is the resultant of  and the
direction of it depends on the relative magnitude of
and the
direction of it depends on the relative magnitude of  . Thus the
angle made by
. Thus the
angle made by ![]() with x-axis is given by,
with x-axis is given by,
θ
= tan-1 Ey / Ex
•
Where Ex and Ey are the magnitudes of  respectively.
respectively.
•
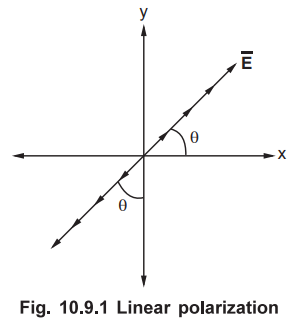
This angle is constant with respect to time. In other words, the resultant
vector ![]() is oriented in a direction which is constant with time, thus
the wave is said to be linearly polarized as shown in the Fig. 10.9.1.
is oriented in a direction which is constant with time, thus
the wave is said to be linearly polarized as shown in the Fig. 10.9.1.
•
When both the components have same amplitudes we get a polarization of ![]() as linear polarization with a constant angle of 45°.
as linear polarization with a constant angle of 45°.
•
From Fig. 10.9.1 it is clear that when Ex increases or decreases, Ey also
increases and decreases as both are in phase. And the resultant ![]() changes along the straight line at an angle θ° with respect to x-axis.
changes along the straight line at an angle θ° with respect to x-axis.
•
Thus when  components are in phase with either equal or unequal
amplitudes, for a uniform plane wave travelling in z-direction, the
polarization is linear.
components are in phase with either equal or unequal
amplitudes, for a uniform plane wave travelling in z-direction, the
polarization is linear.
2. Elliptical Polarization
•
Consider that the electric field ![]() has both the components which are
not having same amplitudes and are not in phase. As the wave propagates,
has both the components which are
not having same amplitudes and are not in phase. As the wave propagates,  will have maximum and minimum amplitudes at different instants
of time depending on the relative amplitudes of
will have maximum and minimum amplitudes at different instants
of time depending on the relative amplitudes of  at any instant of
time. In other words, the direction of the resultant field
at any instant of
time. In other words, the direction of the resultant field ![]() varies
with time. If the locus of the end points of
varies
with time. If the locus of the end points of ![]() is traced, it is
observed that
is traced, it is
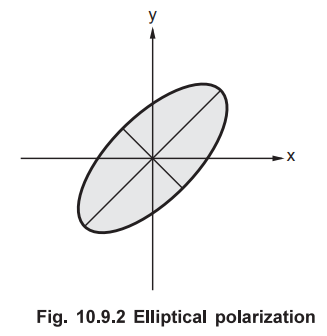
observed that ![]() moves elliptically. Then such a wave is said to be elliptically
polarized as shown in the Fig. 10.9.2.
moves elliptically. Then such a wave is said to be elliptically
polarized as shown in the Fig. 10.9.2.
•
When the amplitudes of  are different and the phase difference
between the two is other than 90°, then the axes of the ellipse are inclined at
an angle 0 with the co-ordinate axes.
are different and the phase difference
between the two is other than 90°, then the axes of the ellipse are inclined at
an angle 0 with the co-ordinate axes.
•
When this phase difference between  is exactly 90°, then the axes of
the ellipse lie along the co-ordinate axes.
is exactly 90°, then the axes of
the ellipse lie along the co-ordinate axes.
•
Let us consider that the amplitudes of  components are unequal. Let
the phase difference between the two components be 90° exactly. The maximum
amplitude of
components are unequal. Let
the phase difference between the two components be 90° exactly. The maximum
amplitude of  will occur at different instants of time. Thus the
direction of
will occur at different instants of time. Thus the
direction of ![]() varies with time, along an ellipse as shown in the
Fig. 10.9.3. Refer Fig. 10.9.3
varies with time, along an ellipse as shown in the
Fig. 10.9.3. Refer Fig. 10.9.3
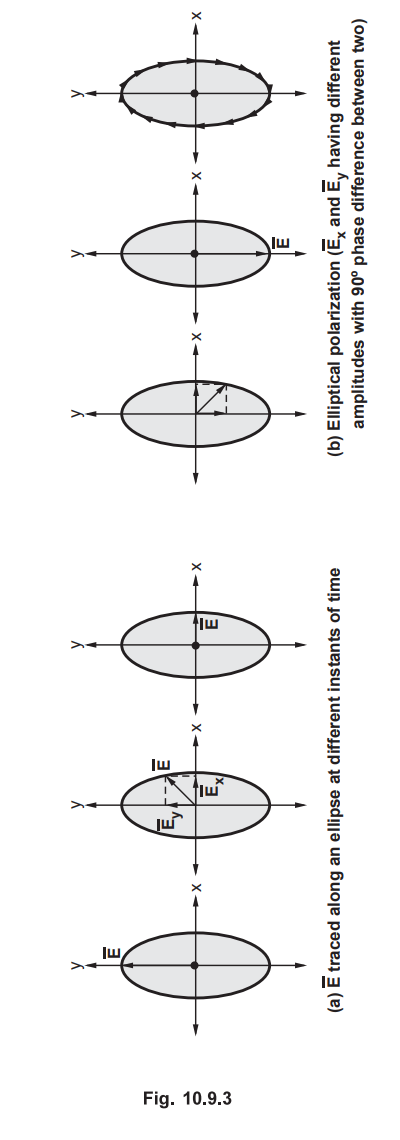
With
90° phase difference between  ;
;
i)
The major axis of an ellipse lies along y-axis if the amplitude of ![]() is greater than that of the component
is greater than that of the component ![]() and
and
ii)
The major axis of an ellipse lies along x-axis, if the amplitude of![]() is greater than that of
is greater than that of ![]()
•
Thus when the components  of unequal amplitudes have a
constant, non-zero phase difference between two, for a uniform plane wave
z-direction, the polarization is travelling in elliptical.
of unequal amplitudes have a
constant, non-zero phase difference between two, for a uniform plane wave
z-direction, the polarization is travelling in elliptical.
3. Circlar Polarization
•
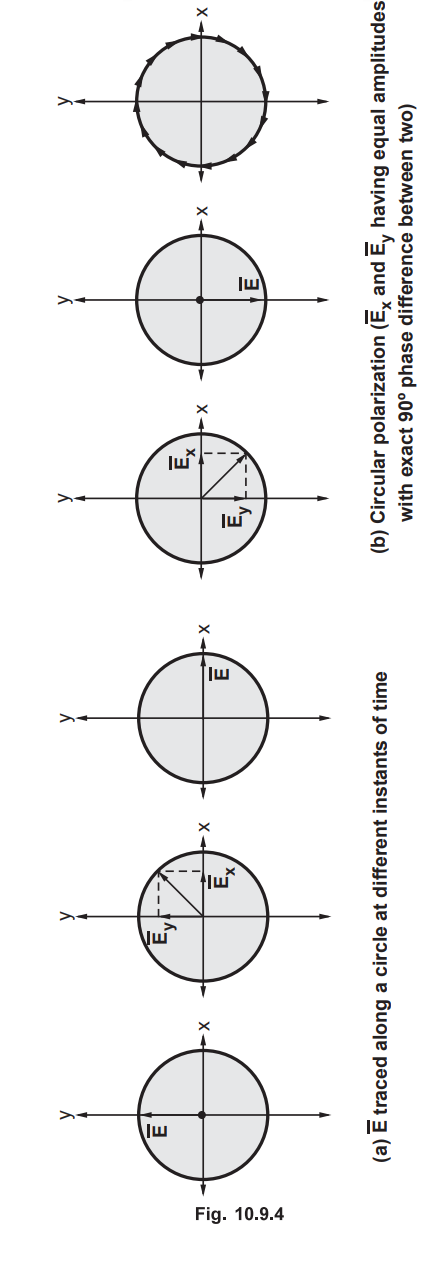
Let us consider that ![]() has two components,
has two components,  , of equal
amplitude but the phase difference between them is exactly 90°. At any instant
of time, when the amplitude of any one of the component is maximum, then the
amplitude of the remaining component becomes zero. Also when any component
gradually increases or decreases; the other component gradually decreases or
increases respectively. Thus at any instant of time the magnitude of the
resultant vector
, of equal
amplitude but the phase difference between them is exactly 90°. At any instant
of time, when the amplitude of any one of the component is maximum, then the
amplitude of the remaining component becomes zero. Also when any component
gradually increases or decreases; the other component gradually decreases or
increases respectively. Thus at any instant of time the magnitude of the
resultant vector ![]() is constant. But the direction of the resultant
vector
is constant. But the direction of the resultant
vector ![]() changes with respect to the time as the angle depends on
the relative amplitudes of the two components at every instant. If
changes with respect to the time as the angle depends on
the relative amplitudes of the two components at every instant. If ![]() is projected on a plane perpendicular to the direction of propagation, then the
locus of all such points is a circle with the centre on z-axis. In one wavelength
span, the resultant vector
is projected on a plane perpendicular to the direction of propagation, then the
locus of all such points is a circle with the centre on z-axis. In one wavelength
span, the resultant vector ![]() completes one cycle of rotation. Then
such a wave is said to be circularly polarized as shown in the Fig. 10.9.4
Refer Fig. 10.9.4.
completes one cycle of rotation. Then
such a wave is said to be circularly polarized as shown in the Fig. 10.9.4
Refer Fig. 10.9.4.
•
If ![]() is having components in both x and y-directions, we can write,
is having components in both x and y-directions, we can write,
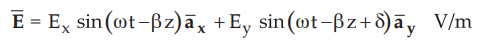
•
Where δ is the phase shift between two components.
Consider
that field ![]() is observed at z = 0. Then
is observed at z = 0. Then
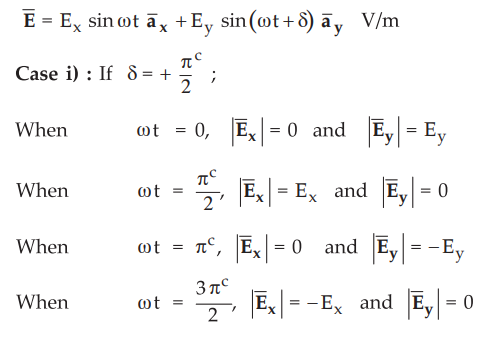
•
Graphically it is represented as shown in the Fig. 10.9.5.
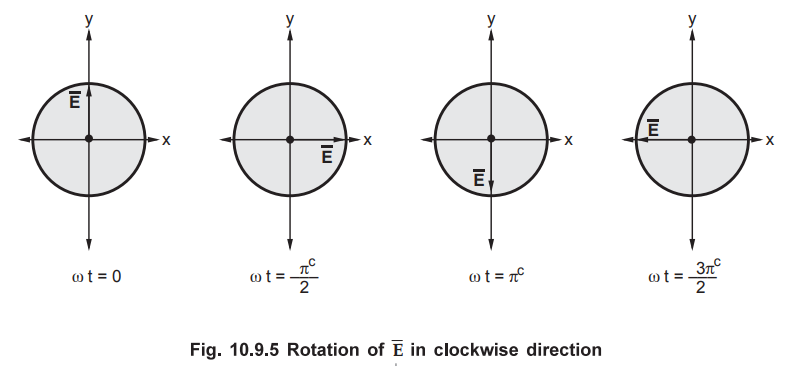
•
From the Fig. 10.9.5 it is clear that the resultant vector ![]() rotates
in clockwise direction, such that the locus of all such points represents a
circle. As per IEEE definitions, this type of polarization is called left
circular polarization.
rotates
in clockwise direction, such that the locus of all such points represents a
circle. As per IEEE definitions, this type of polarization is called left
circular polarization.

Graphically
resultant ![]() can be represented as shown in the Fig. 10.9.6.
can be represented as shown in the Fig. 10.9.6.
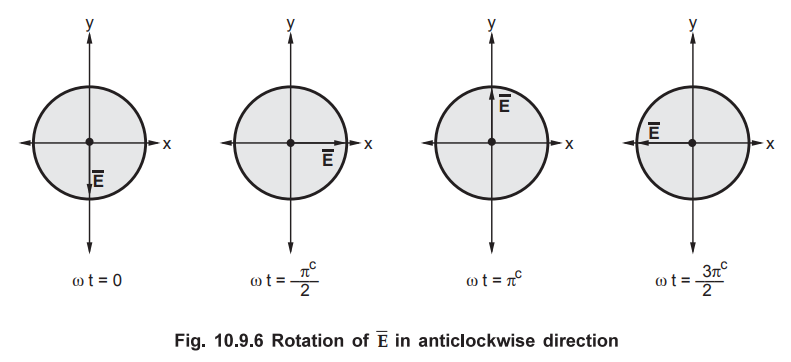
•
From the Fig. 10.9.6 it is clear that the resultant vector ![]() rotates
in anticlockwise direction, such that the locus of all such points represents a
circle. As per IEEE definitions, this type of polarization is called right
circular polarization.
rotates
in anticlockwise direction, such that the locus of all such points represents a
circle. As per IEEE definitions, this type of polarization is called right
circular polarization.
•
Any electric wave has two components ;
i)
Forward travelling component Em sin (ωt - βz)
ii)
Backward travelling component Em sin (ωt + β z)
•
Note that the definitions of right and left circular polarization are obtained
for the forward travelling wave. For backward travelling wave the definitions
of right and left circular polarization are exactly opposite to the previous
one.
•
Thus when two components  of equal amplitudes have a constant,
non-zero phase difference of 90° between them, for a uniform plane wave, the
polarization is circular.
of equal amplitudes have a constant,
non-zero phase difference of 90° between them, for a uniform plane wave, the
polarization is circular.
4. Conditions for the Polarization of a Sinusoidal Wave
•
Consider that the electric field ![]() of a uniform plane wave travelling
in z-direction is expressed as
of a uniform plane wave travelling
in z-direction is expressed as

•
This can be expressed in the time varying form as

•
As the wave propagates in z-direction, ![]() must lie in a plane
perpendicular to the direction of propagation i.e. x-y plane. Thus
must lie in a plane
perpendicular to the direction of propagation i.e. x-y plane. Thus ![]() is a resultant of two components
is a resultant of two components  along x-axis and y-axis
respectively. Let E1 and E2 be the amplitudes of
along x-axis and y-axis
respectively. Let E1 and E2 be the amplitudes of  respectively. Assume that both the variations are sinusoidal. Let δ be the
phase difference between the two components.
respectively. Assume that both the variations are sinusoidal. Let δ be the
phase difference between the two components.
•
The two components can be expressed in phasor form as,

•
As the electric field vector E is the resultant of Ex and Ey, we can write,

•
Equation (10.9.5) is true for all values of z. At z = 0, the equation (10.9.5)
can be rewritten as,
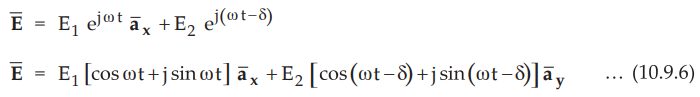
•
In general, the electric field vector can be represented with its two
components as,
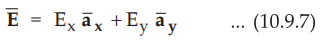
•
Equating right hand side of equation (10.9.7) with the real part of the
equation (10.9.6),

•
Above equation is the equation for polarization of sinusoidal wave. By applying
different conditions to equation for the polarization of sinusoidal wave, we
get different types of the polarization.
Condition
1 :  components are in phase i.e. δ = 0.
components are in phase i.e. δ = 0.
•
Substituting this condition in equation (10.9.14) we can write,

•
For a given wave, the amplitudes of  remain constant i.e.
Ei and E2 are constant. Thus the ratio (E1 / E2) is also
constant. Then the equation (10.9.15) is similar to the equation of a straight
line passing through origin, i.e. y = mx. Then the wave is said to be linearly
polarized wave.
remain constant i.e.
Ei and E2 are constant. Thus the ratio (E1 / E2) is also
constant. Then the equation (10.9.15) is similar to the equation of a straight
line passing through origin, i.e. y = mx. Then the wave is said to be linearly
polarized wave.
Condition
2 :  components of unequal amplitudes with a phase difference δ ≠ 0.
Let us assume that δ = π/ 2c.
components of unequal amplitudes with a phase difference δ ≠ 0.
Let us assume that δ = π/ 2c.
•
Applying conditions to equation (10.9.14), we can write,
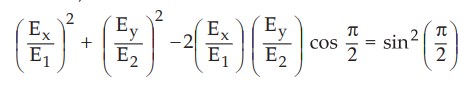
We
know that,
sin2
θ = 1/2 (l - cos2 θ), hence
we get sin21 (π/ 2) = 1
•
Then equation becomes
(Ex
/ E1)2 + (Ey / E2)2 = 1 ... (10.9.16)
•
Equation (10.9.16) represents equations for an ellipse. Thus, the wave, with
the components specified in the condition, is said to be elliptically
polarized.
Condition
3 :  components of equal amplitude with the phase difference between two as
components of equal amplitude with the phase difference between two as
δ
= πc / 2
•
Let the amplitude of  be equal to E0.
be equal to E0.
•
Applying conditions to equation (10.9.14), we can write,
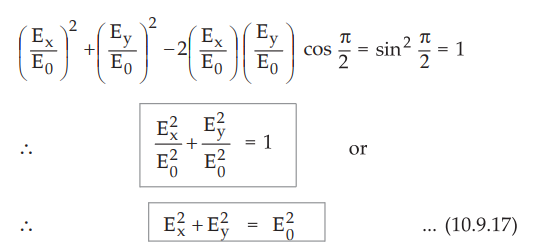
•
Equation (10.9.17) represents equation of a circle similar to x2 + y2
= a2. Thus the wave, with the components specified in the condition
is said to be circularly polarized.
Ex.
10.9.1 The electric field of a uniform plane wave is given by
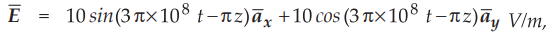
find
the polarization of the wave.
Sol.
:
The electric field of an uniform plane wave is given by,
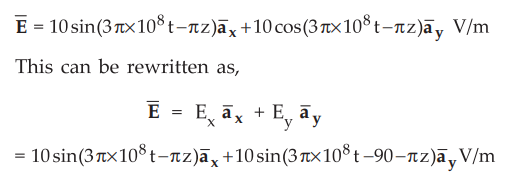
•
From above equation it is clear that the magnitudes of x and y components of ![]() are equal. (Ex = Ey = 10). At the same time the phase
difference between these two components is 90s. Hence the wave is circularly polarized.
are equal. (Ex = Ey = 10). At the same time the phase
difference between these two components is 90s. Hence the wave is circularly polarized.
Review Questions
1. What is polarization of uniform plane waves ? Write notes on
i) Linear polarization,
ii) Elliptical polarization
iii) Circular polarization.
2. Derive the condition for polarization of a sinusoidal wave.
Electromagnetic Theory: Unit V: Electromagnetic Waves : Tag: : Linear, Elliptical, Circular | Electromagnetic Waves - Polarization of Uniform Plane Waves
Related Topics
Related Subjects
Electromagnetic Theory
EE3301 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
