Potential Difference due to Infinite Line Charge

Potential Difference due to Infinite Line Charge

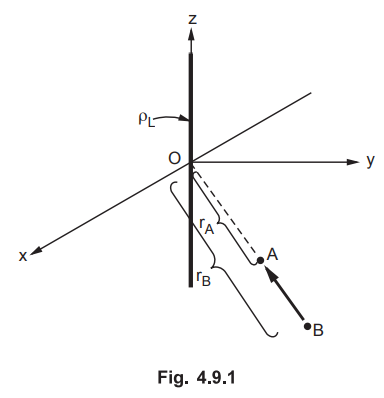
• Consider an infinite line charge along z-axis having uniform line charge density ρ L C/m

• The point B is at a radial distance rB while point A is at a radial distance r_A from the charge, as shown in the Fig. 4.9.1.

• The  due to infinite line charge along z-axis is known and given by,

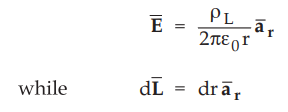
in cylindrical system in radial direction.

Important note : This is a standard result and may be used to find potential difference between the points due to infinite line charge. Remember that rA and rB are radial distances in cylinderical co-ordinate system i.e. perpendicular distances from charge, thus do not forget to find perpendicular distances rA Mid rB while using this result. The result can be used for any zero reference as potential difference calculation does not depend on the reference.

Ex. 4.9.1 Calculate potential difference V_AB for a line charge ρL = 5 nC/m on the z-axis where A(2m,π/2, 0) and B(4m,π,5m).

Sol. : The charge is shown in the Fig. 4.9.2.

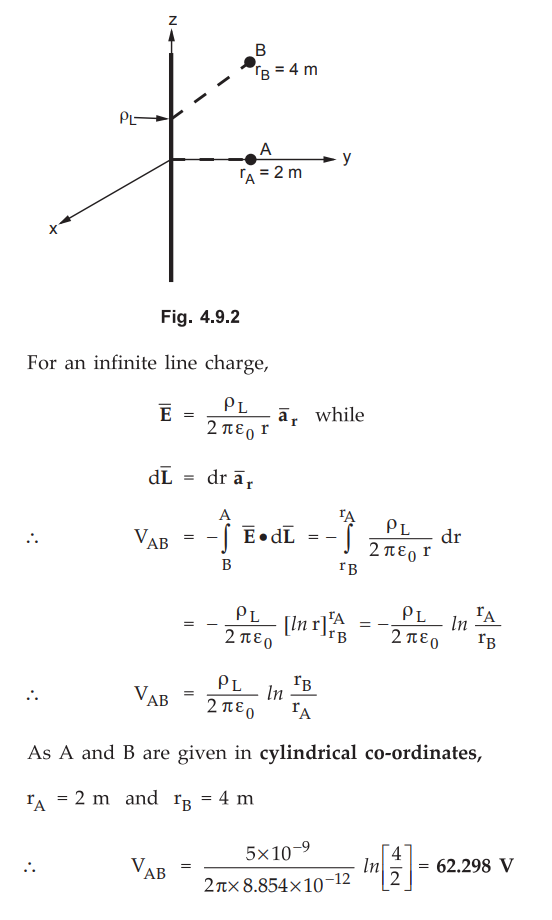
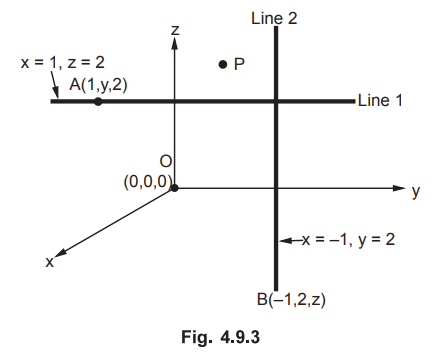
Ex. 4.9.2 Two uniform line charges, 8 nChn are located at x = 1, z = 2 and at x = - 2, y = 2 in free space. If the potential at origin is 100 V, find V at P (4, 1, 3).

Sol. : The two line charges are shown in the Fig. 4.9.3.

Now V = 100 V at the origin O (0, 0, 0).

Let us obtain potential difference V_PO using standard result.

Case 1 : Line charge 1

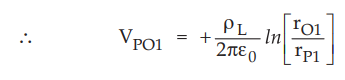
where r_O1 and r_P1 are perpendicular distances of points O and P from the line 1. The line 1 is parallel to y-axis so do not use y co-ordinates to find r_O1 and r_p1.

Case 2 : Line charge 2, which is parallel to z-axis.

Do not consider z co-ordinate to find perpendicular distance.

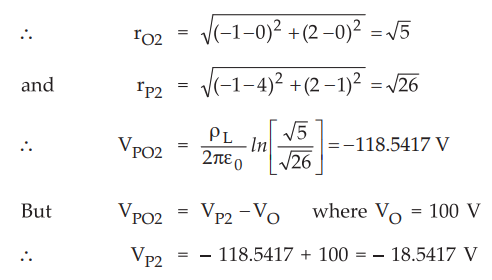
This is absolute potential of P due to line charge 2

V_P = V_P1 + V_P2 = 50.16 - 18.5417

= 31.6183 V

Note : Students can use the method of using consant C to find absolute potential of P due to line charge 1 and line charge 2. Adding the two, potential of P can be obtained. The answer remains same. For reference, the constant C₁ = C₂ = 215.721 for both the line charges.

Examples for Practice

Ex. 4.9.3 Two cylindrical tubes each having an outer radius of 15 cm are located in air, parallel and external to each other, with a centre to centre spacing of 0.9 m. The electric potential difference between them is 2500 V. How far from the surface of the conductor of lower potential measured along the line joining their centres is the electric poential 750 V above that of the conductor of lower potential ?

[Ans.: 0.2567 m]

Ex. 4.9.4 A uniform sheet of charge ρS1 = 50 Ɛ0 C/m² is located at z =     1.5 m while ρS2 = -50 Ɛ0 C/m² is at z = - 0.5 m.

a) Find  everywhere

b) Find and sketch V (z) as a function of z for - 0.5 < z < 1.5 if V = 0 at z = - 0.5 m.

Ex, 4,9.5 Giuen a point charge of 200 ne0 C at C(3,-l,+ 2), a line charge of 40KE0 C/m on the x-axis and a surface charge of 8 £gC/mz on the plane x = -3, all in the free space. Find the potential at P (5, 6, 7) if V = 0 V at Q (0, 0, 1).   

[Ans.: - 73.8406 V]

Review Question

1. Derive the expression for the potential difference due to infinite line charge.