Electromagnetic Theory: Unit II: (a) Electric Work Potential and Energy
Potential due to a Line Charge
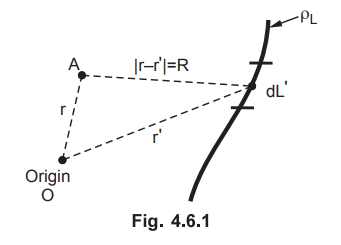
• Consider a line charge having density ρL C/m, as shown in the Fig. 4.6.1.
Potential due to a Line Charge
AU
: May-05, 09
•
Consider a line charge having density ρL C/m, as shown in the Fig. 4.6.1.
•
Consider differential length dL' at a distance r'. Then the differential charge
on the length dL' is given by,
dQ
= ρL(r ')dL' ...(4.6.1)
where ρL(r') = Line charge density at r'
Let the potential at A is to be determined. Then
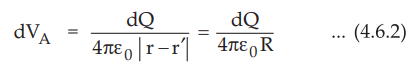
•
The R = |r - r '| indicates the distance from the differential charge.
•
The dVA is a differential potential at A. Hence the potential VA
can be obtained by integrating dVA over the length over which
line charge is distributed.

Key
Point : Note that R is the distance and not the vector and
for uniform line charge density ρL(r') = ρL.
Ex.
4.6.1 Find the potential V on z-axis at a distance z from origin when uniform
line charge ρL in the form of a ring of radius a is placed in the z = 0 plane.
Sol.
:
The arrangement is shown in the Fig. 4.6.2.
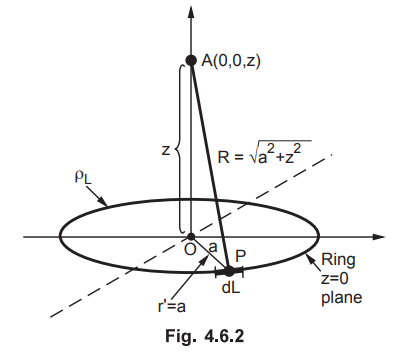
The
point A (0, 0, z) is on z-axis, at a distance z from the origin while radius of
the ring is a.
Consider
differential length dL' at point P on the ring. The ring is in z = 0 plane
hence dL' in cylindrical system is,
dL
= r’d ϕ
= ad ϕ
The
distance of point A from the differential charge is R = l (PA).
R
= √a2 + z2 ... From
the Fig. 4.6.2
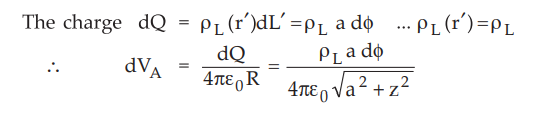
Hence
the potential of A is to be obtained by integrating dVA over the circular ring
i.e. path with radius r' = a and 0 varies from 0 to 2 π
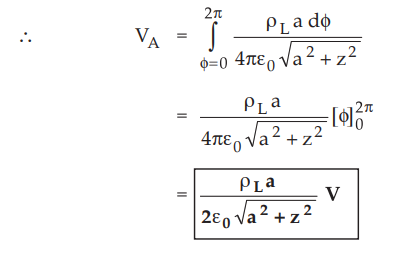
Important
Key
Point : Note that the potential at a point can be obtained
by two ways.
1.
If ![]() is known then use,
is known then use,
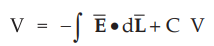
C
= 0 if reference is infinity.
2.
If ![]() is not known, then find differential charge dQ considering
differential length dL' and
is not known, then find differential charge dQ considering
differential length dL' and
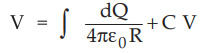
The
integration depends on the charge distribution.
Ex.
4.6.2 A uniform line charge of 1 nCIm is situated along x-axis between the
points (-500, 0) and (500, 0) mm. Find the electric scalar potential at
(0,1000) mm.
AU
: May-05, Marks 10
Sol
. :
ρL
= 1 nC/m along x-axis and find V at A (0, 1000) mm.
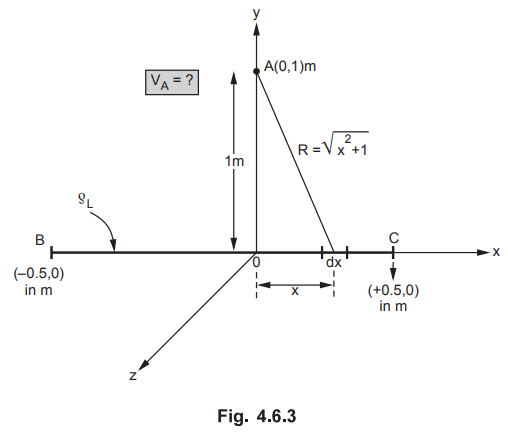
Sol
. :
Consider
elementary charge dQ on length dx at distance x from orign.
dQ
= ρL dx
Distance
of point A from charg dQ is
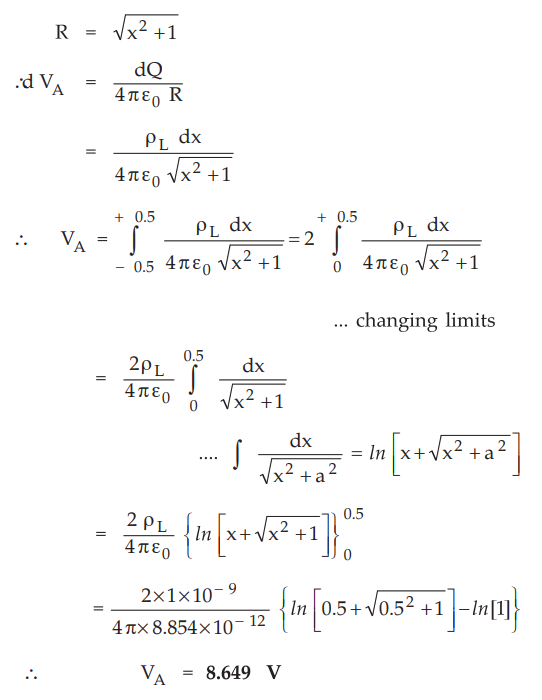
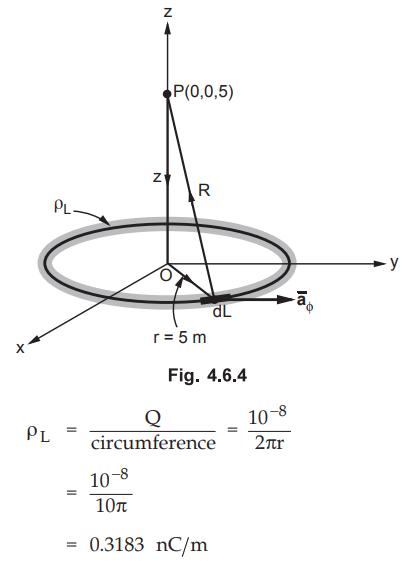
Ex. 4.6.3 A total charge of 10 -8 C is distributed uniformly along a ring of radius of 5 m. Calculate the potential on the axis of the ring at a point 5 m from the centre of the ring.
Sol.
:
Q = 10-8 C, r = 5 m, h = 5 m. The ring is shown in the Fig. 4.6.4.
Consider
the differential length dL on the ring.
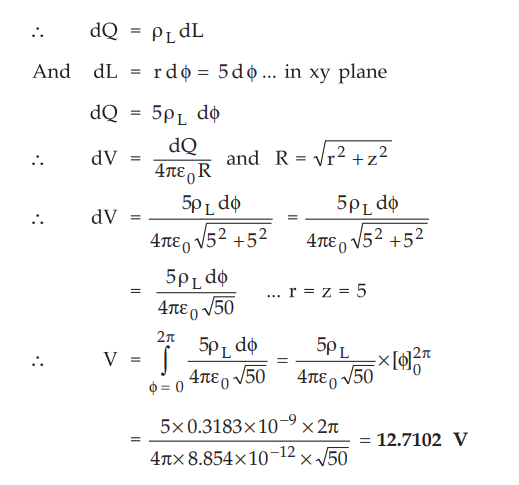
Example
for Practice
Ex.
4.6.4 A uniform line charge density pL C/m is
existing from - L to + L on y-axis. Find potential at A (a, 0, 0).
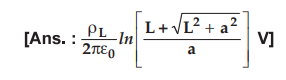
Ex.
4.6.5 A total charge of 40/3 nC is uniformly
distributed over a circular ring of radius 2 m placed in z = 0 plane, with
center as origin. Find the electric potential at A (0, 0, 5).
[Ans.:
22.252 V]
Electromagnetic Theory: Unit II: (a) Electric Work Potential and Energy : Tag: : - Potential due to a Line Charge
Related Topics
Related Subjects
Electromagnetic Theory
EE3301 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
