Potential due to Point Charge

Potential due to Point Charge

AU : May-04, 05, 10, 11, 16, 18, Dec.-02, 04, 14, 16,18

• Consider a point charge, located at the origin of a spherical co-ordinate system, producing   radially in all the directions as shown in the Fig. 4.5.1.

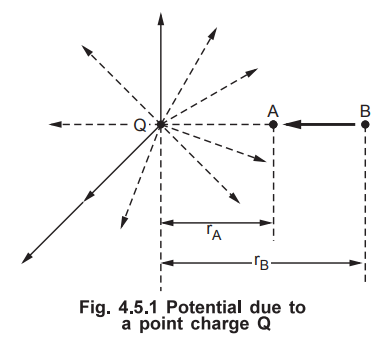
• Assuming free space, the field    due to a point charge Q at a point having radial distance r from origin is given by,

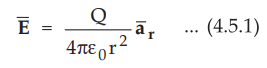
• Consider a unit charge which is placed at a point B which is at a radial distance of rB from the origin. It is moved against the direction of    from point B to point A. The point A is at a radial distance of rA from the origin.

• The differential length in spherical system is,

• Hence the potential difference VAB between points A and B is given by,

• when rB > rA, 1 / rB < 1 / rA and VAB positive. This indicates the work is done by external source in moving unit charge from B to A.

1. Concept of Absolute Potential

AU : May-10

• Instead of potential difference, it is more convenient to express absolute potentials of various points in the field. Such absolute potentials are measured with respect to a specified reference position. Such a reference position is assumed to be at zero potential.

• For practical circuits, zero reference point is selected as 'ground'. All the potentials of the circuit are measured with respect to ground which is treated to be zero potential reference. The example of such a reference is a shielded cable. The conductor is shielded as shown in the Fig. 4.5.2. The outer shield is grounded to minimise the interference of the external signals with the signal carried by inner conductor. In such a case outer shield is taken as a reference with respect to which, potentials of various points are defined.

• Similalrly in cathode ray tube, the metallic shield around the tube is taken as zero potential reference. With respect to this reference, potentials of various points are measured.

Key Point: Most widely used reference which is used to develope the concept of absolute potential is infinity. The potential at infinity is treated to be zero and all the potentials at various points in the field are defined with reference to infinity.

• Consider potential difference VAB ^ue to movement of unit charge from B to A in a field of a point charge Q. It is given by equation (4.5.3).

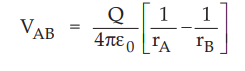
• Now let the charge is moved from infinity to the point A i.e. rB = ∞

Hence 1 / rB = 1/ ∞ = 0.

• The quantity represented by equation (4.5.4) is called potential of point A denoted as VA .

VA = Q / 4πƐ0rA … (4.5.5)

• This is also called absolute potential of point A.

• Similarly absolute potential of point B can be defined as,

VB = (Q / 4πƐ0r ) V … (4.5.6)

• This is work done in moving unit charge from infinity at point B.

• Hence the potential difference can be expressed as the difference between the absolute potentials of the two points.

VAB = (VA – VB) V ….. (4.5.7)

• Thus absolute potential can be defined as,

Key Point : The absolute potential at any point in an electric field is defined as the work done in moving a unit test charge from the infinity (or reference point at which potential is zero) to the point, against the direction of the field.

• Hence absolute potential at any point which is at a distance r from the origin of a spherical system, where point charge Q is located, is given by,

V = Q / 4πƐ0r

• The reference point is at infinity.

Key point : Note that the potential is a scalar quantity.

• Other way to define potential mathematically is,

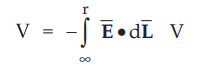
(where ∞ is selected as the reference.)

Thus, 

• This is potential of point A with reference at infinity.

2. Potential due to Point Charge Not at Origin

• If the point charge Q is not located at the origin of a spherical system then obtain the position vector r' of the point where Q is located.

• Then the absolute potential at a point A located at a distance r from the origin is given by,

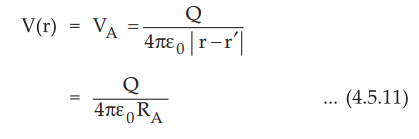
where RA =| r - r'| = Distance between point at which potential is to be calculated and the location of the charge

Key Point : R is only the distance and not the vector. The potential is a scalar quantity hence only distance R =| r - r '| is involved in the determination of potential of point A. The reference is still infinity.

3. Potential due to Several Point Charges

AU : May-04

• Consider the various point charges Q 1, Q2 ... Qn located at the distances r1 r2 ... rn from the origin as shown in the Fig. 4.5.4. The potential due to all these point charges, at point A is to be determined. Use superposition principle.

• Consider the point charge Q1

• The potential VA1 due to Q1 is given by,

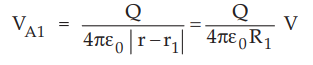
where R1 =| r – r1| = Distance between point A and position of Q1

The potential VA2 due to Q2 is given by,

Thus potential VAn due to Qn is given by,

• As the potential is scalar, the net potential at point A is the algebraic sum of the potentials at A due to individual point charges, considered one at a time.

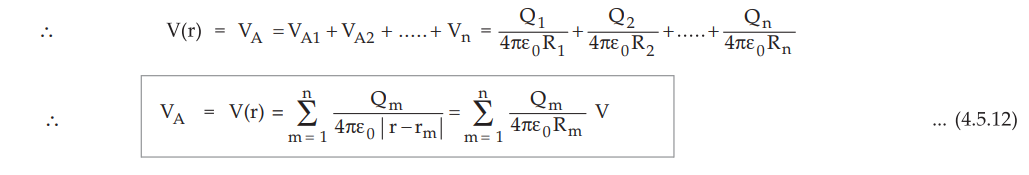
Key Point : Note that the reference point of zero potential is still assumed to be at infinity.

Ex. 4.5.1 Two point charges -4pC and 5,nC are located at (2, - 1, 3) and (0, 4,- 2 ) respectively. Find the potential at (1, 0, 1) assuming zero potential at infinity.

Sol. : The charges are shown in the Fig. 4.5.5.

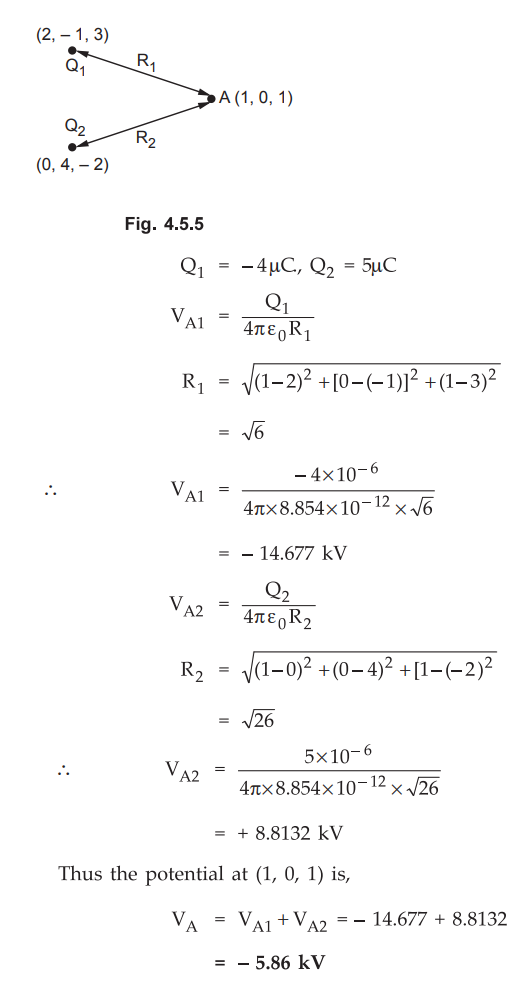
4. Potential Calculation When Reference is Other Than Infinity

• The expressions derived uptill now are under the assumption that the reference position of zero potential is at infinity.

• If any other point than infinity is selected as the reference then the potential at a point A due to point charge Q at the origin becomes,

VA = (Q / 4πƐ0RA) + C

where          C = Constant to be determined at

choosen reference point where V = 0.

• Note that the potential difference between the two points is not the function of C.

Key Point : Another important note is that if the potential difference is to be calculated then reference is not needed. The reference is important only when the absolute potential is to be calculated.

• The idea will be clear from the following examples.

Ex. 4.5.2 A point charge of 6 nC is located at origin in free space, find potential of point P if P is located at (0.2, - 0.4, 0.4) and a) V = 0 at infinity b) V = 0 at (1, 0, 0) c)V = 20 Vat (- 0.5, 1, - 1).

Sol. : a) The reference is at infinity, hence

b) V = 0 at (1, 0, 0). Thus the reference is not at infinity. In such a case potential at P is,

This is with reference to (1, 0, 0) where V = 0 V.

c) Now V = 20 V at (- 0.5, 1, -1). Let this point is M (- 0.5, 1, - 1). The reference is not given as infinity.

Key Point : Note that distance of P from origin where Q is located is Rp which is same in all the cases. Only 'C' changes as the reference changes hence VP changes.

Ex. 4.5.3 VVTwf is the potential at the center of a square with a side a = 2 m while charges 2 µC, -4µ C, 6µ C and 2µ C are located at its four corners ?

Sol. : The arrangement of charges is shown in the Fig. 4.5.9.

The potential at a point due to a point charge is given by,

Ex. 4.5.4 Given a field

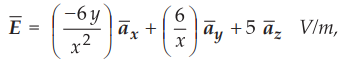Find the potential difference VAB given A(-7,2,l) and B(4,l,2).

AU : Dec.-02, May-11, Marks 8

Sol. :

To obtain the integral as it does not depend on the path from B (4, 1, 2) to A (- 7,2,1) we can divide the path as,

Alternatively find the equations for straight line path from B to A by using,

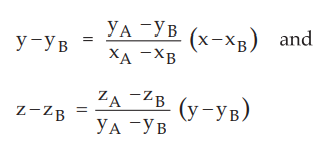
and using the relations between x, y and z solve the integrals. From the above equations we get, x = - 11 y + 15 and z = - y + 3 so use y interms of x for first integral and x interms of y for the second integral and integrate.

Ex. 4.5.5 find the potential at rA = 5 m with respect to rB = 15 m due to point charge Q = 500 pC at the origin and zero reference at infinity.

AU : Dec.-16, Marks 6

Sol. : As zero reference is at infinity and Q = 500 pC at origin, the potential due to point charge is,

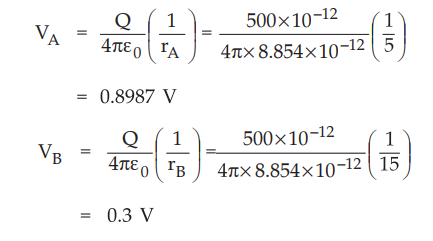
Potential at A with respect to B = VAB = VA - VB

= 0.8987 - 0.3 = 0.5987 V

Ex. 4.5.6 Two point charges - 4 µC and 5 ,µC are located at (2, -1, 3) and (0, 4, -2) respectively. Find the potential at (1, 0, 1) assuming zero potential at infinity.

AU : Dec.-14, Marks 6

Sol. : Refer Example 4.5.1 for the procedure and verify the answer as :

Ex. 4.5.7 Calculate the potential at a point P(0, 0) m due to point charges Q1 and Q2. Q1 = 10-12 Coulomb is located at (0.5, 0) m and Q2 = -10-11 Coulomb is located at (- 0.5, 0) m.

AU ; May-16, Marks 6

Sol. :

Examples for Practice

Ex. 4.5.7 A point charge Q = 0.4 nC is located at the origin. Obtain the absolute potential of A (2, 2, 3).     

[Ans. :0.8719 V]

Ex. 4.5.8 If same charge Q = 0.4 nC in above example is located at (2, 3, 3) then obtain the absolute potential of point A (2, 2, 3).

[Ans.: 3.595 V]

Ex. 4.5.9 If the point B is at (- 2, 3, 3) in the above example, obtain the potential difference between the points A and B.

[Ans.: 2.6962 V]

Ex. 4.5.10 Two charges of opposite sign and magnitude 1 pC are located 1 m apart. Find the potential at a point located midway between the two charges and 50 cm from the line connecting the charges. What shall be potential if the charges have similar sign ?

[Ans.: 0 V, 0.03595 V, 0.01797 V]

Ex. 4.5.11 The potential difference between two concentric sphere of radii r1 and r2 (r2 > r1) is V. Show that the electric field at the surface of the inner sphere is minimum of 2V/r1 for r1 = r2/2.

Ex. 4.5.12 A point charge of 5 nC is located at the origin. If V = 2 V at (0, 6, - 8) Find :

i) The potential at A (- 3, 2, 6)

ii) The potential at B (1, 5, 7)

iii) Potential difference VAB

[Ans.: i) 3.926 V, ii) 2.6952 V, iii) + 1.23 V]

Ex. 4.5.13 Find the potential at rA = 5 m and r B = 15 m due to point charge Q = 500 pC placed at the origin. Find the potential at rA = 5 m assuming zero as potential at infinity. Also obtain the potential difference between points A and B.

[Ans.: 0.5987 V, 0.599 V]

Ex. 4.5.14 A 15 nC point charge is at the origin in free space. Calculate if point P is located at (2, -3, -1). Also calculate 1/j at P if V = 0 at (6, 5, 4).

[Ans.: i) 36.0311 V, ii) 20.6673 V]

Review Questions

1. Obtain the expression for the potential due to point charge.

2. Distinguish potential and potential difference.

3. Define potential.