Potential due to Surface Charge

Potential due to Surface Charge

AU : May-08, 13

Consider uniform surface charge density ρs C/m² on a surface, as shown in the Fig. 4.7.1.

• Consider the differential surface area dS' at point P where p s is indicated as ρ s(r')

• The differential charge can be expressed as,

where R = Distance of point A from the differential charge

• The total potential at A can be obtained by integrating dV_A over the given surface.

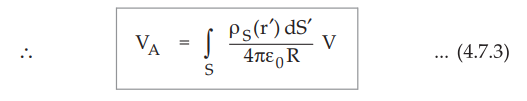
• Note that for uniform surface charge density ρ S (r') = ρS.

Ex. 4.7.1 Find the potential due to charged circular disc having uniform surface charge density of ρS c/m² at a height 'h' an its axis.

Sol. : Let the disc of radius 'a' is placed in x-y plane and z is its axis. The disc is charged with uniform charge density of ρS as shown in the Fig. 4.7.2.

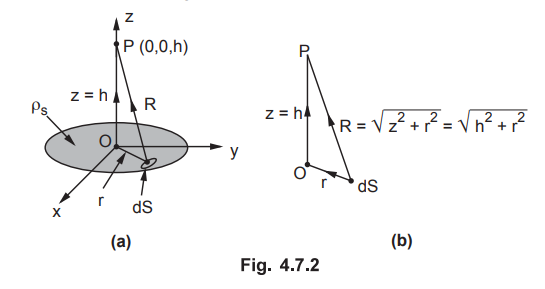
Consider the differential surface area dS with a charge dQ = ρS dS. As dStis in the x-y planeti.e. normal direction is 

The potential due to charged disc at point P is given by,

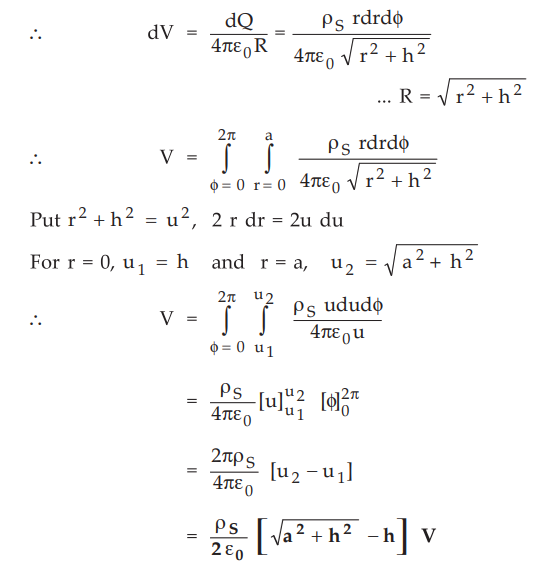
This is the required potential due to charged disc of radius 'a', at a height 'h' along its axis.

Examples for Practice

Ex. 4.7.2 Two concentric cylindrical conductors are arranged to form a coaxial transmission line. Prove that the potential difference between the conductors is given by,

where a = Radius of inner cylinder, b = Radius of outer cylinder, p£ = Charge per unit length of the inner conductor.

Ex. 4.7.3 A total charge of 1CF8 C is distributed uniformly along a ring of radius 5 m. Calculate the potential on the axis of the ring at a point 5 m from the centre of the ring. If the same charge is uniformly distributed on a disc of 5 m radius, what will be the potential on its axis at 5 m from the centre ?

[Ans.: 12.7101 V, 14.8909 V]

Ex. 4.7.4 Show that the potential at the origin due to the uniform surface charge density ρS over a ring z = 0 and radius between R < r < R +1, is independent of R.

[Ans. : ρS / 2Ɛ₀ V]

Ex. 4.7.5 A total charge of 40/3 nC is uniformly distributed over a circular disc of radius 2 m. Find the potential at a point on the axis 5 m from the plane of the disc.

[Ans.: 23.0776 V]

Review Question

1. Explain potential due to charged disc.