Potential due to Volume Charge

Potential due to Volume Charge

• Consider a uniform volume charge density p v C/m³ over the given volume as shown in the Fig. 4.8.1.

• Consider the differential volume dv' at point P where the charge density is ρv (r').

• The differential charge can be expressed

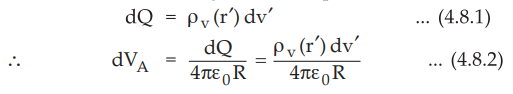
where R = Distance of point A from the differential charge

• The total potential at A can be obtained by integrating dVA over the given volume.

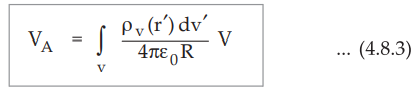
• Note that for uniform volume charge density ρv(r') = ρV

Ex. 4.8.1 Find the potential of a uniformly charged spherical shell of radius R at points inside and outside.

Now total charge contained by sphere is,

4-E or

AU : May-03, Marks 8

Sol. : Consider a sphere of radius R with a uniform charge density ρv.

Case 1 : Let point P is outside sphere (r > R).

The   is directed radially outwards, along   direction.

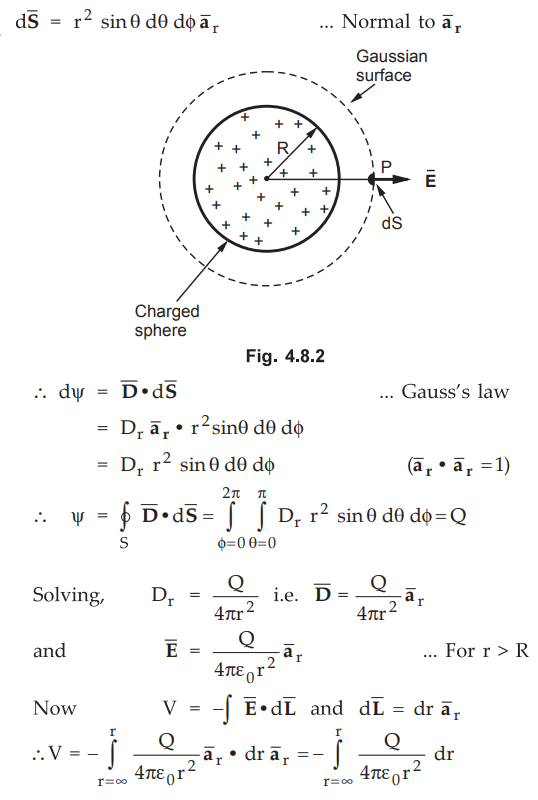
Key Point : The limits to be taken against the direction of the  i.e. from r = ∞ to r.

Ex. 4.8.2 Find the electric potential at any point given the electric field :

The boundary conditions are : at r = ∞, V = 0 and at r = 0 and V = 100.

AU : May-14, Marks 8

Sol. : The potential is given by,

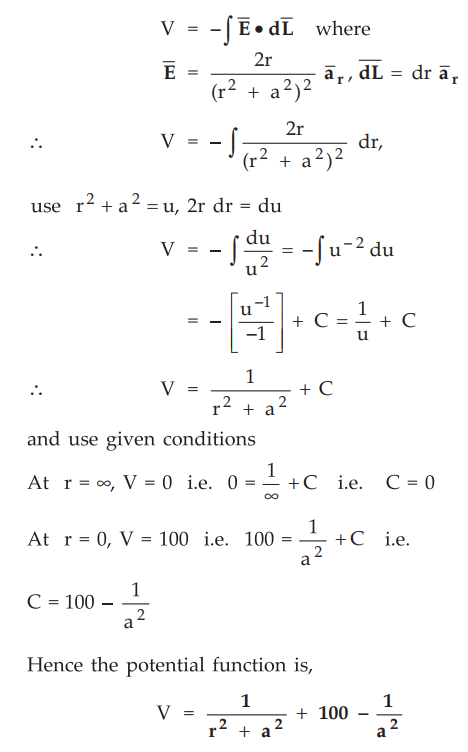
Ex. 4.8.3 If φ (r, θ, ϕ ) satisfies Laplace’s equation inside a. sphere, show that the average of φ (r, θ, ϕ ) over the surface is equal to the value of the potential at the origin.

Sol. : The value of V at a point (x, y, z) is equal to the avarage value of V around this point.

Where R = Radius of sphere

The surface integral is across the surface of a sphere centered at origin and with radius R.

Consider the electrostatic potential generated by a point charge q located on the z-axis at a distance r away from the center of a sphere as shown in the Fig. 4.8.4.

The point P is on the surface of the sphere at a distance 'd' from charge q. The potential at P is given by,

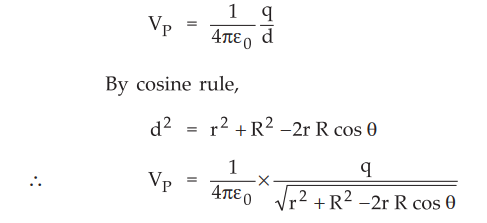
The average potential can be obtained by integrating VP across the surface of the sphere as,

This shows that the average of ^r,6,4) over the surface is equal to the value of the potential at the origin.