Potier's Triangle Method or Zero Power Factor (ZPF) Method

Potier's Triangle Method or Zero Power Factor (ZPF) Method

AU : April-96, 2000, Dec.-06, 08, May-09, 12, 13, 16, 17,18

This method is also called Potier method. In the operation of any alternator, the armature resistance drop IRa and armature leakage reactance drop IXL are actually e.m.f. quantities while the armature reaction is basically m.m.f. quantity. In the synchronous impedance all the quantities are treated as e.m.f. quantities as against this in M.M.F. method all are treated as m.m.f. quantities. Hence in both the methods, we are away from reality. 

Key Point : This method is based on the separation of armature leakage reactance and armature reaction effects. The armature leakage reactance X_L is called Potier reactance in this method, hence method is also called Potier reactance method.

To determine armature leakage reactance and armature reaction m.m.f. separately, two tests are performed on the given alternator. The two tests are,

1. Open circuit test 2. Zero power factor test

 

1. Open Circuit Test

 The experimental setup to perform this test is shown in the Fig. 2.15.1.

 The steps to perform open circuit test are,

1. The switch S is kept open.

2. The alternator is driven by its prime mover at its synchronous speed and same is maintained constant throughout the test.

3. The excitation is varied with the help of potential divider, from zero upto rated value in definite number of steps. The open circuit e.m.f. is measured with the help of voltmeter. The readings are tabulated.

4. A graph of I_f and (V_OC)_ph i.e. field current and open circuit voltage per phase is plotted to some scale. This is open circuit characteristics.

 

2. Zero Power Factor Test

To conduct zero power factor test, the switch S is kept closed. Due to this, a purely inductive load gets connected to an alternator through an ammeter. A purely inductive load has power factor of cos 90° i.e. zero lagging hence the test is called zero power factor test.

The machine speed is maintained constant at its synchronous value. The load current delivered by an alternator to purely inductive load is maintained constant at its rated full load value by varying excitation and by adjusting variable inductance of the inductive load. Note that, due to purely inductive load, an alternator will always operate at zero p.f. lagging.

Key Point : In this test, there is no need to obtain number of points to obtain the curve. Only two points are enough to construct a curve called zero power factor saturation curve.

This is the graph of terminal voltage against excitation when delivering full load zero power factor current.

One point for this curve is zero terminal voltage (short circuit condition) and the field current required to deliver full load short circuit armature current. While other point is the field current required to obtain rated terminal voltage while delivering rated full load armature current. With the help of these two points the zero p.f. saturation curve can be obtained as,

1. Plot open circuit characteristics on graph paper as shown in the Fig. 2.15.2.

2. Plot the excitation corresponding to zero terminal voltage i.e. short circuit full load zero p.f. armature current. This point is shown as A in the Fig. 2.15.2 which is on the x-axis. Another point is the rated voltage when alternator is delivering full load current at zero p.f. lagging. This point is P as shown in the Fig. 2.15.2.

3. Draw the tangent to O.C.C. through origin which is line OB as shown dotted in the Fig. 2.15.2. This is called air line.

4. Draw the horizontal line PQ parallel and equal to OA.

5. From point Q draw the line parallel to the air line which intersects O.C.C. at point R. Join RQ and join PR. The triangle PQR is called Potier triangle.

6. From point R, drop a perpendicular on PQ to meet at point S.

7. The zero p.f. full load saturation curve is now be constructed by moving a triangle PQR so that R remains always on O.C.C. and line PQ always remains horizontal. The dotted triangle is shown in the Fig. 2.15.2. It must be noted that the Potier triangle once obtained is constant for a given armature current and hence can be transferred as it is.

8. Through point A, draw line parallel to PR meeting O.C.C. at point B. From B, draw perpendicular on OA to meet it at point C. Triangles OAB and PQR are similar triangles.

9. The perpendicular RS gives the voltage drop due to the armature leakage reactance i.e. IX_L.

10. The length PS gives field current necessary to overcome demagnetising effect of armature reaction at full load.

11. The length SQ represents field current required to induce an e.m.f. for balancing leakage reactance drop RS.

These values can be obtained from any Potier triangle such as OAB, PQR and so on. So armature leakage reactance can be obtained as,

This is nothing but the Potier reactance.

 

3. Use of Potier Reactance to Determine Regulation

To determine regulation using Potier reactance, draw the phasor diagram using following procedure :

Draw the rated terminal voltage V_ph as a reference phasor. Depending upon at which power factor (cos ϕ) the regulation is to be predicted, draw the Current phasor Iph lagging or leading V_ph by angle ϕ.

Draw I_ph R_aph voltage drop to V_ph which is in phase with I_ph. While the voltage drop Iph X_L ph is to be drawn perpendicular to _Iph Raph vector but leading I_ph R_aph at the extremity of V_ph.

The R_aph is to be measured separately by passing a d.c. current and measuring voltage across armature winding. While X_Lph is Potier reactance obtained by Potier method.

Phasor sum of V_ph rated, I_ph R_aph and I_ph X_Lph gives the e.m.f. which is say E_lph. 

Obtain the excitation corresponding to E _lph from O.C.C. drawn. Let this excitation be Ffl. This is excitation required to induce e.m.f. which does not consider the effect of armature reaction.

The field current required to balanc triangle, which is say F_AR

F_AR = l (PS) = l (AC) = ...

The total excitation required is the vector sum of the F_fl and F_AR. This can be obtained exactly similar to the procedure used in M.M.F. method.

Draw vector F_fl to some scale, leading Elph by 90°. Add F_AR to F_fl by drawing vector F_AR in phase opposition to I_ph. The total excitation to be supplied by field is given by F_R

The complete phasor diagram is shown in the Fig. 2.15.3.

Once the total excitation is known which is F_R the corresponding induced e.m.f. Eph can be obtained from O.C.C. This E_ph l_ags F_R by 90°. The length CD represents voltage drop due to the armature reaction. Drawing perpendicular from A and B on current phasor meeting at points G and H respectively, we get triangle OHC as right angle triangle. Hence Elph can be determined analytically also.

Once E_ph is known, the regulation of an alternator can be predicted as,

% R = E_ph - V_ph /  V_ph × 100

This method takes into consideration the armature resistance and leakage reactance voltage drops as e.m.f. quantities and the effect of armature reaction as m.m.f. quantity. This is the reality hence the results obtained by this method are nearer to the reality than those obtained by synchronous impedance method and ampere-turns method.

The only drawback of this method is that the separate curve for every load condition is necessary to plot if potier triangles for various load conditions are required. 

 

4. Assumptions and its Effect on Accuracy in Potier Method

Assumptions made in the Potier method are,

1. In the entire calculation procedure of Potier method, the armature resistance is neglected. But practically armature resistance is very small and hence this assumption does not cause significant error in the accuracy.

2. In Potier method, a zero power factor test is required to be done. But practically when inductors are used, a perfect zero power factor can not be achieved.

3. Consider the graphical interpretation of Potier method shown in the Fig. 2.15.4.

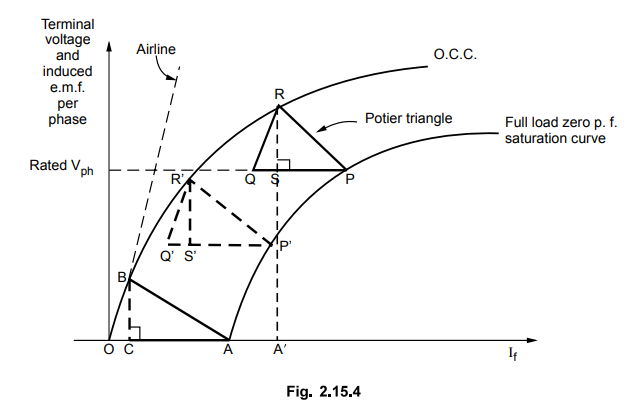
In this graph, the distances RS, R' S' and BC are assumed equal. This represents the voltage drop across the leakage reactance which is (I_aph)FL × X_Lph- This indicates that the point P in the zero power factor test and point A in the short circuit test represent same leakage reactance of the machine. But this is not true as the excitation under short circuit condition is OA while that for point P is OA' as shown. Now the excitation OA' is much higher than OC and hence point P corresponding to saturated conditions represents larger leakage flux which in the method assumed unchanged. Hence practically the leakage reactance corresponding to saturated conditions is higher than that assumed in the method. This introduces the error in the calculations 

 

Example 2.15.1 A 10 kVA, 440 V, 50 Hz, 3 phase star connected alternator has the open circuit characteristics as given below :

With full load zero p.f, the applied excitation required is 14 A to produce 500 V of terminal voltage. On short circuit, 4 A excitation is required to give full load current. Determine the voltage regulation for full load, 0.8 p.f. lagging and leading.

Solution :

Convert the given open circuit line voltages to phase voltages.

For zero p.f. saturation curve two points are given. One is short circuit full load current excitation of 4 A and terminal voltage zero. This is point A (4 A, 0 V) on x-axis. Second point If = 14 A required to get 500 V line voltage at terminals.

This gives point P (14 A, 500 / √ 3 = 288.67 V). The O.C.C. and Potier triangle is shown in the Fig. 2.15.5

From Potier triangle PQR, the armature leakage reactance drop is I (RS) = 1.1 cm.

I_ph  × X_Lph = l(RS) × scale = 1.1 × 50 = 55 V

Case i) :      cos ϕ =       0.8 lagging

Find E_{1 ph} by adding vectorially I_ph X_Lph to V_ph as shown.

Elph = 290.382 V

From O.C.C., corresponding F_fl = 6.1 A

From potier triangle, field current balancing armature reaction is l (PS).

F_AR = l(PS) × scale = 3.1 × 1 = 3.1 A

Add vectorially, F_fl and F_AR as shown in the Fig. 2.15.7.

Using cosine rule for triangle,

The corresponding voltage to FR = 8.33 A is equal to,

E_ph = 328 V ... from O.C.C.

Case ii) : cos ϕ = 0.8 leading

The drop I_ph X_Lph remains same, only its direction changes due to leading p.f. current. Find E_lph by adding I_ph X_Lph to V_ph as shown in the Fig. 2.15.8.

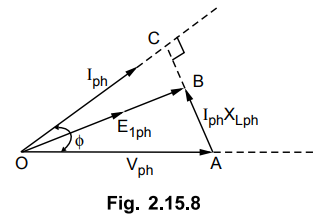
In triangle OBC,

(E_lph)² = (OC) ² + (BC) ² = (V_ph cos ϕ) ² + (V_ph sin ϕ - I_ph X_Lph)²

= (254.03 × 0.8)2 + (254.03 × 0.6 - 55)²

E_lph = 225.366 V

From O.C.C., corresponding to E_lph, F_fl = 4.1 A

F_AR = 3.1 A remains same, from Potier triangle

Add vectorially F_fl and F_AR to get F_R, as shown in the Fig. 2.15.9.

Applying cosine rule to ∆ OAB,

(FR)² = (Ffl) ² + (FAR) ² -2F_fl F_AR cos(90- ϕ)

= (4.1)² + (3.1)² - 2 × 4.1 × 3.1× cos (90 - 36.86)

F_R = 3.34 A

The corresponding open circuit voltage to F_R = 3 .34 A is equal to,

E_ph = 90 V

 

Example 2.15.2 A 11 kV, 1000 kVA, 3 phase, star connected alternator has a resistance of 2 Ω per phase. The open circuit and full load zero power factor characteristics are given below. Find the voltage regulation of the alternator for full load current at 0.8 pf. lagging by using Potier method.

Solution : The given open circuit voltages are line values hence while sketching O.C.C. convert to phase by dividing each by 1/√3

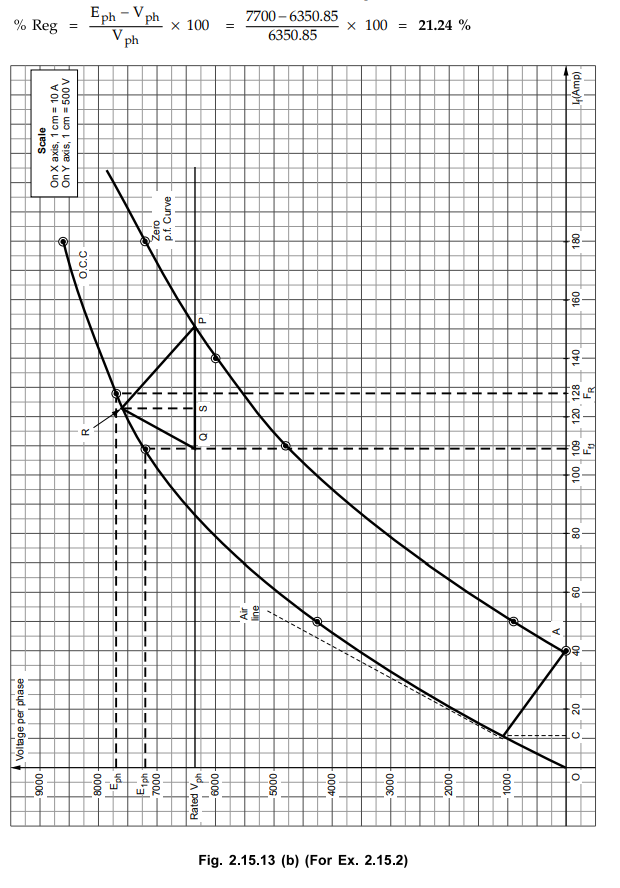
From Potier triangle PQR, shown in Fig. 2.15.13 (b), the armature leakage reactance drop is l(RS) = 2.4 cm

From O.C.C., F_f1 = 109 A

The field current for balancing armature reaction can be obtained from Potier triangle which is length PS.

F_AR = l (PS) × Scale = 2.8 × 10 = 28 A

Adding vectorially F_f1 and F_AR as shown in Fig. 2.15.13 (a).

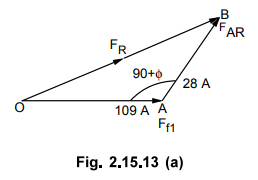
Using cosine rule for A OAB,

(OB)² = (OA) ² + (AB) ² -2(OA) (AB) cos (OA AB)

(F_R) ² = (F_f1) ² + (F_AR) ² -2 (F_f1) (F_AR) cos (90 + ϕ)

= (109) ² + (28) ² - 2 (109) (28) cos (90 + 36.86°)

(F_R) ² = 11881 + 784 - 6104 × (- 0.5998)

F_R = 127.77 A

From O.C.C. shown in the Fig. 2.15.13 (b), the corresponding E _ph is 7700 for F_R = 127.77 A

Example 2.15.3 The following data were obtained for the OCC of a 10 MVA, 13 kV, 3-phase 50 Hz, Y-connected synchronous generator.

An excitation of 100 A causes the full-load current to flow during the short-circuit test. The excitation required to give the rated current at zero pf and rated voltage is 290 A.

i) Calculate the adjusted synchronous reactance of the machine.

ii) Calculate the leakage reactance of the machine assuming the resistance to be negligible.

iii) Determine the excitation required when the machine supplies full-load at 0.8 pf lagging by using the leakage reactance and drawing the mmf phasor diagram. What is the voltage regulation of the machine ? Also calculate the voltage regulation for this loading using the adjusted synchronous reactance. Compare and comment upon the two results. AU : May-16, Marks 16

Solution : 10 MVA, 13 kV, 50 Hz, star connection

I_a(rated) = VA/√3V_L = 10 × 10⁶ /√3 × 13 ×10³ = 444 A

i) Draw O.C.C. and S.C.C. as shown in the Fig. 2.15.14.

Note that in graph line values of V_oc are used.

For rated voltage of 13 kV, calculate short circuit current from S.C.C. Corresponding to 13 kV on O.C.C. shown by point M, the short circuit current is I_sc = 690 A from graph.

ii) To find the leakage reactance, the potier triangle method must be used.

Plot the O.C.C. and locatiob of point P corresponding to ZPF at rated current. The point P is (290 A, 13 kV). This is shown in the Fig.2.15.14. Mark point A corresponding to I_f = 100 A for circulating rated I_sc . Draw line PQ = OA parallel to OA from P and locate point Q. from Q, draw line parallel to air line which intersects O.C.C. at R. Join PR. The triangle PQR is the Potier is the triangle. Draw a line RS perpendicular from R on PQ. The length RS gives the voltage drop due to the armature leakage reactance. i.e. I_XL.

iii) The length PS gives If necessary to overcome armature reaction.

l (PS) = F_AR = 3.6 cm = 90 A … from graph

Now  cos ϕ = 0.8 lagging

Find E_lph by adding vectorially (I_aph X_Lph) to V_ph.

Consider triangle OAB shown in the Fig. 2.15.14 (a).

From graph of O.C.C., field curent corresponding to E₁(line) = 13.7533 kV is F_fl = 180 A

Add vectorially Ffl and FAR as shown in the Fig. 2.15.14 (b).

Using cosine rule for the triangle OAB with

Use modified air line to obtain I_f corresponding to 19.22 kV which is line joining origin and point M. This gives linear relation between E(line) and I_f. Thus for M, E₁ (line) = 13 kV, I _f = 156 A hence for E₁(line) = 19.22 kV, I_f = 19.22 / 13 × 156 230.64  A.

From O.C.C., E_ph = 14.8 kV for I_f = 230.64 A .

%Reg. = 14.81-13 / 13 × 100 = 13.84 %

Examples for Practice

Example 2.15.4 The following table gives the open circuit and full load zero p.f. saturation characteristics data for 40 kVA, 400 V, 3 phase, 50 Hz, star connected alternator :

Find the values of armature reaction (in equivalent field current) and armature leakage reactance. Also determine the voltage regulation at 0.8 lagging pf. Neglect armature resistance.

[Ans.: 1.776 Ω 6.9 A, 20.49 A, 15.8 %]

Example 2.15.5 The following figures give the open circuit and full load zero pf.

saturation curves for a 15000 kVA, 11000 V, 3 phase, 50 Hz, star connected turboalternator.

Find the armature reaction, the armature reactance and the synchronous reactance. Deduce the regulation for full load at 0.8 pf. lagging. JNTU : March-06, Nov.-07, Feb.-08

[Ans.: 0.984 Q 6.16 Q 20.45 %] 

Review Questions

1. Explain the potier method (ZPF) of determining the regulation of an alternator.

AU : May-12,13,17,18, Dec.-06, 08, Marks 10

2. Define regulation and explain effect of power factor on regulation. Using ZPF method, calculate regulation of given alternator. Mention the advantages of this method over the other methods.