Power Flow in an Induction Motor

Power Flow in an Induction Motor   AU : May-05, 07, 10, 12, 13, Dec.-06, 07, 08, 10, 14

Induction motor converts an electrical power supplied to it into mechanical power. The various stages in this conversion is called power flow in an induction motor.

The three phase supply given to the stator is the net electrical input to the motor. If motor power factor is cos 0 and VL , IL are line values of supply voltage and current drawn, then net input electrical power supplied to the motor can be calculated as,

P_in = √3 V_L, I_L cos ϕ

where P_in = Net input electrical power

This is nothing but the stator input.

The part of this power is utilized to supply the losses in the stator which are stator core as well as copper losses. 

The remaining power is delivered to the rotor magnetically through the air gap with the help of rotating magnetic field. This is called rotor input denoted as P₂.

So P₂ = P_in - Stator losses (Core + Copper)

The rotor is not able to convert its entire input to the mechanical as it has to supply rotor losses. The rotor losses are dominantly copper losses as rotor iron losses are very small and hence generally neglected. So rotor losses are rotor copper losses denoted as

So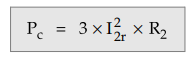 

Where         I_2r = Rotor current per phase in running condition

R₂ = Rotor resistance per phase

After supplying these losses, the remaining part of P2 is converted into mechanical which is called gross mechanical power developed by the motor denoted as P_m.

 P_m = P₂ - P_c

Now this power, motor tries to deliver to the load connected to the shaft. But during this mechanical transmission, part of P_m is utilized to provide mechanical losses like friction and windage.

And finally the power is available to the load at the shaft. This is called net output of the motor denoted as P_out. This is also called shaft power.

P_out = P_m - Mechanical losses

The rating of the motor is specified interms of value of P_out when load condition is full load condition

The above stages can ben shown diagrammatically called power flow diagram of an induction motor.

This is shown in the Fig.5.17.1.

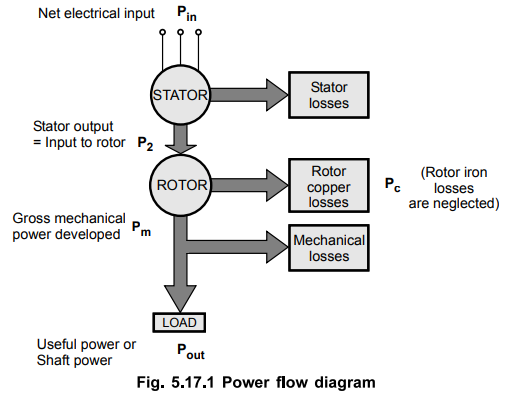
From the power flow diagram we can define,

 

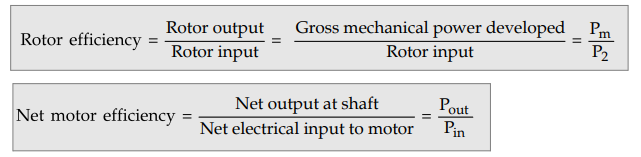
1. Relationship between P₂, P_c and P_m

The rotor input P₂, rotor copper loss P_c and gross mechanical power developed P_m are related through the slip s. Let us derive this relationship.

Let     T = Gross torque developed by motor in N-m.

We know that the torque and power are related by the relation,

P = T × w

where P = Power

and w = Angular speed = 2π N / 60 = Speed in r.p.m.

Now input to the rotor P₂ is from stator side through rotating magnetic field which is rotating at synchronous speed N_s.

So torque developed by the rotor can be expressed interms of power input P2 and angular speed at which power is inputted i.e. ws as,

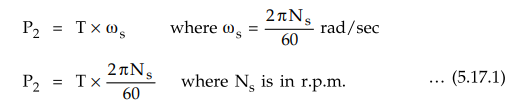
The rotor tries to deliver this torque to the load. So rotor output is gross mechanical power developed Pm and torque T. But rotor gives output at speed N and not Ns. So from output side pm and T can be related through angular speed w and not ws.

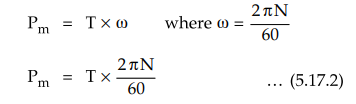
The difference between P₂ and pm is rotor copper loss Pc

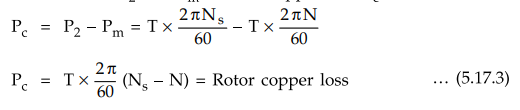
Dividing equation (5.17.3) by equation (5.17.1)

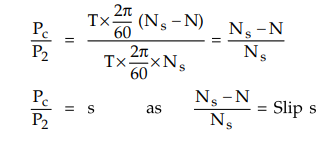
Rotor copper loss Pc = s × Rotor input P₂

Thus total rotor copper loss is slip times the rotor input.

Now P₂-Pc = Pm

P₂ - s P₂ - Pm

(1 - s) P₂ = Pm

Thus gross mechanical power developed is (1 - s) times the rotor input. The relationship can be expressed in the ratio form as,

P₂ : P_c : P_m is 1 : s : 1 - s

The ratio of any two quantities on left hand side is same as the ratio of corresponding two sides on the right hand side.

For example, P_c / P_m = s / 1 – s, P₂ / P_c  = 1/s and so on.

This relationship is very important and very frequently required to solve the problems on the power flow diagram.

Key Point The torque produced by rotor is gross mechanical torque and due to mechanical losses entire torque cannot be available to drive load. The load torque is net output torque called shaft torque or useful torque and is denoted as T_sh- It is related to P_out as,

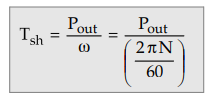
and T_sh < T due to mechanical losses

Derivation of k in Torque Equation

We have seen earlier that

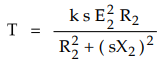
and it is mentioned that k = 3 /2πn_s Let us see its proof.

The rotor copper losses can be expressed as,

 

2. Efficiency of an Induction Motor

The ratio of net power available at the shaft (P_out) and the net electrical power input (P_in) to the motor is called as overall efficiency of an induction motor.

%ƞ = P_out / P_in × 100

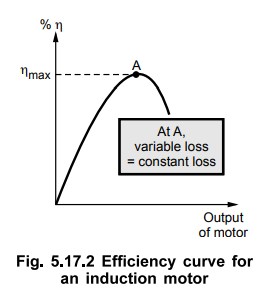
The maximum efficiency occurs when variable losses become equal to constant losses. When motor is on no load, current drawn by the motor is small. Hence efficiency is low. As load increases, current increases so copper losses also increase. When such variable losses achieve the same value as that of constant losses, efficiency attains its maximum value. If load is increased further, variable losses become greater than constant losses hence deviating from condition for maximum, efficiency starts decreasing. Hence the nature of the curve of efficiency against output power of the motor is shown in the Fig. 5.17.2.

Example 5.17.1 The useful torque of a 3 phase, 50 Hz, 8 pole induction motor is 190 Mn. The rotor frequency is 1.5 Hz. Calculate the rotor copper losses if mechanical losses are 700 walts.

 

Example 5.17.2 A 415 V, 3 phase, 50 Hz, 4 pole, star connected induction motor runs at 24rev/s on full load. The rotor resistance and reactance per phase are 0.35 ohm and 3.5 ohm respectively and the effective rotor-stator turns ratio is 0.85 : 1. Calculate :

1) Slip

2) The full load torque

3) The power output if the mechanical losses amount to 770 W

4) The maximum torque

5) The speed at which the maximum torque occurs and

6) The starting torque.

Solution :

 

Example 5.17.3 A 100 kW (output), 3300 V, 3 phase, star connected induction motor has a synchronous speed of 500 r.p.m. The full load slip is 1.8 % and full load power factor 0.85. Stator copper loss - 2440 W. Iron loss - 3500 W. Rotational losses - 1200 W. Calculate 1) The rotor copper loss 2) The line current 3) The full load efficiency. AU : Dec.-07, Marks 8

Solution :

Example 5.17.4 A 3 phase, 440 V, 50 Hz, 40 pole, Y-connected induction motor has rotor resistance of 0.1 Ω and reactance 0.9 Ω per phase. The ratio of stator to rotor turns is 3.5. Calculate gross output at a slip of 5 %, and the maximum torque in syn. watts and corresponding slip.

Solution :

 

Example 5.17.5 An 18.65 kW, 4 pole, 50 Hz, 3 phase induction motor has friction and windage losses of 2.5 percent of the output. Full load slip is 4 %. Find for full load 1) Rotor copper loss 2) Rotor input 3) Shaft torque 4) the gross electromagnetic torque. AU : Dec.-06, 10, Marks 8

Solution :

 

Example 5.17.6 The real power input to a 415 V, 50 Hz, 6 pole, 3-phase induction motor running at 970 rpm is 41 kW. The input power factor is 0.9. The stator losses amount to 1.1 kW and the mechanical losses total 1.2 kW. Calculate the line current, slip, rotor copper loss, mechanical power output and efficiency.

Solution :

 

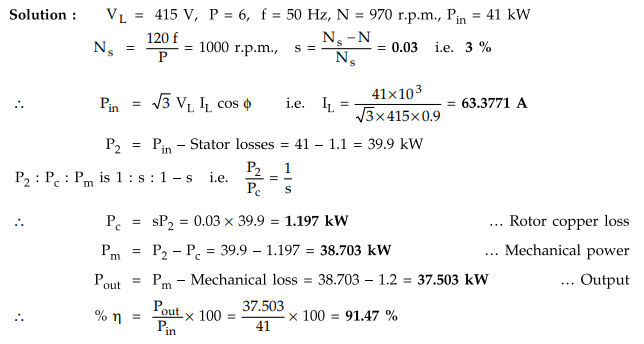
Example 5.17.7 An eight pole, 3-phase induction motor running with the slip of 4 % takest 20 kW from a 50 Hz supply. Stator losses amount to 0.5 kW. If the mechanical torque lost in friction is 16.2 Nm. Find the power output and efficiency.

Solution :

 P = 8, s = 0.04, P_in = 20 kW, f = 50 Hz

Stator losses = 0.5 kW, T_lost = 16.2 Nm

 

Example 5.17.8 An induction motor has an efficiency of 0.9 when the shaft load is 45 kW. At this load, stator ohmic loss and rotor ohmic loss each is equal to the iron loss. The mechanical loss is one-third of the no-load losses. Neglect ohmic losses at no-load. Calculate the slip.

Solution :

Rotor iron losses are negligible due to low rotor frequency.

Stator copper loss         = Rotor copper loss = Stator iron loss = W_i

 

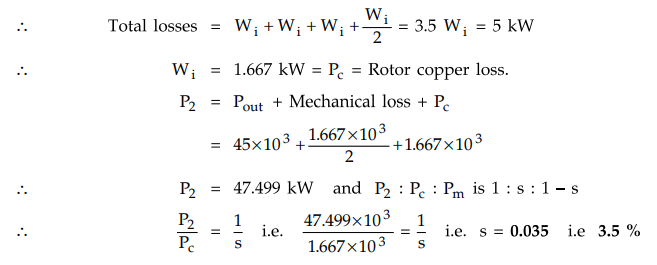
Examples for Practice  

Example 5.17.9 The power input to a 3 phase 50 Hz induction motor is 50 kW. The total stator loss is 800 W. Find the total mechanical power developed, if the rotor emf makes 90 complete cycles per minute.

[Ans.: P_m = 47724 W]

Example 5.17.10 A 6-pole, 50 Hz, 3-^ induction motor running on full load develops a useful torque of 150 Nm at a rotor frequency of 1.5 Hz. Calculate the shaft power output. If the mechanical torque lost in friction be 10 Nm, determine: i) Rotor copper loss ii) The input to the motor iii) The efficiency.

[Ans.: i) 502.6548 W, ii) 17455.16 W, iii) 87.29 %] 

Example 5.17.11 A 3 phase, 4 pole, 50 Hz, star connected induction motor running on full load develops a useful torque of 300 N-m. The rotor e.mf. is completing 120 cycles per minute. If torque lost in friction is 50 Nm, calculate : i) Slip ii) Net output power iii) Rotor copper loss per phase iv) Rotor efficiency and v) Rotor resistance per phase if rotor current is 60 A in running condition.

[Ans.: i) 4 %, ii) 45.2389 kW, iii) 733.0378 W, iv) 96 %, v) 0.2036 n/ph]

Example 5.17.12 A 3 phase, 4 pole, 50 Hz induction motor is supplied by 400 V supply. Its full load slip is 4 %. At full load, stator copper losses are same as rotor copper losses. Stator iron losses are 25 % more than stator copper losses. Mechanical losses are one third of no load losses. Full load output is 50 h.p. Calculate the efficiency on full load.      

[Ans.: % ^ = 85.77 %]

Example 5.17.13 An I.M. has an efficiency of 0.9 when the load is 50 H.P. At this load, stator copper loss and rotor copper loss is each equal to the iron loss. The mechanical losses are one-third of the no load losses. Calculate the slip.

[Ans.: s = 0.03 i.e. 3 %]

Example 5.17.14 A squirrel-cage induction motor is rated 25 kW, 440 V, 3-0, 50 Hz. On full-load it draws 28.7 kW with line current 50 A and runs at 720 rpm. Calculate :

i) The slip (s) ii) The power factor, and iii) The efficiency (ƞ). UPTU : 2013-14

[Ans.: i) 4 %, ii) 0.7532 lagging, iii) 87.108 %]

Example 5.17.15 A3- ϕ, 400 V, 6-pole, 50Hz, IM, develops mechanical power of 20 kW at 985 rpm. Calculate :

i) The rotor copper loss, ii) The total input power, and iii) Rotor frequency (f₂)

The stator losses are equal to 1800 W. Neglect mechanical loss.

UPTU : 2013-14

[Ans.: i) P_c = 0.3045 kW, ii) P_in = 22.1045 kW, iii) f₂ = 0.75 Hz]

Example 5.17.16 A 25 kW, 4 pole, 3 phase, 50 Hz induction motor is running at 1410 r.p.m., supplying full load. The mechanical losses are 850 W and stator losses are 1.7 times rotor copper losses on full load. Calculate ,

i) Gross mechanical power developed

ii) Rotor copper losses

iii) The value of rotor resistance per phase if rotor current on full load per phase is 65 A

iv) The full load efficiency.

[Ans.: 25850 W, 1650 W,0.13 n per phase, 82.49 %] 

Example 5.17.17 A 6 pole 50 Hz, 3 phase, induction motor running on full load with 4 % slip develops a torque of 149.3 Nm at its pully rim. The friction and windage losses are 200 W and the stator copper and iron losses are equal to 1620 W. Calculate :

i) Output power ii) The rotor copper losses iii) The efficiency at full load.

VTU : July-11, Aug.-05

[Ans. : 15209.2 W, 633.7166 W, 87.094 %]

Example 5.17.18 A 6 pole, 3-phase induction motor develops 30 HP including mechanical losses, total 2 HP at a speed of 950 rpm on 550 V, 50 Hz mains. The power factor is 0.58. Calculate for this load i) slip ii) the rotor copper loss iii) the total input if the stator losses are 2000 W iv) the efficiency v) the line current vi) the number of complete cycles of the rotor e.m.f. per minute.

[Ans.: 5 %, 1238.736 W, 26774.736 W, 82.409 %, 31.938 A, 150 cycles/min]

Example 5.17.19 A 25 HP, 6 pole, 50 Hz, slip ring induction motor runs at 960 rpm on full load, with a rotor current of 35 A. Allowing 250 W for the copper loss in the short circuiting gear and 1000 W for mechanical losses, find the resistance per phase of the 3-phase rotor winding.

[Ans. : 0.1546 Ω]

Review Questions

1. Discuss the different power stages of a 3 phase induction motor with losses with the help of a power flow diagram.

2. Derive the relation between refer input rotor copper losses of mechanical power developed in terms of a slip of a three phase induction motor.