Power Flow in Synchronous Motor

Power Flow in Synchronous Motor

Net input to the synchronous motor is the three phase input to the stator.

P_in = √3 V_L I_L cosϕ W

where V_L = Applied line voltage 

I_L = Line current drawn by the motor

cos ϕ = Operating p.f. of synchronous motor

or P_in = 3 (per phase power) = 3 × V_ph I_aph cos ϕ W

Now in stator, due to its resistance R_a per phase there are stator copper losses.

Total stator copper losses = 3 × (I_aph)²  × R_a W

The remaining power is converted to the mechanical power, called gross mechanical power developed by the motor denoted as P_m.

P_in  = P_in - Stator copper losses

Now  P = T  × W

P_m = T_g × 2π N_S / 60 a speed is always N_S

T_g = P_m × 60 / 2π N_S

This is the gross mechanical torque developed. In d.c. motor, electrical equivalent of gross mechanical power developed is E_b × I_a, similar in synchronous motor the electrical equivalent of gross mechanical power developed is given by,

P_m =  3 E_bph × I_aph × cos (E_bph Λ I_aph)

i) For lagging p.f.,  E_bph Λ I_aph = ϕ - δ

ii)      For lagging p.f.,   E_bph Λ I_aph = ϕ + δ

iii)     For unity p.f.,   E_bph Λ I_aph =  δ

Note : While calculating angle between E_bph and I_aph from phasor diagram, it is necessary to reverse Ebpb phasor. After reversing Ebpb, as it is in opposition to V_ph, angle between E_bph and I_aph must be determined.

In general,

P_m =  3 E_bph  I_aph  cos (ϕ ± δ )

Positive sign for leading p.f. and Negative sign for lagging p.f.

Net output of the motor then can be obtained by subtracting friction and windage i.e. mechanical losses from gross mechanical power developed.

P_out = P_m - mechanical losses.

 T_shaft = P_out × 60 / 2π N_S  Nm

where T_shaft = shaft torque available to load

P_out = Power available to load

% ƞ P_out / P_in × 100  … Overall efficiency

The power flow in synchronous motors can be summarized as shown in the Fig. 4.13.1

Example 4.13.1 A 9 kW, 400 V three phase star connected synchronous motor has synchronous impedance per phase of (0.4 + 3j) Ω. Find the angle of retard and the voltage to which the motor must be excited to give a full-load output at 0.8 leading power factor. Assume an efficiency of 90 %.

Solution :

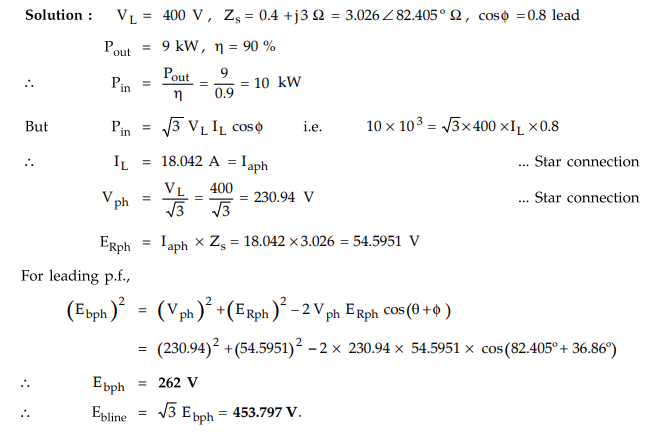
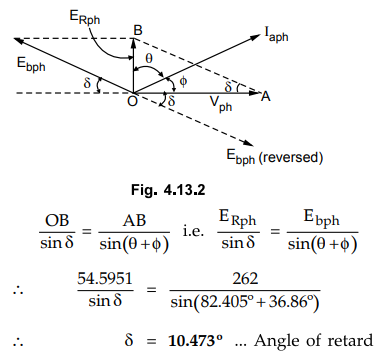
The phasor diagram is shown in the Fig. 4.13.2.

To find angle of retard δ , apply sine rule to ∆ OBA

Example 4.13.2 A three phase 500 V, star connected synchronous motor gives net output of 17 kW on full load operating at 0.9 lagging power factor. Its armature resistance is 0.8 Ω per phase. The mechanical losses are 1300 W. Estimate the current drawn by the motor and full load efficiency.

Solution :

Example 4.13.3 A 75 kW, 400 V, 4-pole, 3-phase, star-connected synchronous motor has a resistance and synchronous reactance per phase of 0.04 Ω and 0.4 Ω respectively. Compute for full load 0.8 pf lead the open-circuit e.m.f. per phase and gross mechanical power developed. Assume an efficiency of 92.5 %.

Solution :

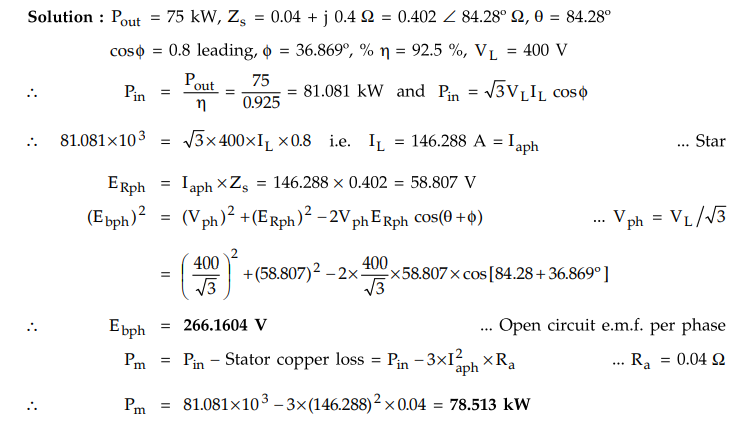
Alternatively, P_m = 3E_bphI_aph cos(ϕ + δ) for which δ must be calculated. Students may calculate δ and use the above expression to calculate P_m. For reference, δ = 10.89°.

Example 4.13.4 A 3-phase star-connected synchronous motor rated at 187 kVA, 2300 V, 47 A, 50 Hz, 187.5 rpm has an effective resistance of 1.5 Ω and a synchronous reactance of 20 Ω per phase. Determine the internal power developed by the motor when it is operating at rated current and 0.8 power factor leading.

Solution :

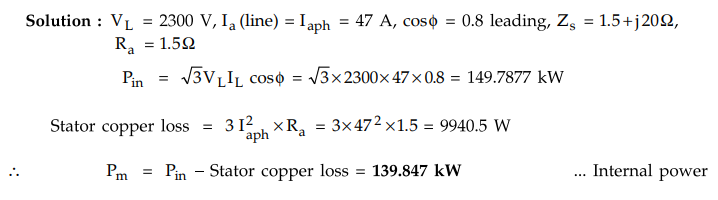
Examples for Practice

Example 4.13.5 A 6600 V, three phase, star connected synchronous motor draws a full load current of 80 A at 0.8 pf. leading. The per phase armature resistance is 2.2         Ω and synchronous reactance is 22 Ω. If the stray losses of machine are 3200 watt, calculate the induced e.m.f, output power and efficiency. UPTU : 2005-06

[Ans.: 4962.1625 V, 686.1782 kW, 93.78 %]

Example 4.13.6 A 20-kW, 400-V, 3-phase, star-connected synchronous motor has per phase impedance of (0.15 + j 0.90) Ω. Determine the induced emf torque angle and mechanical power developed for full load at 0.8 pf lagging. Assume 92 % efficiency of the motor. Draw phasor diagram.

[Ans.: 206.534 V, 6.1414°, 21.04 kW]

Review Question

1. Explain the power flow in synchronous motor with the help of power flow diagram.