Power Flow through Transmission Line

Power Flow through Transmission Line

AU : Oct.-98, May-10, 11, 15, Dec.-15, 17

The flow of power at any point along a transmission line can be determined with the knowledge of voltage, current and power factor. This power can be derived in terms of the transmission or ABCD parameters. These equations can be applied to any two terminal pair network.

Fig. 2.14.1 shows a transmission line with sending end quantities represented by subscript 'S' and receiving end quantities represented by subscript 'R'.

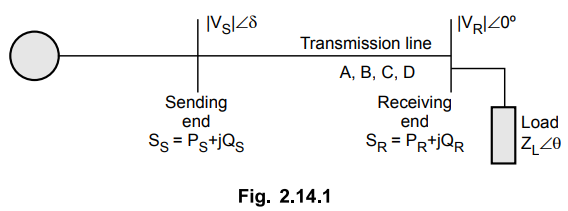
The complex power delivered by the receiving end and that received by the sending end of the transmission line is given as,

S_R = P_R + jQ_R = V_R I_R

S_S = P_S + jQ_S = V_S I_S

Here I_R and I_S are complex conjugate of currents I_R and I_S.

Consider the Fig. 2.14.2.

Consider the following equation for sending end voltage in terms of ABCD parameters.

The receiving end power will be maximum when P=8 as seen from above equation. Substituting  β = δ in the expression for P_R we get

The corresponding Q_R when P_R is maximum is given by,

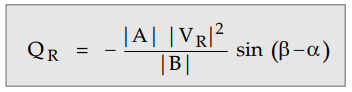
Thus maximum real power will be received if the load draws the leading reactive power given by above equation.

Thus it can be seen that there is limit to the power that can be transmitted to the receiving end of the line for specified magnitudes of sending and receiving end voltages. When angle δ becomes equal to β, maximum power will be transferred or delivered. Further increase in δ results in less power received.

For achieving the condition of maximum power the load must draw a large amount of leading current which is not practicable. But by using leading VAR compensation the power transfer can be improved.

1. Power Flow through Short Transmission Line

Consider a short transmission line with series impedance Z. The shunt admittance of the line is negligible. The ABCD parameters for short transmission line are

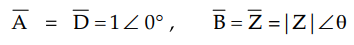
Substituting these values in expressions for P_R and Q_R obtained in previous section we get, 

The equations that are written for short transmission line can also be applied for a long line when the line is replaced by its equivalent n model and the shunt admittances are lumped with the load at receiving end and sending end generation.

From the above equation for P_R, it can be seen that maximum power is received at receiving end when δ  = θ such that

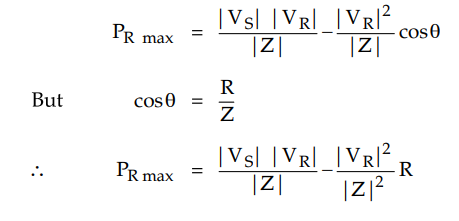
Normally resistance of a transmission line is small as compared to its reactance which is necessary to maintain efficiency of line high

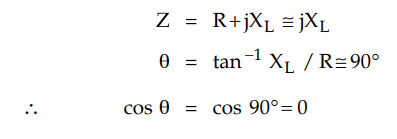
Thus by neglecting R the expressions for P_R and Q_R will reduce to

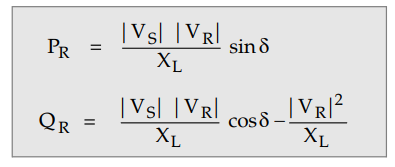
For stability considerations equation for P_R is helpful while equation for Q_R plays important role in reactive power compensation.

In practice angle δ is between 15 to 30° So that cos 8 lies between 0.966 and 0.866. If we assume 8 = 1 we will get reactive power supplied by short line to receiving end as given by,

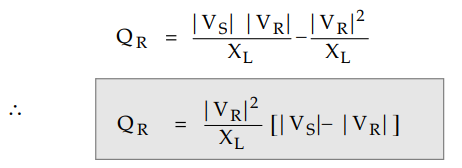
The difference between sending end and the receiving end voltage is say AV

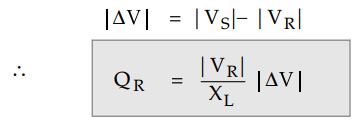
Various important observations can be obtained which are as follows :

1. For small R (R ≅ 0) and for small δ, the real power transferred to the receiving end is proportional to sin δ while the reactive power is proportional to the magnitude of the voltage drop across the line.

2. Maximum real power transferred is maximum when δ = 90° and the magnitude of this maximum power is | V_S | |V_R| /X_L. sin= sin 90° = 1 is called steady state stability limit.

3. Maximum power at receiving end is proportional to V2. Hence for higher power transfer, corresponding voltage must also be higher.

4. Reactive power delivered by line Q_R is dependent on AV and is independent of power angle δ.

Consider the equation for a short transmission line that we have already considered

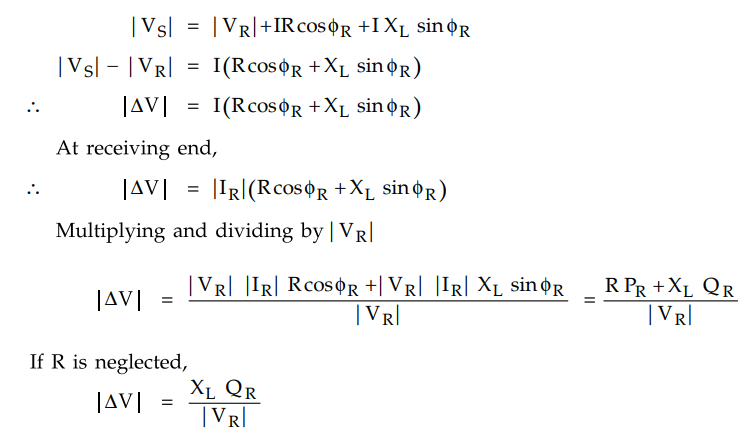
This expression we had obtained previously. Thus the voltage drop | ΔV | in the line is determined by the series reactance X_L of the line and the reactive power delivered by the line at receiving end i.e. Q_R.

If reactive power Q_R is injected at receiving end, the line voltage drop | ΔV | can be reduced. This is called reactive power compensation during high loads. From this equation it can also be seen that larger power can be transmitted over a line with fixed voltages by providing compensation at the receiving end.

Example 2.14.1 The sending and receiving end voltages of a 3 phase transmission line are maintained at 33 kV and 31.2 kV respectively. The resistance and reactance per phase are 20 and 50 ohms respectively. Determine the maximum power obtainable at the receiving end.

Solution : Since the capacitance of the line is not mentioned it is neglected. Hence the line is treated as short transmission line. The ABCD parameters are given by,

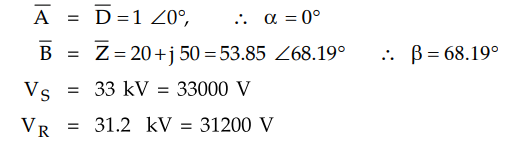
The expression for maximum power is given by

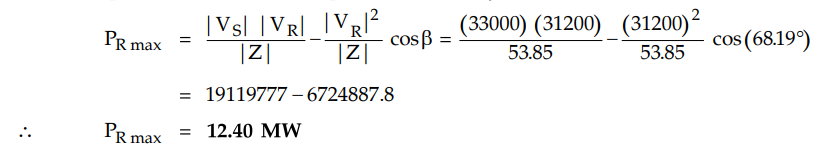
Review Question

1. Deduce an expression for the sending end and receiving end power of a line in terms of voltages and ABCD constants. Show that the real power transferred is dependent on the power angle and reactive power transferred is dependent on the voltage drop in the line.

AU : May-10, 11, 15, Dec.-15, 17, Marks 16