Poynting Vector and Poynting Theorem

Poynting Vector and Poynting Theorem

AU : May-04, 06, 07, 10, 11, 12, 17,18, Dec.-03, 04, 06, 07, 08, 09, 10, 11, 12, 14, 17, 19

• By the means of electromagnetic (EM) waves, an energy can be transported from transmitter to receiver. The energy stored in an electric field and magnetic field is transmitted at a certain rate of energy flow which can be calculated with the help of Poynting theorem. As we know  and  are basic fields.  is electric field expressed in V/m; while  is magnetic field measured in A/m. So if we take product of two fields, dimensionally we get a unit V.A/m² or watt/m². So this product of   and  gives a new quantity which is expressed as watt per unit area. Thus this quantity is called power density.

Statement of poynting theorem

• Poynting theorem states that the vector product of electric field intensity   and magnetic field intensity  at any point is a measure of the rate of energy flow per unit area at that point and the direction of power flow is perpendicular to   and  both along the direction of .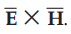

As   and  both are vectors, to get power density we may carry out either dot product or cross product. The result of a dot product is always a scalar quantity. But as power flows in certain direction, it is a vector quantity. To illustrate this, consider that the field is transmitted in the form of an electromagnetic waves from an antenna. Both the fields are sinusoidal in nature. The power radiated from antenna has a particular directon. Hence to calculate a power density, we must carry out a cross product of   and . The power density is given by

• Where  is called Poynting Vector, named after an English Physicist John N. Poynting.  is the instantaneous power density vector associated with the electromagnetic (EM) field at a given point. The direction of  indicates instantaneous power flow at the point. To get a net power flowing out of any surface, is integrated over same closed surface.

• The Poynting theorem is based on law of conservation of energy in electromagetism. Poynting theorem can be stated as follows :

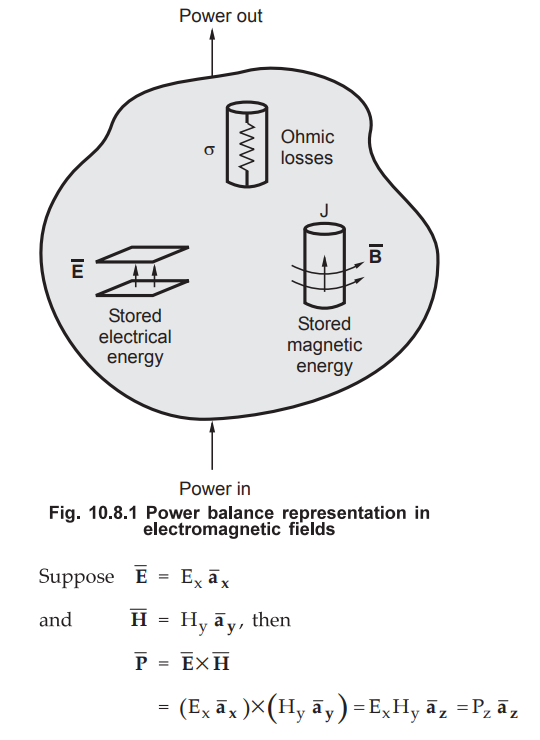
• The net power flowing out of a given volume v is equal to the time rate of decrease in the energy stored within volume v minus the ohmic power dissipated. This can be well illustrated by the Fig. 10.8.1.

• The above equation indicates that 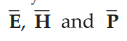 are mutually perpendicular to each other. 

• Consider that the electric field propagates in free space given by

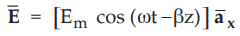
• In the medium, the ratio of magnitudes of   and   depends on its intrinsic impedance ɳ. For free space,

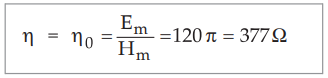
• Moreover, in the free space, electromagnetic wave travels at a speed of light.

• Thus we can write,

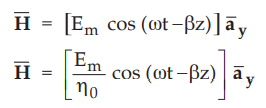
• According to Poynting theorem

• This is nothing but the power density measured in watt/m². Thus the power passing particular area is given by,

Power = Power density × Area

1. Average Power Density (P_avg)

• To find average power density, let us integrate power density in z-direction over one cycle and divide by the period T of one cycle.

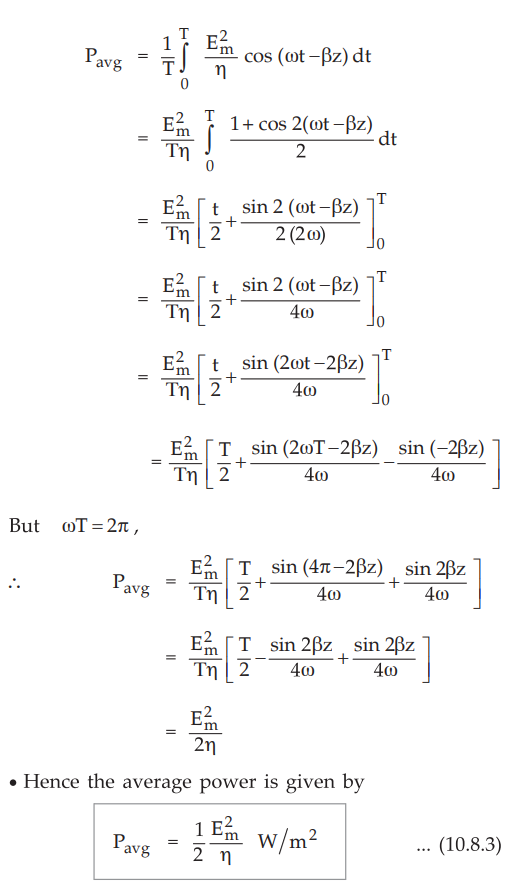
• The average power flowing through any area S normal to the direction of power flow is given by,

 

2. Integral and Point Forms of Poynting Theorem

• Consider Maxwell's equations as given below:

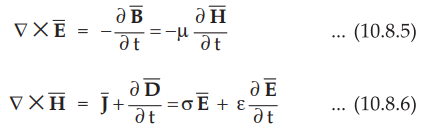
 • Dotting both the sides of equation (10.8.6) with  , we get,

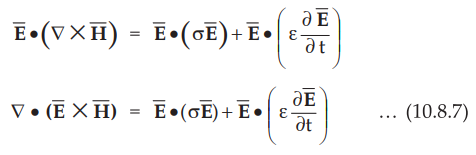
• Let us make use of a vector identity as given below,

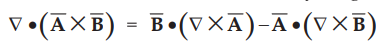
• Applying above vector identity to equation (10.8.8) with

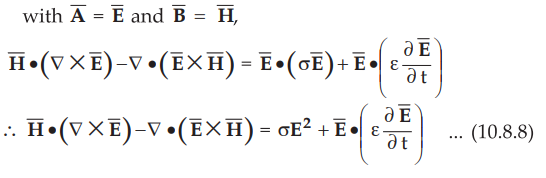
• Consider first term on left of equation (10.8.8). Putting value of  from equation (10.8.5) we can write,

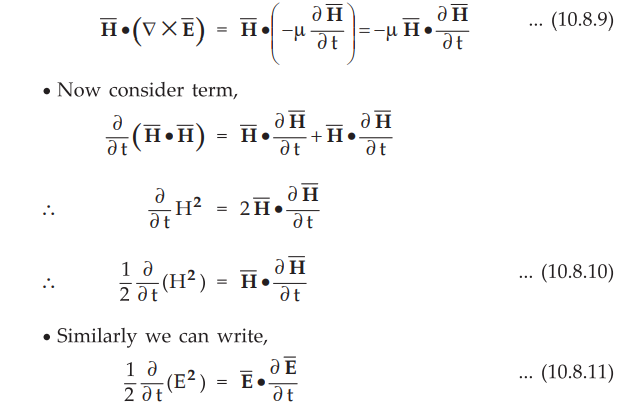
• Using results obtained in equations (10.8.9), (10.8.10) and (10.8.11) in equation (10.8.8),

• Equation (10.8.12) represents Poynting theorem in point form. If we integrate this power over a volume, we get energy distribution as,

• Applying divergence theorem to left of above equation, we get,

• Equation (10.8.13) represents Poynting theorem in integral form.

Inerpretation of the terms in the equation

1. The term on the left-hand side indicates the net power flowing out of the surface. The term  is poynting vector and is equal to 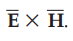. It is the instantaneous power density vector associated with the electromagnetic field at any point.

2. The first term on the right-hand side represents power dissipated in the medium where σ ≠ 0. It is actually the total ohmic power loss within the volume. 

3. The second term on the left hand side represents the rate of decrease in energy stored in the electric and magnetic fields.

4. According to the law of conservation of energy, the sum of two terms on the right-hand side is equal to the total power flowing out of the volume. This can be interpreted as,

• This can be represented with the help of equation as given below,

• When we define Poynting vector, both the fields  and  are assumed to be in the real form. If  and  are expressed in phasor form, then the average power is given by,

 

3. Power Flow in Co-axial Cable

• Consider a co-axial cable in which the power is transfered to the load resistance R along a cable. There are two conductors namely inner conductor and outer conductor concentric to each other. Let the radius of the inner conductor be 'a' units and the inner radius of the outer conductor be 'b' units as shown in the Fig. 10.8.2.

• In the cable, there exists a d.c. voltage V between the two conductors, while the steady current I flows in the inner and outer conductors as shown in the Fig. 10.8.2. The magnetic field strength H will be directed in the circular path about the axis as shown in the Fig. 10.8.2. In the region between the two conductors, the current enclosed is equal to the magnetomotive force around any of the circles of H.

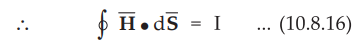
• The magnetic field H is constant along any of the circular path. Let r be the radius of any circle considered then the magnetomotive force is given by,

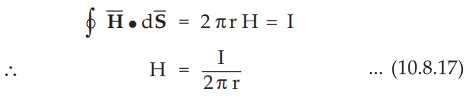
• Let q be the charge per unit length, then the potential difference between inner and outer conductor of a co-axial cable is given by,

V = q / 2πƐ log (b/a) … (10.8.18)

• Similarly the magnitude of electric field intensity E for a co-axial cable is given by,

E = q / 2πƐr

• From equations (10.8.18) and (10.8.19), we can write,

E = q / r [log(b/a)] …(10.8.20),

• According the Poynting theorem, the Poynting vector is given by,

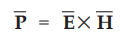
• But the power flows in the direction parallel to the axis of the cable. As E and H are mutually perpendicular to each other everywhere, the magnitude of the Poynting vector is given by,

P = E • H

• The total power flow along the cable can be obtained by integrating the Poynting vector over any cross-sectional surface with area 2 π r dr.

• Above result is certainly an universal result the power flow is product of voltage and current. The important point to be noted here that the area over which the Poynting vector is integrated did not include any of the conductors. Hence we can conclude that in case of a perfect conductor, the power flow is entirely external to the conductors.

 

4. Instantaneous, Average and Complex Poynting Vector

• In electromagnetic field theory, the relations between the Poynting vector and the field strength are very much similar to those relations between power and voltage and current in a.c. circuits.

• In general, the Poynting vector is given by

• Equation (10.8.22) represents the instantaneous power flow per unit area. Hence it is also called instantaneous Poynting vector.

• The complex Poynting vector is given by,

• From equation (10.8.23) it is clear that the product of  and  is a vector product. The mutually perpendicular components of  and , contribute to the power flow. This power flow is directed along the normal to the plane containing  and . Thus the complex flow of power per unit area normal to the x-y plane is given by

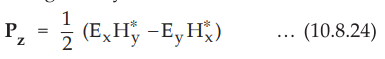
• Using the complex Poynting vector, we can obtain the average and reactive parts of the power flow per unit area.

• The average part of the power flow per unit area is given by

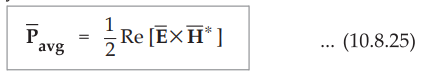
• Similarly the reactive part of the power flow per unit area is given by

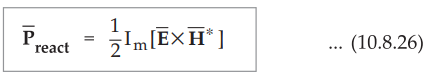
• In terms of the complex Poynting vector, the total instantaneous Poynting vector can be written as,

 

5. Power Loss in a Plane Conductor

• The power loss in a conductor is nothing but the power flow per unit area through the surface. Such a power flow from the surface is represented by the normal component of the Poynting vector at the surface of the conductor.

• Let us consider a plane metallic conductor with a thickness greater compared to the skin depth 8 of the conductor. The skin depth of a conductor is defined as a distance through which the amplitude of the travelling wave decreases to 37 % of the original amplitude.

• Let 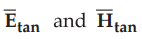 be the tangential components of the electric field  and the magnetic field  at the surface of the conductor respectively. According to the continuity requirement, the tangential component of  is continuous at the boundary of the conductor. Then the tangential component of the electric field  is obtained from the relationship given by,

η = E_tan / H_tan ... (10.8.28)

where η = Intrinsic impedance of the conductor

• Hence just inside the conductor the tangential component of  is given by,

E_tan  = η H_tan ...(10.8.29)

• According to the continuity requirements, outside the conductor surface the tangential component of  will be same.

• The average power flow per unit area normal to the surface is given by,

• The tangential components of   and  are at right angles to each other. But for a good conductor E_tan leads Htan by 45°, equation (10.8.30) can be modified as,

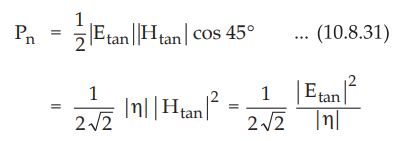
• As we have assumed that the thickness of the conductor is much greater than the skin depth, it can be considered that surface impedance Zs is equal to the intrinsic impedance n of the conductor. Then equation (10.8.31) can be written as,

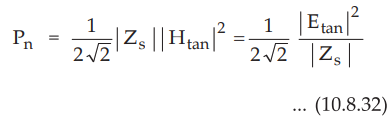
• The current density  in a conductor is proportional to the magnetic field strength at the surface.

• In the equations (10.8.31), (10.8.32) and (10.8.33) the values of E_tan, H_tan and Js are assumed to be the maximum values. If these values are expressed as effective or r.m.s. values then the equations are given by,

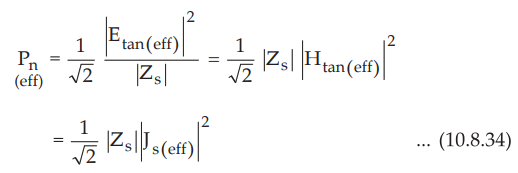
• Equations (10.8.31), (10.8.32), (10.8.33) and (10.8.34) represent the normal component of the Poynting vector i.e. the power loss in a conductor.

 

Ex. 10.8.1 In free space, 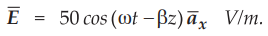Find the average power crossing a circular area of radius 2.5 m in the plane z = 0. Assume E m = Hm . η0 and η0 = 120π Ω . AU : May-07, Marks 8

Sol. : In complex form,

The power flow is normal to the circular area.

 

Ex. 10.8.2 In free space

E(z,t) = 100 sin(ωt- βz)  (V/m). Find the total power passing through a square area of side 25 mm in the z = 0 plane.

Sol. :

Hence total power passing through area of square of side 25 mm is given by,

P = (P_avg) (Area)=(13.2629) (25× 10⁻³)² = 8.289 mW

 

Ex. 10.8.3 A plane travelling wave has a peak electric field intensity E as 6 kV/m. If the medium is lossless with Ɛr =3 andµr =1, find the velocity of the EM wave, Poynting vector, impedance of the medium and the peak value of the magnetic field H.

Sol. : E0 = Peak electric field = 6 kV/m

For lossless medium : Ɛ r = 3, µr = 1

i) For the lossless medium, the velocity of EM wave is given by,

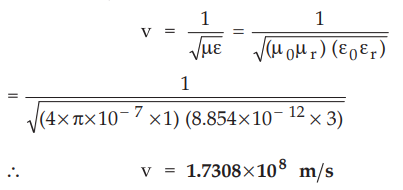
ii) The intrinsic impedance of the lossless medium is given by,

 

Ex. 10.8.4 Give the physical significance of Poynting vector. A uniform plane wave 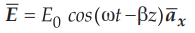 is propagating in medium. Find the magnitude and direction of Poynting vector. Calculate the average power density and the average power flowing through circular area of radius a in xy plane.

AU : May-05, Marks 8

Sol. : Consider that the electromagnetic wave is propagating in free space. The electric field is given by'

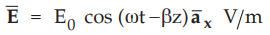
For the free space, the ratio of magnitudes of  depends on the intrinsic impedance i.e. h o which is given by,

η₀ = E₀ / H₀ = 377 Ω

Thus we can write the expression for  which is mutually perpendicular to   as,

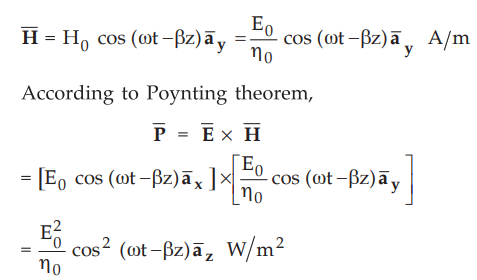
To find average power density, integrating power density over one cycle and divided by period T of one cycle, we get,

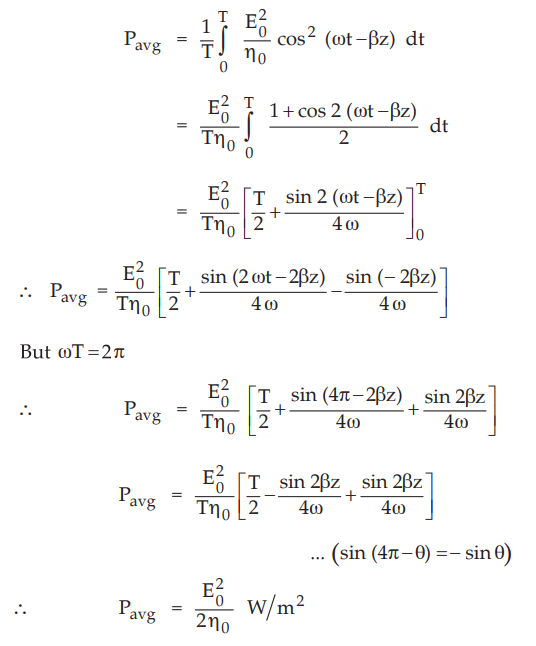
Now the circular area with radius a is given by,

Area = πr² = πa²

Hence the power flowing through the circular area of radius a in x-y plane is given by,

 

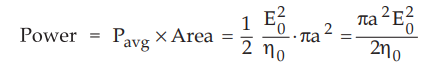
Ex. 10.8.5 A circularly polarized electromagnetic wave is given by :

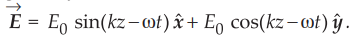
Show that the average value of the Poynting vector for the wave is equal to the sum of the Poynting vectors of its components.

Dec.-19, Marks 13

Sol. : The electrical field is given by,

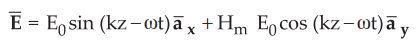
As the wave is propagating in the z direction, the corresponding magnetic field is given by,

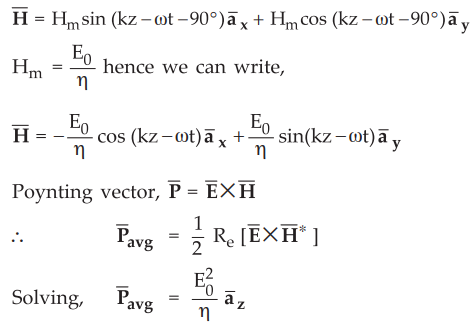
The individual components having average poyning vectors are given by,

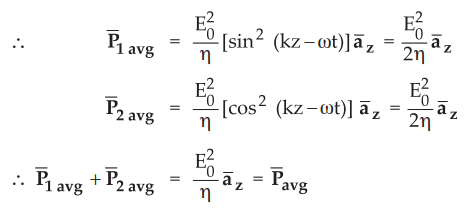
This show that average value of poynting vector for the wave is equal to the sum of the poynting vectors of its components.

 

Examples for Practice

Ex. 10.8.6 If the field vectors of a wave in free space are given by,

Determine the phasor Poynting vector and calculate power crossing 4 m² patch of the y-z plane.

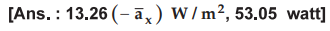
Ex. 10.8.7 In free space, .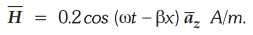

 Find the total power passing :

i)  a square plate of side 10 cm on plane x + z = 1

ii) a circular disc of radius 5 cm on plane x = 1.

[Ans.: 53.3144 mW, 59.2176 mW]

Review Questions

1. State and prove Poynting's theorem and derive the expression for average power.

AU : May-04, 06, 10, 17, Dec.-04, Marks 12

2. A charge q is moving with a uniform velocity v . Obtain its poynting vector and show that the energy propagates along with the moving charge.

AU : Dec.-08, 19, Marks 13

3. Derive suitable relations for integral and point forms of Poynting theorem.

4. Define and derive Poynting vector. Mention its practical significance.

AU : May-07, 18, 19, Dec.-03, 12, 17, Marks 8

5. Explain Poynting vector and power flow in electromagnetic fields.

6. Explain the following : Poynting vector, average power and instantaneous power.

AU : Dec.-lO, May-12, Marks 8

7. Show that the total power flow along a coaxial cable will be given by the surface integration of the poynting vector over any closed surface.

AU : May-06, 11, Dec.-06, 14, Marks 12