Problems based on analytic function necessary conditions – cauchy - riemann equations

PROBLEMS BASED ON ANALYTIC FUNCTION NECESSARY CONDITIONS – CAUCHY - RIEMANN EQUATIONS

Example 3.1.1. Show that the function f (z) = xy + iy is continuous everywhere but not differentiable anywhere.

Solution:

Given: f (z) xy + iy

i.e., u = xy, v = y

x and y are continuous everywhere and consequently u (x, y) = xy and v (x, y) = y are continuous everywhere.

Thus f (z) is continuous everywhere.

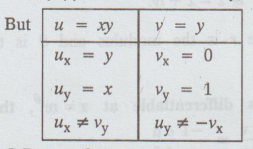
C-R equations are not satisfied.

Hence, f(z) is not differentiable anywhere though it is continuous everywhere.

 

Example 3.1.2. Show that the function f(z) =  is nowhere differentiable. [A.U N/D 2012]

Solution:

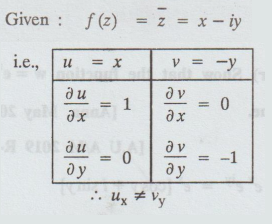
C-R equations are not satisfied anywhere.

Hence,  is not differentiable anywhere (or) nowhere differentiable.

 

Example 3.1.3. Show that f(z) = | z |² is differentiable at z = 0 but not analytic  at z = 0. [Anna, May 1996, A/M 2008]

Solution :

So, the C-R equations ux = Vy and u1 = -Vx, are not satisfied everywhere  except at z = 0.

So, f (z) may be differentiable only at z = 0.

Now, u1 = 2x, uy = 2y, v, = 0 and vy = 0 are continuous everywhere and  in particular at (0, 0).

Hence, the sufficient conditions for differentiability are satisfied by f (z) at z = 0.

So, f (z) is differentiable at z = 0 only and is not analytic there.

 

(c) Inverse functions

Let w = f (z) be a function of z and z = F(w) be its inverse function.

Then the function w = f (z) will cease to be analytic at points dz/dw = 0 and

z  = F(w) will be so, at points where dw / dz = 0

 

Example: 3.1.4 If w = e^z, find dw / dz. (or) Show that the function w = e^z is analytic everywhere in the complex plane.

Solution :

 Let z = x + iy

 Here, ux = Vy and uy = - vx

Further ex, cos y, sin y are continuous and so ux, Vx, uy and vy are continuous everywhere.

Thus the sufficient conditions for the existence of derivative of e2 are satisfied everywhere.

 

Example 3.1.5. Check for the analyticity of log z.

 (OR)

Show that f(z) = log z is analytic everywhere except at the origin and find its derivatives.

Solution:

Let z = re^iθ

f(z) = log z

= log (re^iθ) = logr + log (re^iθ) = logr + iθ

But, at the origin, r = 0. Thus, at the origin,

f(z) = log 0 + iθ  = - ∞ + iθ

Note : e^{- ∞} = 0

log ^{- ∞} = log 0

- ∞ = l0g 0

So, f (z) is not defined at the origin and hence is not differentiable there.

At points other than the origin, we have

So, log z satisfies the C-R equations.

Further 1/r is not continuous at z = 0.

So, u_r, u_θ, v_r v_θ are continuous everywhere except at z = 0. Thus log z satisfies all the sufficient conditions for the existence of the derivative except at the origin. The derivative is

 

Example 3.1.6. Check whether w =  is analytic everywhere.

Solution:

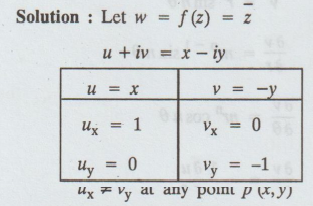
Hence, C-R equations are not satisfied.

The function f (z) is nowhere analytic.

 

Example 3.1.7. Test the analyticity of the function w = sin z.

Solution:

Let w = f(z) = sin z

u + iv = sin (x + iy)

u + iv = sin x cos iy + cos x sin iy

u + iv = sin x cosh y + i cos x sinh y

Equating real and imaginary parts, we get

C-R equations are satisfied.

Sub Also the four partial derivatives are continuous.

Hence, the function is analytic.

 

Example 3.1.8. Test the analyticity of the function f(z) = zⁿ and find its derivative.

Solution:

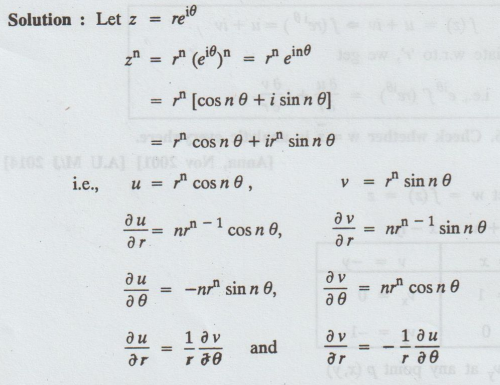
C-R equations are satisfied and the partial derivatives are continuous.

Hence, the function is analytic.

 

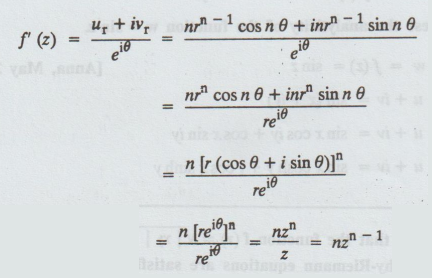
Example 3.1.9. Show that f(z) = 1/z is analytic everywhere except at z = 0 and find f' (z).

Solution:

 

Example 3.1.10. Show that the function f(z) = √| xy | is not regular at the origin, although Cauchy-Riemann equations are satisfied at the origin.

Solution :

The limit is not unique, since it depends on m.

f' (0) does not exist.

Hence, f (z) is not regular at the origin.

 

Example 3.1.11. Determine whether the function 2xy + i (x² - y²) is analytic or not.

Solution:

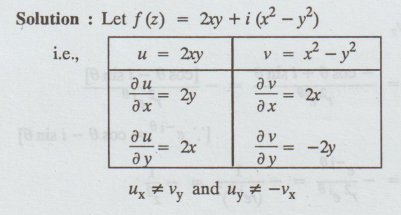
C-R equations are not satisfied.

Hence, f (z) is not an analytic function.

 

Example 3.1.12. Show that the function x² + iy³ is not analytic anywhere. How do you explain the fact that C-R equations are satisfied at x = 0, y = 0.

Solution:

C-R equations are not satisfied.

Ind visas Hence, f (z) is not analytic.

2x = 3y2 is true at x = 0, y = 0

Hence, C-R equations are satisfied at (0,0).

 

Example 3.1.13. If f (z) = (x − y)² + 2i (x + y), show that the C-R equations are satisfied along the curve x - y = 1.

Solution:

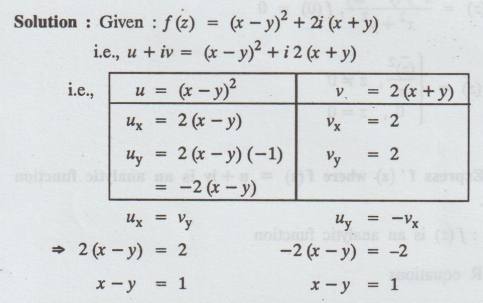
Hence, C-R equations are satisfied only if x - y = 1.

 

Example 3.1.14. Prove that f(z) = cosh z is an analytic function and find its derivative.

Solution: Given: f(z) = cosh z = cos (iz)  = cos [i (x + iy)]

= cos (ix - y) = cos ix cos y + sin (ix) sin y

 

Example 3.1.15. Give an example that the C-R equations are necessary but not sufficient to be analytic.

Solution:

 

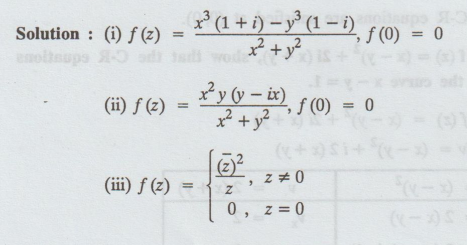
Example 3.1.16. Express f' (z) where f (z) = u + iv is an analytic function in different ways.

Solution: Given: f (z) is an analytic function

 

Example 3.1.17 If u + iv is analytic, show that viu and -v + iu are also analytic.

Solution: Given: u + iv is analytic

⇒ C-R equations are satisfied.

i.e., Ux = Vy … (1)

and uy = -Vx … (2)

Since, the derivatives of u and v exist therefore it is continuous.

Now, to prove viu and -v + iu are also analytic, we should prove that

 (i) vx = -uy and vy = ux and

(ii) –vx = uy and vy = ux

 (iii) ux, Uy, Vx and vy all are continuous. Results (i) and (ii) follows from (1) and (2). Since the derivatives of u and v exists from (1) and (2), the derivatives of u and v should be continuous.

Hence, the result (iii) follows.

 

Example 3.1.18 If w = f (z) is analytic, prove that dw/dz = ∂w/∂x = - I ∂w/∂y where z = x + iy. and prove that   [Anna, Nov 2001]

Solution :

Let w = u (x,y) + iv (x,y)

As f (z) is analytic, we have u_x = v_y, u_y = -v_x

 

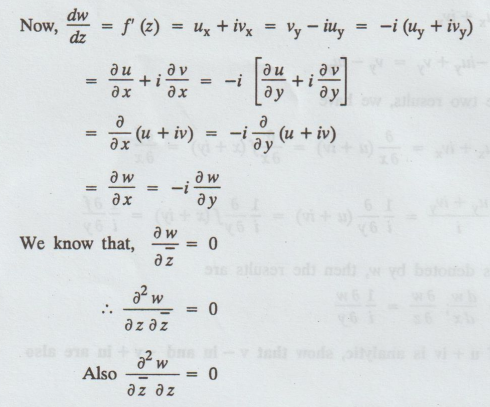
Example 3.1.19. Prove that every analytic function w = u(x, y) + iv (x, y) can be expressed as a function of z alone. [A.U. M/J 2010, M/J 2012]

Hence, u and v and also w may be considered as a function of z and 

i.e., w is a function of z alone.

This means that if w = u(x, y) + iv (x, y) is analytic, it can be rewritten as a function of (x + iy).

Equivalently a function of  can not be an analytic function of z.

 

Example 3.1.20. Show that u + iv = x - iy  / x - iy + a (a ≠ 0) is not an analytic function of z, where as u - iv is such a function at all points where z ≠ - a.

Solution:

 

Example 3.1.21. Find the constants a, b, c if f(z) = (x + ay) + i (bx+cy) is analytic.

Solution :

 

Example 3.1.22. If f(z) = r² (cos 2 θ + i sin p θ) is analytic, then find the value of 'p'. [A.U A/M 2018 R-17]

Solution

 

Example 3.1.23. Examine whether the following function is analytic or not. f(z) = e^-x (cos y - i sin y)

Solution: Given: f(z) = e^-x (cos y - i sin y)

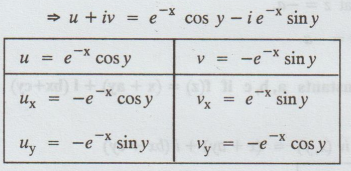
Here, u_x = v_y and u_y = -v_x

⇒ C-R equations are satisfied

⇒ f (z) is analytic.

 

Example 3.1.24. Test whether the function

f(z) = log (x² + y²) + i tan^-1 (y/x) is analytic or not.

Solution:

Here, u_x = v_y and u_y = -v_x

⇒ C-R equations are satisfied

⇒ f(z) is analytic.

 

Example 3.1.25. For what values of z, the function w defined by z = e^-v (cos u + i sin u) ceases to be analytic.

Solution: The function w = f (z) will cease to be analytic at points, where dz/dw = 0

z = e^-v e^iu = e^{i (u + iv)}

z = e^iw

dz / dw = e^iw = iz = 0 when z = 0

Thus w ceases to be analytic at z = 0.

 

Example 3.1.26. Find where each of the following functions ceases to be analytic. (i) z / (z² – 1) + i (ii) z + i / (z – i) ²  (iii) tan² z

Solution: