Probability and complex function: Unit IV: Complex integration
Problems based on cauchy's integral formula
Complex integration
Probability and complex function: Unit IV: Complex integration : Problems based on cauchy's integral formula
(b) PROBLEMS
BASED ON CAUCHY'S INTEGRAL FORMULA
Example 4.1.b.1
Evaluate 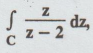 where C is [z]=3.[A.U M/J 2014]
where C is [z]=3.[A.U M/J 2014]
Solution:
We know that, Cauchy's integral formula is
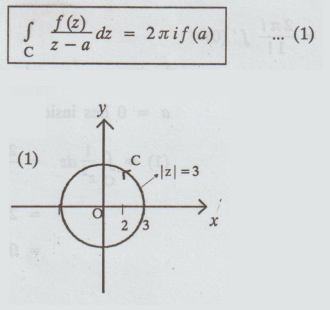
Given:
f(z) = z, a = 2, C is | z | = 3
a
= 2 lies inside | z | = 3
f
(a) = f(2) = 2
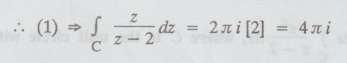
Example 4.1.b.2
Evaluate 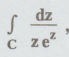 where C is | 1 | = 3
where C is | 1 | = 3
Solution: We
know that, Cauchy's integral formula is
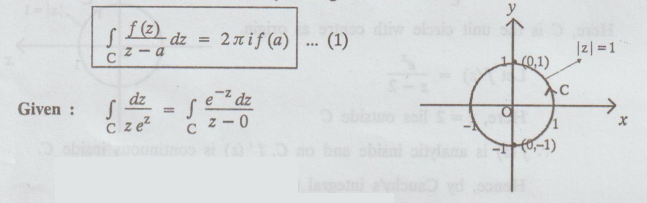
Here,
f (z) = e-z
a
= 0 is lies inside | z | = 1
f
(a) = f (0) = e-0 = 1
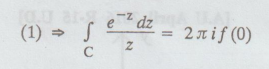
=
2 πi (1) = 2 πi
Example 4.1.b.3
Evaluate  over the
entire complex plane. [A.U N/D 2019 (R17)]
over the
entire complex plane. [A.U N/D 2019 (R17)]
Solution:
We know that, Cauchy's integral formula is
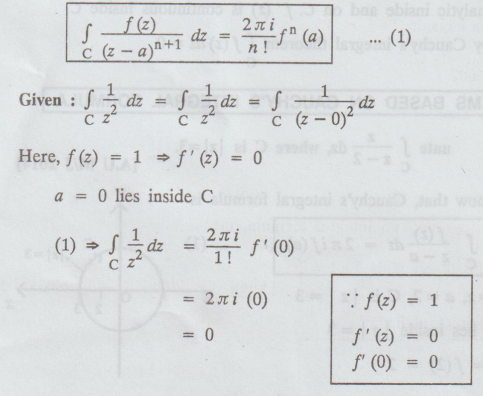
Example 4.1.b.4. Evaluate 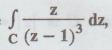 where C is | z|= 2, using Cauchy's integral formula.
[Anna, May 1998]
where C is | z|= 2, using Cauchy's integral formula.
[Anna, May 1998]
Solution: We
know that, Cauchy's integral formula is

Example 4.1.b.5.
Evaluate 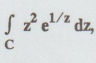 where C is | z | = 1 [Anna, May 2001]
where C is | z | = 1 [Anna, May 2001]
Solution:
Given: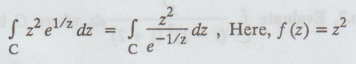
z
= 0, we get e-1/0 = e-∞ = 0
z
= 0 lies inside | z | = 1
Cauchy's
integral formula is
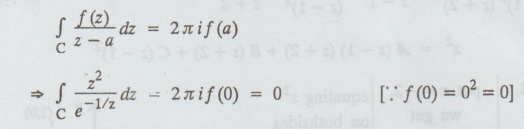
Example 4.1.b.6 Using
Cauchy's integral formula, evaluate 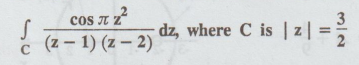 [Anna, Oct. 1997 & May
2001]
[Anna, Oct. 1997 & May
2001]
Solution : Cauchy's
integral formula is
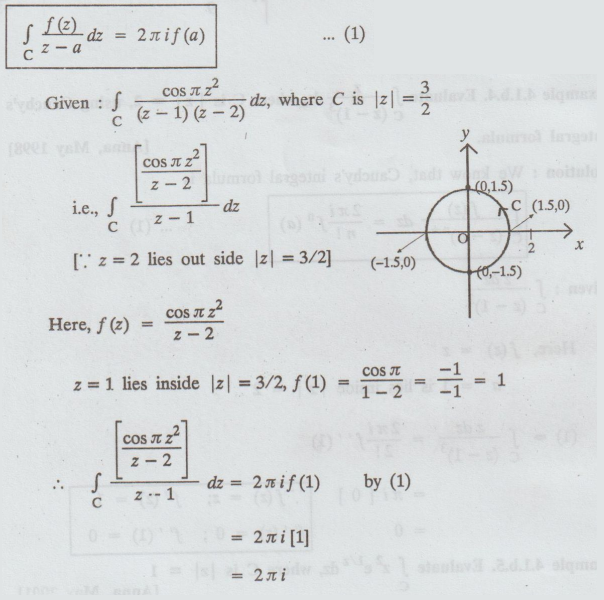
Example 4.1.b.7.
Evaluate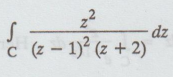 where C is |z❘
= 3 [A.U A/M 2015 R-13]
where C is |z❘
= 3 [A.U A/M 2015 R-13]
Solution : z
= 1 lies inside | z❘
= 3
z
= -2 lies inside ❘z❘ = 3
z2
/(z - 1)2 (z + 2) =A/z – 1 + B/(z - 1)2 + C/ z + 2
......(1)
z2
= A (z − 1) (z + 2)+ B (z + 2) + C(z - 1)2
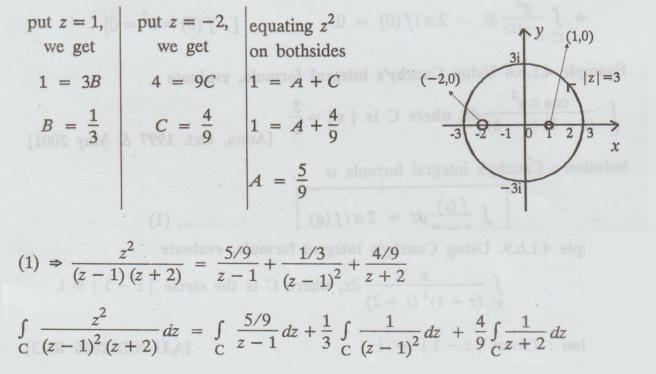
=
(5/9)2π if (1) + 1/3 2π if' (1) + 4/9 2π if (-2) by Cauchy's integral formula
=
(5/9)2π (1) + 1/3 2π (0) + 4/9 2π (1) [f(z)
= 1]
=
2πi [ 5/9 + 4/9 ] = 2πi
Example
4.1.b.8 Evaluate 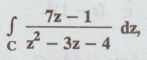 where C is ellipse x2+4y2
= 4.
where C is ellipse x2+4y2
= 4.
Solution : Cauchy's
integral formula is

Example 4.1.b.9. Using
Cauchy's integral formula, evaluate 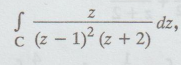 where C is the circle| z
- 1|= 1 [A.U N/D 2016 R-13]
where C is the circle| z
- 1|= 1 [A.U N/D 2016 R-13]
Solution:
Given | z - 1|= 1
Here,
centre 1, radius 1
z
= 1 lies inside C : | z -1 |=1
z
= -2 lies outside C:| z - 1| = 1
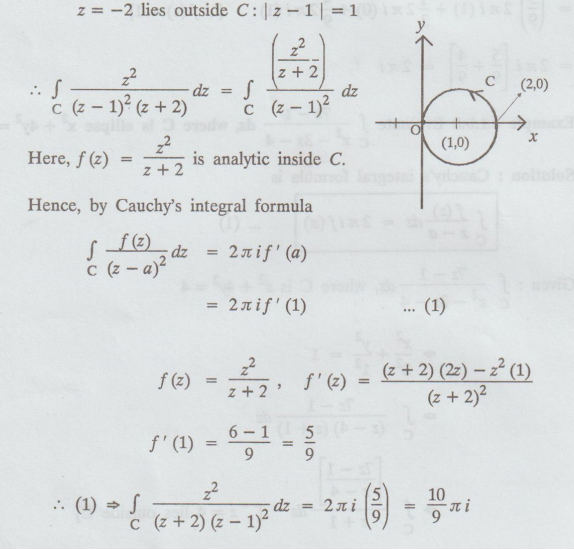
Example
4.1.b.10.Evaluate 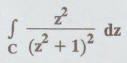 where C is the circle |z –i |= 1 by using
Cauchy's integral formula. [A.U A/M 2018, R-17]
where C is the circle |z –i |= 1 by using
Cauchy's integral formula. [A.U A/M 2018, R-17]
Solution :
Cauchy's
integral formula is
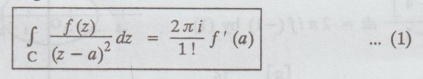
Given:
| z – i |= 1 is a circle, whose centre is (0, 1) and radius is 1.
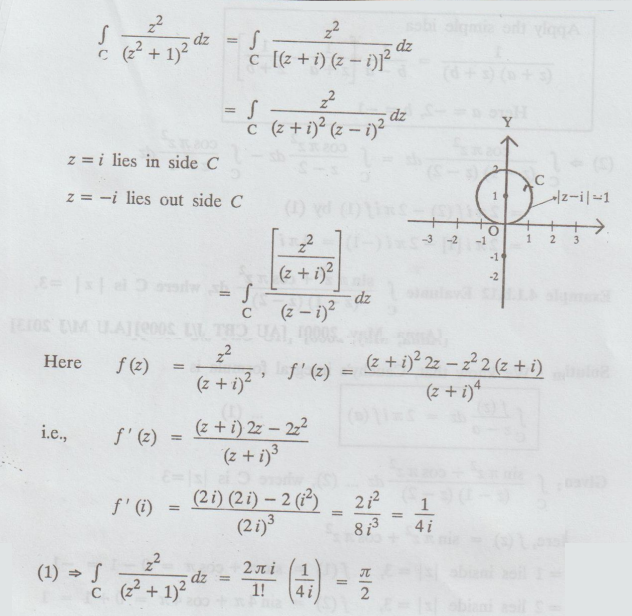
Example 4.1.b.11.
Evaluate 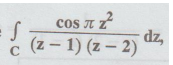 where C is | z | = 3.
where C is | z | = 3.
Solution : Cauchy's
integral formula is
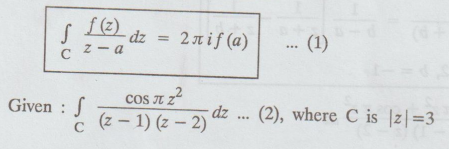
Here,
f (z) = cos л z2
z
= 1 lies inside | z | = 3, f (1) = cos л = -1
z
= 2 lies inside | z | = 3, ƒ (2) = cos 4 π = 1
Consider,
1/ (z - 1) (z - 2) = 1/(z - 2)(z - 1) = [ 1/z – 2 + 1/ z – 1]
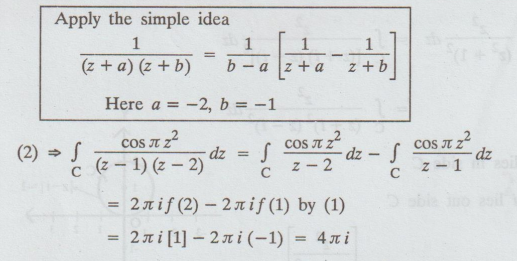
Example
4.1.b.12 Evaluate 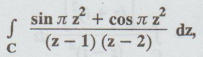 dz, where C is | z | = 3.
dz, where C is | z | = 3.
[Anna,
May, 2000] [AU CBT J/J 2009] [A.U M/J 2013]
Solution:
We
know that, Cauchy's integral formula is

Example
4.1.b.13. Evaluate using Cauchy's integral formula 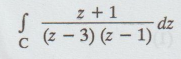 where C is the
circle | z | = 2. [A.U M/J 2016 R-13]
where C is the
circle | z | = 2. [A.U M/J 2016 R-13]
Solution:
Given:
| z | = 2
⇒ Centre 0, radius = 2
z
= 3 lies outside | z | = 2; z = 1 lies inside | z | = 2
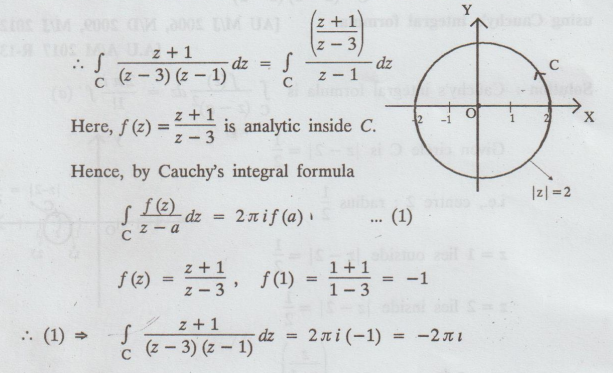
Example
4.1.b.14. Evaluate 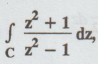 dz where C is | z – 1 | = 1, using
Cauchy’s integral formula.
dz where C is | z – 1 | = 1, using
Cauchy’s integral formula.
Solution
: Cauchy's integral formula is

Example
4.1.b.15. Evaluate 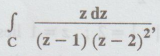 where C is |z – 2| = by using Cauchy's integral
formula.
where C is |z – 2| = by using Cauchy's integral
formula.
[AU
M/J 2006, N/D 2009, M/J 2012]
Solution
:
Cauchy's integral formula is

Example
4.1.b.16. Using Cauchy's integral formula, evaluate
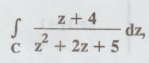 where C is the circle | z + 1 - i | = 2
where C is the circle | z + 1 - i | = 2
[A.U,
Nov. 2001, N/D 2007]
Solution:
Given:
|
z + 1 - i | = 2 i.e., | z-(-1+ i) | = 2
is
a circle whose centre is -1+ i and radius is 2.
i.e.,
centre is (-1, 1) and radius is 2.
Consider,
z2 + 2z + 5 = 0
Hence,
by Cauchy's integral formula
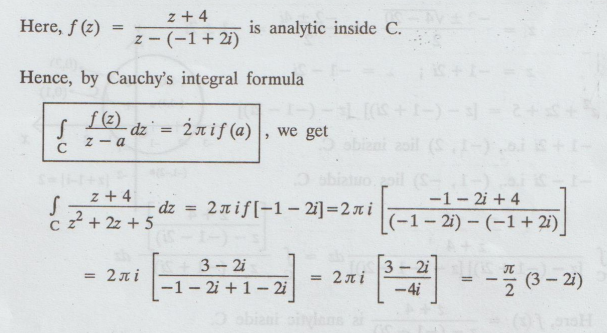
Example
4.1.b.18. Evaluate  dz where C is | z + 1+ i | = 2
dz where C is | z + 1+ i | = 2
using
Cauchy's integral formula. [A.U. A/M 2011] [A.U N/D 2013 R-8]
Solution
: z2 + 2z + 4 = 0
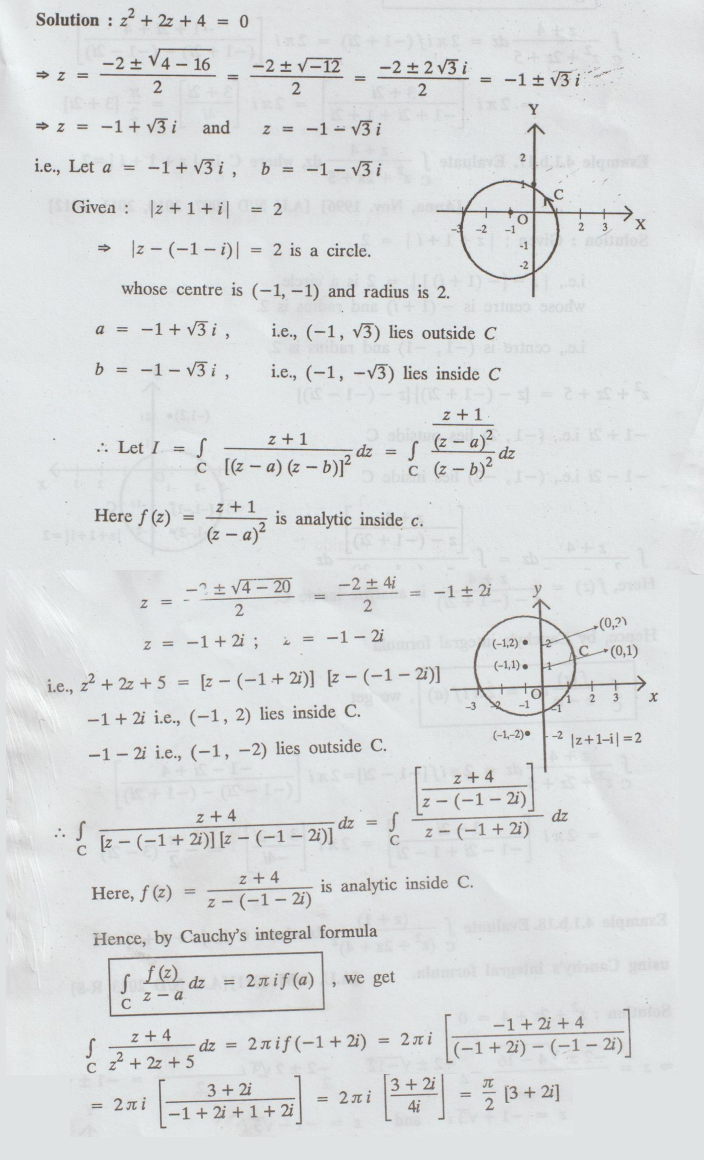
Example
4.1.b.17. Evaluate 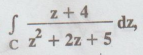 where C is | z + 1 + I | = 2
where C is | z + 1 + I | = 2
[Anna,
Nov. 1996] [A.U N/D 2007, 2010, 2011, 2012]
Solution:
Given: | z + 1 + i | = 2
i.e.,
| z - [ - (1 + i)] | = 2 is a circle
whose
centre is - (1 + i) and radius is 2.
i.e.,
centre is (-1, -1) and radius is 2.
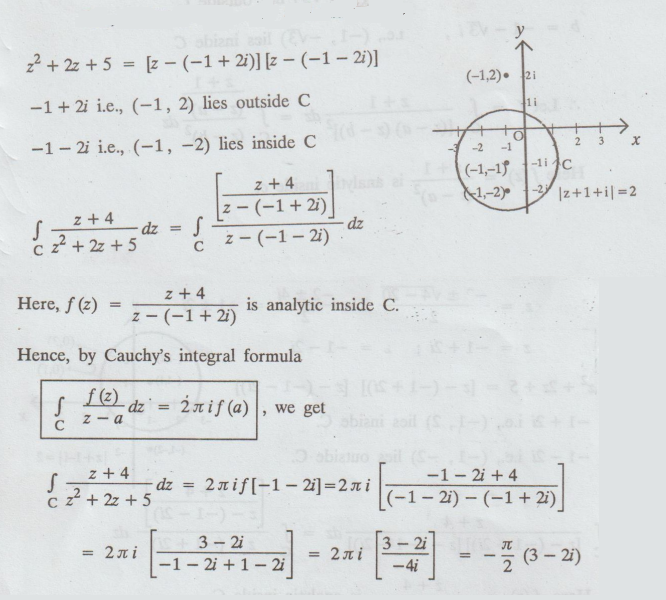
Example
4.1.b.18. Evaluate 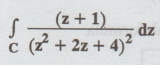 dz where C is ❘z
+ 1 + i | = 2 using Cauchy's integral formula. [A.U. A/M 2011] [A.U N/D 2013
R-8]
dz where C is ❘z
+ 1 + i | = 2 using Cauchy's integral formula. [A.U. A/M 2011] [A.U N/D 2013
R-8]
Solution:
z2 + 2z + 4 = 0

Example
4.1.b.19. Evaluate 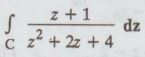 where C is the circle | z + 1+ i | = 2
using Cauchy's integral formula. [A.U N/D 2016 R-8] [A.U N/D 2014 R-13]
where C is the circle | z + 1+ i | = 2
using Cauchy's integral formula. [A.U N/D 2016 R-8] [A.U N/D 2014 R-13]
Solution
:
Given:
|
z + 1 + i | = 2
|
z - (-1 - i)| = 2 is a circle,
where
centre is -1- i and radius is 2.
i.e.,
centre (-1, -1) and radius is 2.
z2+
2z + 4 = 0

Example
4.1.b.20. If 'c' is the circle | z | = 3 and if
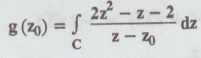 then g(2)
then g(2)
[A.U
A/M 2018, R-17]
Solution:
We
know that, Cauchy's integral formula is
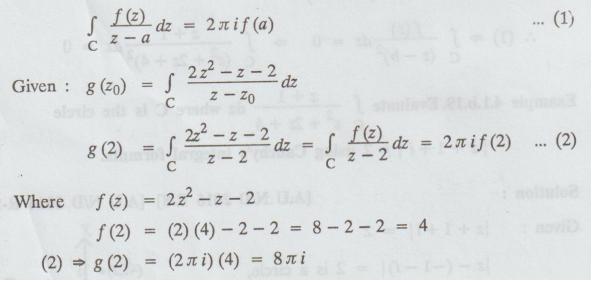
Probability and complex function: Unit IV: Complex integration : Tag: : Complex integration - Problems based on cauchy's integral formula
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
