Probability and complex function: Unit IV: Complex integration
Problems based on cauchy's integral theorem
Probability and complex function: Unit IV: Complex integration : problems based on cauchy's integral theorem
I. (a)
PROBLEMS BASED ON CAUCHY'S INTEGRAL THEOREM
Example 4.1.a.1. State
Cauchy's integral theorem. [Anna, May 1998] [A.U A/M 2015 R13, R8] [A.U April
2017 R-15 U.D]
Statement: If a function f(z) is analytic and its derivative f ' (z) is continuous at all points inside and on a simple closed curve C, then
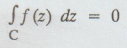
Example: 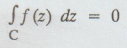 since sinz is an analytic function in C. [A.U A/M 2019 (R17)]
since sinz is an analytic function in C. [A.U A/M 2019 (R17)]
Example 4.1.a.2.
Evaluate 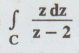 where C is the circle | z | = 1.
where C is the circle | z | = 1.
[A.U M/J 2014, N/D
2014]
Solution
: Let f (z) = z/z - 2
Here,
z= 2 lies outside C.
f(z)
is analytic inside and on C.
f
'(z)
is continuous inside C.
Hence,
by Cauchy's integral theorem 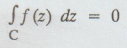
Example 4.1.a.3.
Evaluate 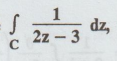 if C is the circle | z | = 1
if C is the circle | z | = 1
Solution :
Given: 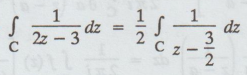
Let
f (z) = 1 / z – 3/2
Here,
z = 3/2 lies outside C
f(z)
is analytic inside and on C.
f
'(z)
is continuous inside C
Hence,
by Cauchy's integral theorem 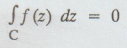
Example 4.1.a.4.
Evaluate 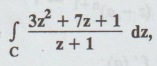 where C is | z | = ½ [A.U A/M 2018 R-17]
where C is | z | = ½ [A.U A/M 2018 R-17]
Solution:
Let f (z) = 3z2 + 7z + 1/z – (-1)
Here,
z= -1 lies outside C
Complex
Integration enpre
f(z)
is analytic inside and on C.
f'
(z) is continuous inside C.
Hence,
by Cauchy's integral theorem 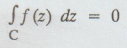
Example 4.1.a.5.
Evaluate 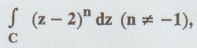 where C is | z-2 |= 4.
where C is | z-2 |= 4.
Solution: Let
f (z) = (2-2)n
f(z)
is analytic inside and on C.
By Cauchy's integral theorem, we get 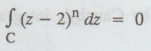
Example 4.1.a.6.
Evaluate 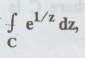 where C is | z | = 1. [Anna, Nov. 2001]
where C is | z | = 1. [Anna, Nov. 2001]
Solution:
Let f (z) = el/z
f(z)
is analytic inside and on C.
Hence,
by Cauchy's integral theorem we get 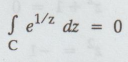
Example 4.1.a.7. Can the Cauchy-integral theorem be applied for evaluating the following integrals? Hence evaluate these integrals.
[A.U M/J 2016
R-8]
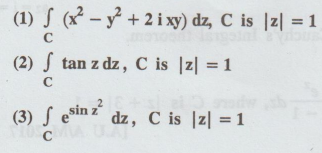
Solution:
(1) 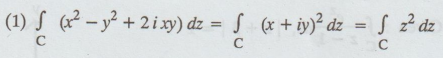
Let
f (z) = z2
f(z)
is analytic inside and on C. f' (z) is continuous inside C. Hence, by Cauchy's
integral theorem 
(2) 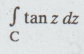
Let
f (z) = tanz = sin z / cos z is analytic except at z = ± π/2 , ±3π/2, ...
All
these points lie outside C. f'(z) is continuous inside C.
Hence,
by Cauchy's integral theorem 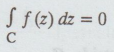
(3) 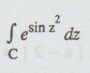
Let
f (z) = esinz2, f (z) is analytic inside and on C.
f'
(z) is continuous inside C.
Hence,
by Cauchy's integral theorem 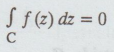
Example 4.1.a.8.
Evaluate 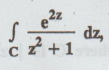 , where C is | z| = 1/2
, where C is | z| = 1/2
Solution:
Given: 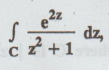
z2
+ 1 = 0
22
= -1
z
= ±i both lies outside C
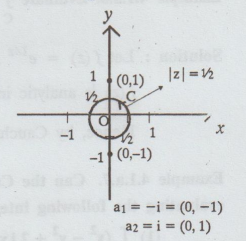
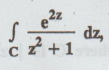 by Cauchy's Integral theorem.
by Cauchy's Integral theorem.
Example 4.1.a.9.
Evaluate 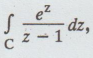 where C is | z + 3 | = 1 [A.U A/M 2017 R-08]
where C is | z + 3 | = 1 [A.U A/M 2017 R-08]
Solution: Given: 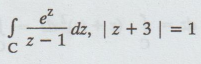
Here,
C is a circle with centre (-3, 0) radius 1.
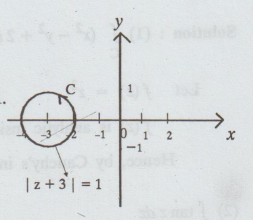
Let
f (z) = ez /z - 1
Here,
z= 1 lies outside C.
f
(z) is analytic inside and on C. f' (z) is continuous inside C.
Hence,
by Cauchy's integral theorem 
Example 4.1.a.10.
Evaluate 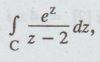 where C is the unit circle with centre as origin. [A.U
A/M 2017 R-13]
where C is the unit circle with centre as origin. [A.U
A/M 2017 R-13]
Solution:
Given: 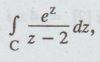
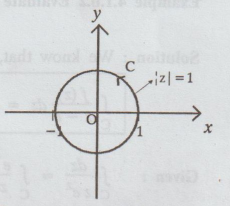
Here,
C is the unit circle with centre as origin.
Let
f (z) = ez/z - 2
Here,
z = 2 lies outside C
f
(z) is analytic inside and on C. f' (z) is continuous inside C.
Hence,
by Cauchy's integral theorem 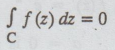
Example 4.1.a.11
Evaluate 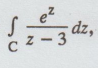 where C is the unit circle | z |= 1 [A.U April
2016 R-15 U.D]
where C is the unit circle | z |= 1 [A.U April
2016 R-15 U.D]
Solution:
Given: 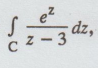
Here,
C is the unit circle with centre as origin.
Let
f (z) = ez/z - 3
Here,
z = 3 lies outside C
f(z)
is analytic inside and on C. f' (z) is continuous inside C.
Hence,
by Cauchy's integral theorem 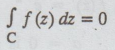
Probability and complex function: Unit IV: Complex integration : Tag: : - Problems based on cauchy's integral theorem
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
