Probability and complex function: Unit III: Analytic functions
Problems based on construction of analytic functions
Probability and complex function: Unit III: Analytic functions : Problems based on construction of analytic functions
PROBLEMS BASED ON CONSTRUCTION OF ANALYTIC FUNCTIONS
Example 3.3.1. Find a function w such that w = u + iv is analytic, if u = ex sin y. [Anna, May 2000]
Solution: Given: u = ex sin y
ux = ex sin y, ux (z, 0)= 0 [ sin 0 = 0]
uy = ex cos y, uy (z, 0) = ez [ cos 0 = 1]
Let w = f (z) = u + iv
f' (z) = ux + ivx
= ux - iuy [by C.R., condition]
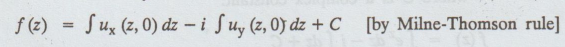
where C is a complex constant.
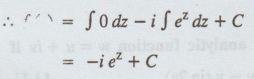
= - iez + C
Example 3.3.2 Construct the analytic function f (z) for which the real part is ex cos y [Anna, May 2001]
Solution: Given: u = ex cos y
ux = ex cos y, ux (z, 0) = ez [ cos 0 = 1]
uy = -ex siny, uy (z, 0) = 0 [ sin 0 = 0]
Let w = f(z) = u + iv
f' (z) = ux + ivx
= ux - iuy [by C.R., condition]
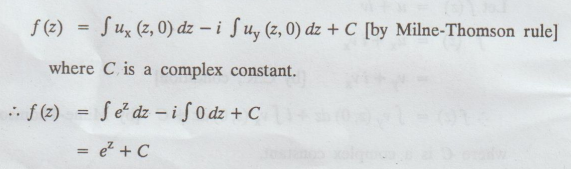
Example 3.3.3. Find the analytic function f (z) = u(x, y) + iv (x, y) whose real part is y + ex cosy. [Anna, May 1999]
Solution: Given:
u = y + ex cos y
ux = 0 + ex cosy, ux (z, 0) = ez
uy = 1- ex siny, Uy (z,0) = 1
Let w = f(z) = u + iv
f' (z) = ux + ivx
= ux - iuy [by C.R., condition]

Example 3.3.4 Determine the analytic function wu + iv if u = e2x (x cos 2y - y sin 2y). [A.U. A/M 2015 R13]
Solution: Given:
u = e2x (x cos 2y - y sin 2y)
ux = e2x [cos 2y] + (x cos 2y - y sin 2y) [2 e2x]
ux(z,0) = e2z [1] + [z (1) - 0] [2 e2z]
=e2z + 2z e2z
= (1 + 2z) e2z i.e., ux (z, 0) = (1 + 2z) e2z
uy = e2x [-2x sin 2y - (y 2 cos 2y + sin 2y)]
uy (z, 0) = e2z [- 0 - (0 + 0)] = 0 i.e., uy (z, 0) = 0
Let w = f(z) = u + iv
f’(z) = ux + ivx
= ux-i uy [by C.R., condition]
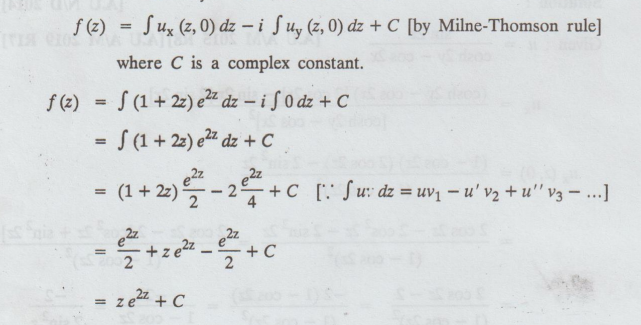
Example 3.3.5. Determine the analytic function where real part is u = x3-3xy2 + 3x2 - 3y2 + 1. [Anna, May 2001]
Solution :
Given: u = x3-3x2 + 3x2 - 3y2 + 1
uх = 3x2 - 3y2 + 6x, ux (z, 0) = 3z2 - 0 + 6z
uy = - 6xy + 0 - 6y, uy (z,0) = 0
Let w = f(z) = u + iv
f' (z) = ux + ivx
= ux - iuy [by C.R., condition]
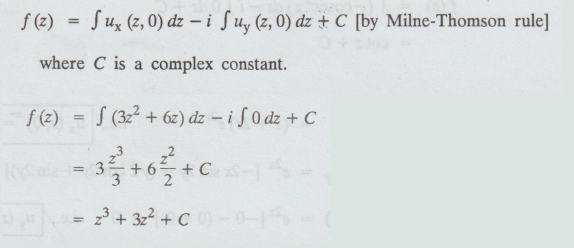
Example 3.3.6. (a) Determine the analytic function whose real part is sin 2x/ cosh 2y - cos 2x [Anna, May 1996] [A.U Tvli. A/M 2009] [A.U N/D 2012] [A.U N/D 2014] [A.U A/M 2015 R8] [A.U A/M 2019 R17]
Solution :
Given: u = sin 2x / cosh 2y - cos 2x
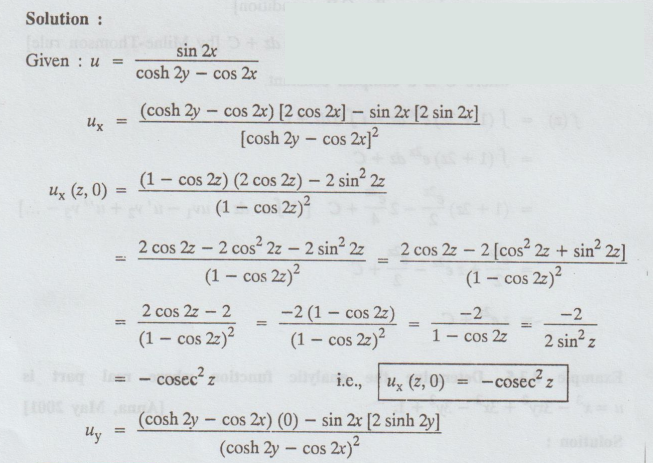
uy (z, 0) = 0
Let w = f(z) = u + iv
f' (z) = ux + ivx
= ux - iuy [by C.R. condition]
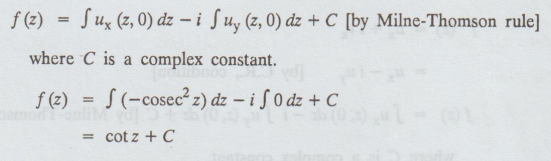
Example 3.3.6(b) Find an analytic function whose real part is ex (x cosy - y sin y) also find conjugate harmonic function. [A.U N/D 2016 R-13]
Solution:
u = ex (x cosy - y sin y)
ux = ex [cos y] + (x cosy - y sin y) [ex]
ux(z,0) = ez(1) + (z – 0)ez = ez + zez = (1 + z)ez
uy = ex [-x siny - (y cos y + sin y)]
uy(z,0) = ez [-0 - (0 + 0)] = 0
Let f(z) = u + iv
f' (z) = ux + ivx
= ux - iuy [by C.R., condition]
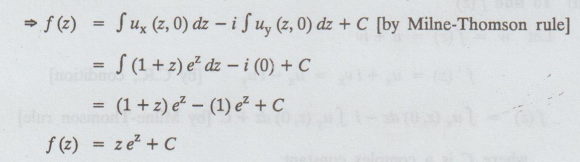
f(z) = zez + C
To find v :
u + iv = (x+iy) ex+iy + C
= (x + iy) ex eiy + C
→ u + iv = (x + iy) ex [cos y + i sin y]
= ex [x cosy - y sin y] + i ex [y cos y + x siny]
→ v = ex [y cos y + x sin y]
Example 3.3.7. Show that the function u = ½ log (x2 + y2) is harmonic and determine its conjugate. Also find f (z). [A.U A/M 2008, A.U A/M 2017 R8]
Solution :
Given:
u = ½ log (x2 + y2)
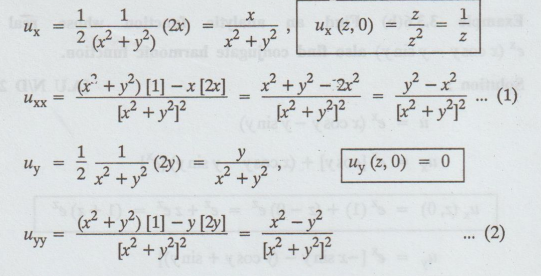
(i) To prove u is harmonic
uxx + uyy = (y2 - x2) + (x2 - y2) / (x2 + y2)2 = 0 by (1) & (2)
⇒ u is harmonic.
(ii) To find f (z)
Let w = f(z) = u + iv
f' (z) = ux + ivx = ux-i uy [by C.R., condition]
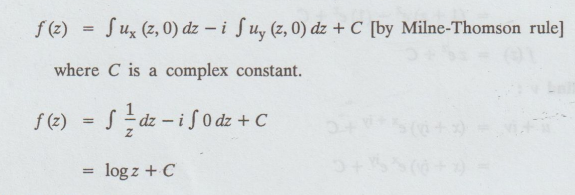
(iii) To find v :
f(z) = log (reiθ) [z = reiθ ]
u + iv = log r + log eiθ = log r + i θ
V = θ = tan -1(y/x)
Note: z = x + iy
r =|z| = √x2 + y2
logr = ½ log (x2+ y2)
tan θ = y/x
θ = tan-1 (y/x) i.e., v = tan-1 (y/x)
Example 3.3.8 Construct an analytic function f (z) = u + iv, given that novio u = ex2-y2 cos 2xy. Hence find v. [A.U D15/J16, R-08] [A.U A/M 2019, R-13]
Solution :

Example 3.3.9. Find the regular function whose imaginary part is e-x (x cos y + y sin y). [Anna, May 1996] [A.U M/J 2014]
Solution :
Given: v = e-x (x cos y + y sin y) nut olla nuo 8.8.
vx = e-x [cos y] + (x cos y + y sin y) [-e-x]
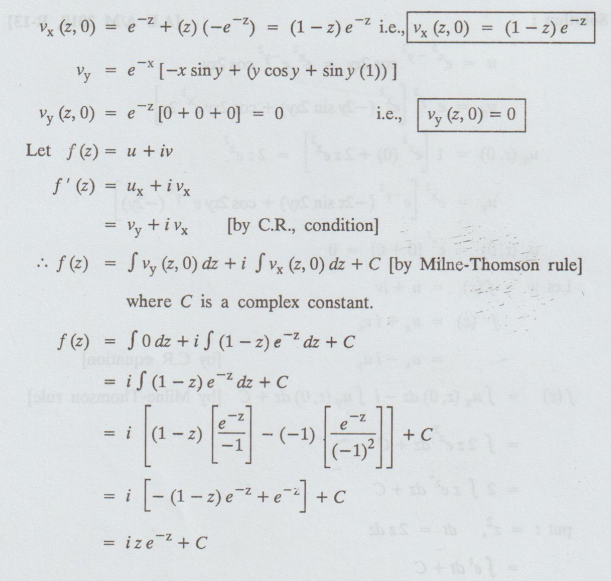
= i [-(1 - z) e-z + e-z ] + C
= ize-z + C
Example 3.3.10. In a two dimensional flow, the stream function is ψ = tan-1(y/x). Find the velocity potential p. [A.U M/J 2016 R13]
Solution :
Given : ψ = tan -1 (y/x)
We should denote, ϕ by u and ψ by v
V = tan -1 (y/x)
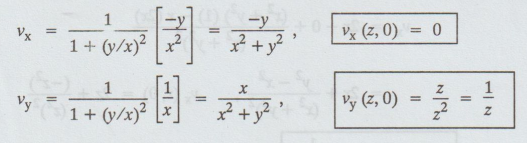
Let f (z) = u + iv
f' (z) = ux + i vx
= vy + ivx [by C.R., condition]
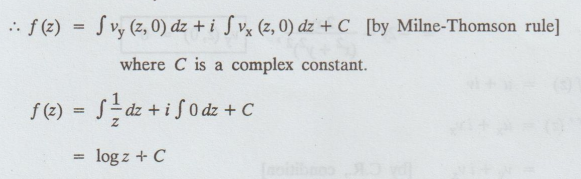
= log z + C
To find u :
f(z) = log (reiθ) [z = reiθ]
u + iv = log r + log eiθ
u + iv logr + iθ
u = log r
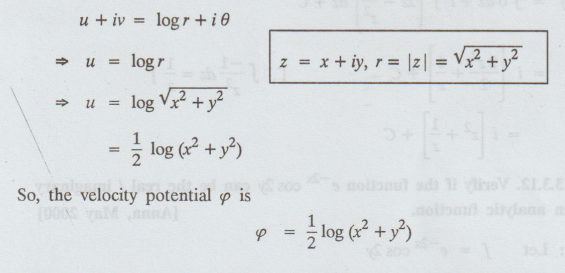
Note: In two dimensional steady state flows, the complex potential  is analytic.
is analytic.
Example 3.3.11. If w= u + iv is an analytic function and v = x2 – y2 + x / x2 + y2
find u. [Anna, May 1999]
Solution: Given: v = x2 - y2 + x/x2 + y2
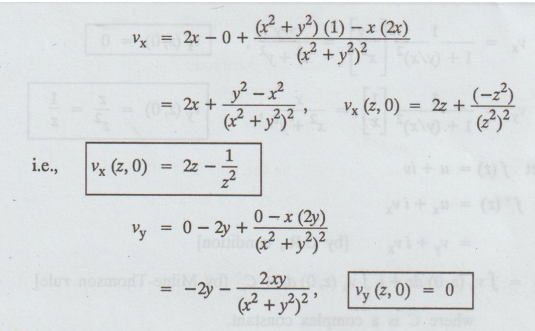
Let f (z) = u + iv
f' (z) = ux + ivx
= vy + i vx [by C.R., condition]
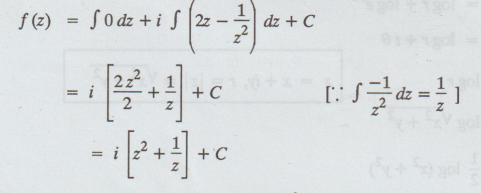
Example 3.3.12. Verify if the function e-2x cos 2y can be the real / imaginary part of an analytic function. [Anna, May 2000]
Solution: Let ƒ = e−2x cos 2y
fx = -2e-2x cos 2y
fxx = -4e-2x cos 2y
fy = -2e-2xsin 2y
fyy =-4e-2x cos 2y
fxx +fyy = 0 f is harmonic.
In a simply connected domain, every harmonic function is the real part or the imaginary part of some analytic function.
Therefore, Given is a real or imaginary part of an analytic function.
Example 3.3.13. Show that xy2 can not be the real part of an analytic function. (OR) Examine whether the function u = xy2 can be a real part of an analytic function. [A.U A/M 2018 R-17] [A.U CBT Dec. 2009]
Solution :
If a function is analytic its real part must be a harmonic function.
Let u = xy2
ux = y2 uy = 2xy
uxx = 0 uyy = 2
uxx + uyy = 2x ≠ 0 (except at x = 0 )
As u is not harmonic, it can not be the real part of an analytic function.
Example 3.3.14. Show that 2x (1 - y) can be the imaginary part of an analytic function.
Solution: In a simply connected domain, every harmonic function is the real part or imaginary part of some analytic function.
Let ν =2x (1 - y)
vx = 2 (1-y)
vxx = 0
vy = -2x
Vyy = 0
Thus vxx + vyy = 0.
Hence, v is harmonic and therefore it can be the imaginary part of an analytic function.
Example 3.3.15. If u and v are harmonic functions in a region R, prove that the function (uy - vx) + i (ux + vy) is an analytic function of z in R. [A.U Dec. 1997]
Solution: As u and v are harmonic, the following are true in R.
(i) uxx + uyy = 0
(ii) vxx + vyy = 0
(iii) Second order partial derivatives of u and v are continuous.
Let U = uy - vx and V = ux + Vy
Then Ux = uxy - vxx Vx = uxx + vxy
Uy = uyy - vxy vy = uyx + vyy
Ux = Vy if vxx + vyy = 0 which is true by (i)
Uy = -Vx if uxx + uyy = 0 which is true by (ii)
Further, Ux, Uy, Vx, Vy are continuous in R by (iii)
Hence, by sufficiency conditions of analyticity
U + iV is an analytic function of z.
Example 3.3.16. If f(z) = u+iv is an analytic function and u-v=ex (cos y sin y), find f (z) interms of z. (OR) Find the analytic function f(z) = u + iv if u – v = ex (cosy - sin y) [A.U Dec. 1997] [A.U A/M 2018 R-17]
Solution :
Given: u - v = ex (cos y - sin y) ....(A)
Differentiate (A) p.w.r. to x, we get
ux - vx = ex (cos y - sin y)
ux (z, 0) - vx (z, 0) = ez .....(1)
Differentiate (A) p.w.r. to y, we get
uy - vy = ex [- siny - cos y]
uy (z, 0) - vy (z, 0) = ez [-1]
i.e., uy (z, 0) - vy (z, 0) = - e-z
-vx (z, 0) - ux (z, 0) = -ez... (2) [by C.R. conditions]
(1) + (2) ⇒ −2vx (z, 0) = ez-ez = 0
=> vx (z, 0) = 0
(1) => ux(z,0) = ez
Let w = f(z) = u + iv
f'’(z) = u + iv
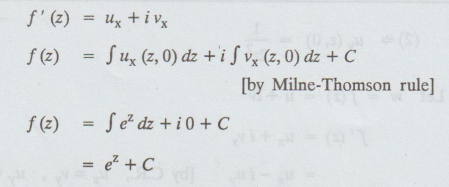
= ez + C
Example 3.3.17. Find the analytic function f(z) = u + iv if u + v = x/x2 + y2 and ƒ (1) = 1. IT-onliM
Solution: Given: u + v = x / x2 + y2
Differentiate (A) p.w.r. to x, we get
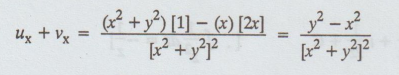
ux - uy = y2 – x2 / [x2 + y2]2 [ by C.R. condition]
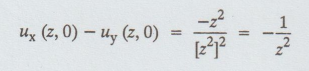
i.e., ux (z, 0) - uy (z, 0) = -1/z2 ....(1)
Differentiate (A) p.w.r. to y, we get
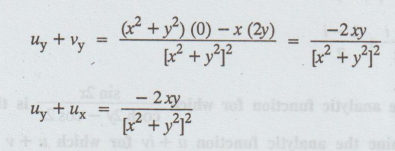
uy (z, 0) + ux (z, 0) = 0 ... (2)
(1) + (2) 2ux (z, 0) = -1/z2
ux (z, 0) = -1/ 2z2
(2) → uy (z,0) = 1/2z2
Let w = f(z) = u + iv
f' (z) = ux + ivx
= ux - i uy [by C.R., ux = vy, uy = -vx]
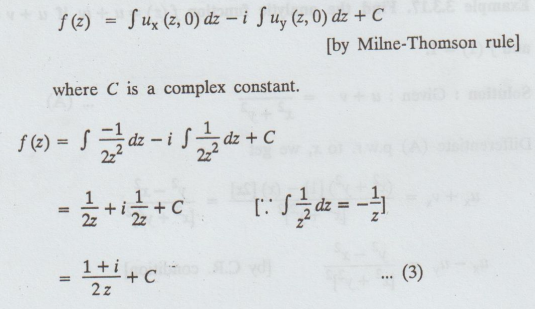
Given : f(1) =1
(3) ⇒f(1) = 1 + i / 2 + C = 1
⇒ C = 1 – ( 1 + i / 2) = 1 – i / 2
(3) ⇒ f(z) = 1 + i / 2z + 1 – i/ 2
Example 3.3.18. Find the analytic function for which sin 2x / cosh 2y - cos 2x is the real part. Hence determine the analytic function u + iv for which u + v is the above function. [A.U A/M 2019 (R17)] [Anna, May 2000, Anna, May 2001]
Solution :
Given: u + v = sin 2x / cosh 2y - cos 2x -...(A)
Differentiate (A) p.w.r. to x, we get
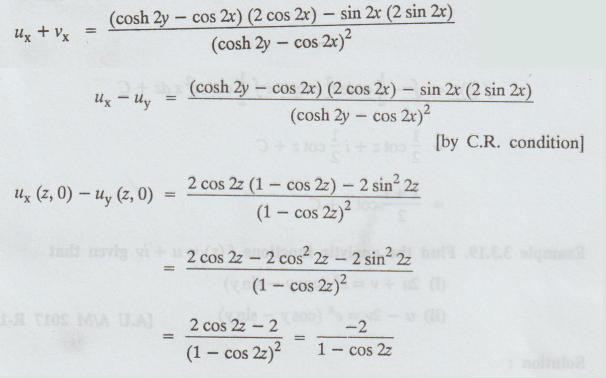
= 2 cos 2z – 2 / (1 – cos 2z)2 = -2/1-cos 2z
= -2/2 sin2z = -cosec2 z
ux (z, 0) - uy (z, 0) = -cosec2 z ....(1)
Differentiate (A) p.w.r. to y, we get
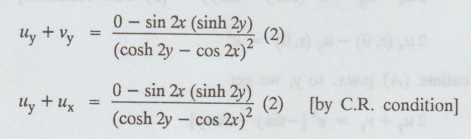
uy (z, 0) + ux (z, 0) = 0 .....(2)
(1) + (2) ⇒ 2ux (z, 0) = -cosec2 z
ux (z, 0) = - ½ csec2 z
(2) ⇒ uy(z,0) = ½ cosec2 z
Let w = f(z) = u + iv
f' (z) = ux + ivx
f’(z) = ux + ivx
= ux - iuy [by C.R., ux = vy, uy = -vx]
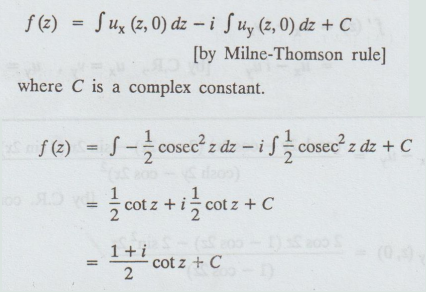
= ½ cot z + i ½ cot z + C
= 1 + i/2 cot z + C
Example 3.3.19. Find the analytic functions f (z) = u + iv given that
(i) 2u + v = ex (cos y - sin y)
(ii) u - 2v = ex (cos y - sin y) [A.U A/M 2017 R-13]
Solution :
Given: (i) 2u + v = ex (cos y - sin y) ....(A)
Differentiate (A) p.w.r. to x, we get
2ux + vx = ex (cos y - sin y)
2ux – uy = ex (cos y - sin y) [by C.R. condition]
2ux (z, 0) - uy (z, 0) = ez ....(1)
Differentiate (A) p.w.r. to y, we get
2uy + vy = ex [-siny - cos y]
2 uy + ux = ex [-siny - cos y] [by C.R. condition]
2 uy (z, 0) + ux (z, 0) = ez (-1) = -ez ....(2)
(1) × 2 ⇒ 4ux (z, 0) - 2 uy (z, 0) = 2 ez .....(3)
(2) + (3) ⇒ 5ux (z, 0) = ez
ux (z, 0) = 1/5 ez
(1) ⇒ uy(z,0) = 2/5 ez - ez = -3/5 ez i.e., uy (z, 0) = -3/5 ez
Let w = f(z) = u + iv
f' (z) = ux + ivx
= ux - iuy [by C.R., ux = vy, uy = -vx]
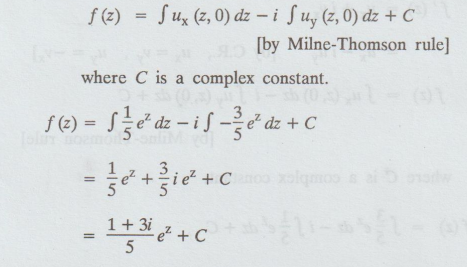
= 1 + 3i / 5 ez + C
(ii) u - 2v = ex (cos y - sin y) .....(A)
Differentiate (A) p.w.r. to x, we get
ux – 2vx = ex (cos y - sin y)
ux + 2 uy = ex (cos y sin y) [by C.R. condition]
vx (z, 0) + 2 uy (z, 0) = ez .....(1)
Differentiate (A) p.w.r. to y, we get
uy-2 vy = ex [-siny - cos y]
uy – 2 ux = ex [-siny - cos y] [by C.R. condition]
uy (z, 0) - 2ux (z,0) = -ez .....(2)

Example 3.3.20 Determine the analytic function f(z) = u + iv given that 3u + 2v = y2 - x2 + 16xy [A.U. N/D 2007]
Solution :
Given: 3u+2v = y2 - x2 + 16xy ...(A)
Differentiate (A) p.w.r. to x, we get
3 ux + 2vx = -2x+16y
3ux - 2uy = - 2x+16y [by C.R. condition]
3 ux (z, 0) - 2 uy (z, 0) = - 2z .....(1)
Differentiate (A) p.w.r. to y, we get

= z2 – i2z2 + C
= (1 – 2i)z2 + C
Example 3.3.21 Find an analytic function f(z) = u + iv, given that 2u + 3v = sin 2x / cosh 2y = cos 2x [A.U. A/M 2017 R-8]
Solution :
Given: 2u + 3v = sin 2x / cosh 2y = cos 2x ......(A)
Differentiate (A) p.w.r. to x, we get

Example 3.3.22 Find the analytic function f(z) = u + iv, given that 2u + 3y = ex (cos y - siny) [A.U A/M 2017 R-13]
Solution :
Given: 2u + 3y = ex (cosy - sin y)... (A)
Differentiate (A) p.w.r.to x, we get
2ux + 3vx = ex (cos y - siny)
2ux-3uy = ex (cos y - sin y) by C.R.
2ux (z, 0) - 3 uy (z, 0) = ez ....(1)
Differentiate (A) p.w.r.to y, we get
2uy + 3vy = ex[-siny - cos y]
2uy + 3ux = -ex [siny + cos y] by C.R
2uy (z, 0) + 3 ux (z, 0) = -ez ...........(2)
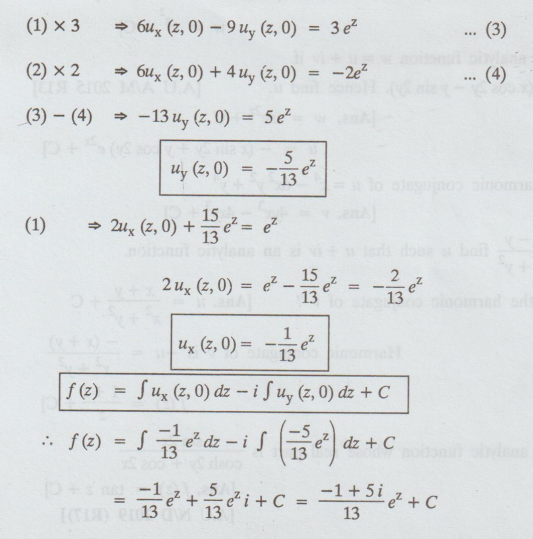
Probability and complex function: Unit III: Analytic functions : Tag: : - Problems based on construction of analytic functions
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
