Probability and complex function: Unit IV: Complex integration
Problems based on contour integration (Method 2)
Solved Example Problems
Probability and complex function: Unit IV: Complex integration : Problems based on contour integration
PROBLEMS BASED ON CONTOUR INTEGRATION
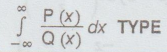
Example
4.4.2.
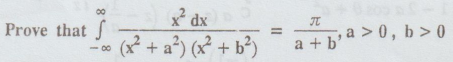
[Anna, May 2001] [A.U N/D 2007] [AU M/J 2009]
[A.U N/D 2005, N/D 2008, M/J 2013] [A.U A/M 2017 R-08] [A.U A/M 2019 R-13] [A.U
A/M 2019 R-8]
Solution
:
Conside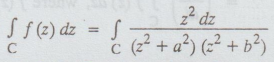r 
where C is the upper half of the semi-circle r with the
bounding diameter [-R, R].
Example
4.4.5(a)
Solution:
See
Example 4.4.5
Example
4.4.6(a) Evaluate
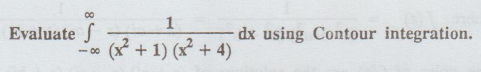
Solution
:
See
Example 4.4.6
Example 4.4.8
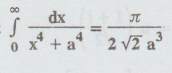
Solution:
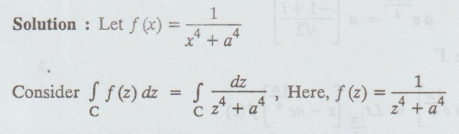
where
C is the upper half of the semi-circle I with the bounding diameter [-R, R]
Type
III
TYPE
4
Integrals
of the type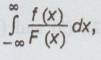 
where F(x) has zeros on the real axis.
The
singularities on the real axis are enclosed in small semi-circle to avoid their
inclusions in C, i.e., the contour C is indented at these singularities.
IX.
Problems based on integrals of the type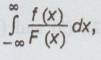
where F(x) has zeros on the real axis.
Example
4.4.12. Show that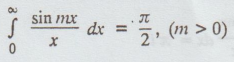 
Solution :
Probability and complex function: Unit IV: Complex integration : Tag: : Solved Example Problems - Problems based on contour integration (Method 2)
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation