Problems based on contour integration

Problems based on contour integration

 

Example 4.4.1.

 

Example 4.4.1(a)

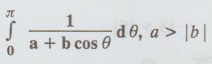
Solution :

 

Example 4.4.1(b)

 [A.U May 1999, Nov. 2001] [A.U. A/M 2008] [A.U. N/D 2008, 2009, 2010] [A.U. M/J 2010, A/M 2011] [A.U M/J 2016 R-8]

Solution:

 

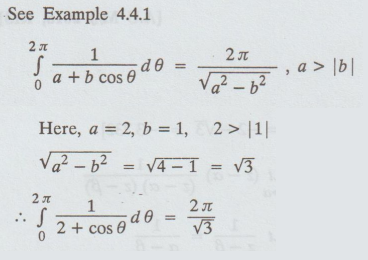
Example 4.4.1 (c) Using Contour integration, evaluate

Solution :

See Example 4.4.1

 

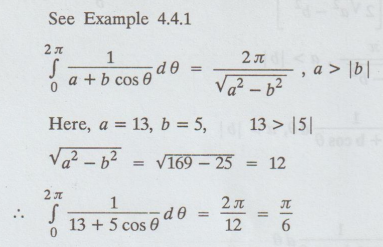
Example 4.4.1(d)

Solution :

See Example 4.4.1

 

Example 4.4.1(e)  by using contour integration.

Solution :

See Example 4.4.1

 

Example 4.4.2

Solution :

 

Example 4.4.2 (a)

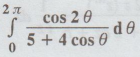
Solution :

See Example 4.4.2

Example 4.4.2 (b) Show that 

Solution :

See Example 4.4.2.

 

Example 4.4.2(c) Show that 

 [A.U M/J 2013, A/M 2015 R8, N/D 2015 R13]

[2003 QV U.A]

Solution :

See Example 4.4.2

 

Example 4.4.2 (d)

Solution :

 

Example 4.4.2 (e) Using the Contour integration, evaluate the real integral

 [A.U N/D 2005]

Solution :

 

Examle 4.4.3

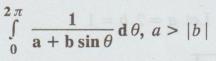
Solution :

 

Example 4.4.3 (a) Using Contour integration, Evaluate 

 [A.U May 1998, A.U Nov. 1996, A.J M/J 2008, M/J 2014]

 [A.U N/D 2019 R-17] [A.U A/M 2019 R-17]

Solution :

See Example 4.4.3

 

Example 4.4.3 (b)

 [A.U M/J 2007]

Solution :

(1) See Example 4.4.3

 

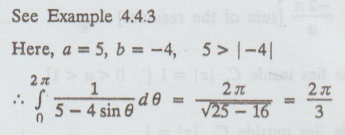
Eample 4.4.4

Solution :

Type II.

Improper integrals of the form  where P (x) and Q (x) are polynomials in x such that the degree of Q exceeds that of P at least by two and Q (x) does not vanish for any x.