Example Solved Problems based on Properties harmonic conjugates

PROBLEMS BASED ON PROPERTIES

B.W.(1) If f (z) = u + iv is a regular function of z in a domain D, then 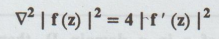 A.U May 1997, Dec. 1997, Nov. 2001, Nov. 96, A/M 2008, May 2001, M/J 2012, N/D 2014, M/J 2016 R-8, M/J 2016 R-13, A/M 2017 R-08, April 2016 R-15 U.D, April 2017 R-15 U.D

Solution: Given: f(z) = u + iv

Note : f (z) = u + iv; f' (z) = u_x + iv_x;

(or)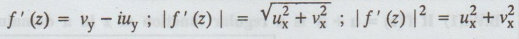 

B.W. (2) If f(z) = u+ iv is a regular function of z in a domain D, then  log |f(z) | = 0 if f (z) f' (z) ≠ 0 in D. i.e., log | f (z) | is harmonic in D. [A.U A/M 2017 R-13] [A.U A/M 2019 R-08]

Solution: Given: f(z) = u + iv

|f(z) | = √u² + y²

B.W. (3) If f(z) = u+ iv is a regular function of z in a domain D, then 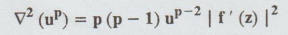  [A.U A/M 2018 R-17]

Solution:

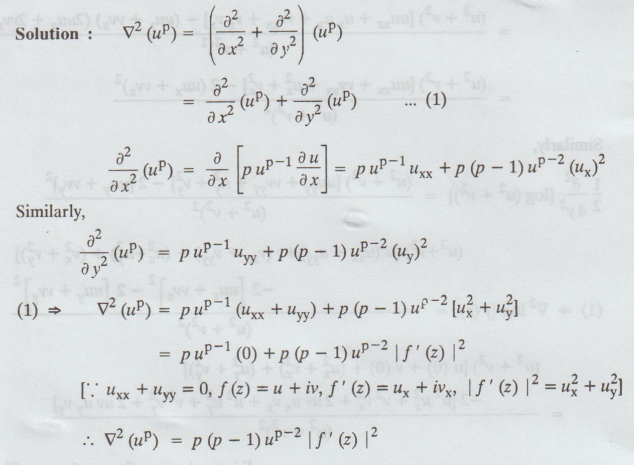
B.W. (4). If f (z) = u + iv is a regular function of z, then 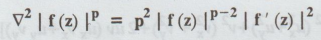 [A.U N/D 2015 R-13]

 Solution : f(z) = u + iv

|f(z) | = √u² + y² ......(a)

|ƒ (z) |^p = (u² + v²)^p/2 ......(b)

B.W. (5) If f (z) = u + iv is a regular function of z, then  [arg f (z)] = 0, i.e., arg f(z) is harmonic in D.

Solution :

arg f(z) = tan ^-1(v/u)

B.W. (6) If f (z) = u + iv is a regular function of z in a domain D, then 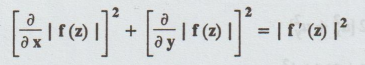  [A.U A/M 2015 R8]

Solution : Given: f(z) = u + iv

|f(z) | = √u² + i²

∂/∂x |f(z) | = ∂ /∂ x [√u² + v² ]

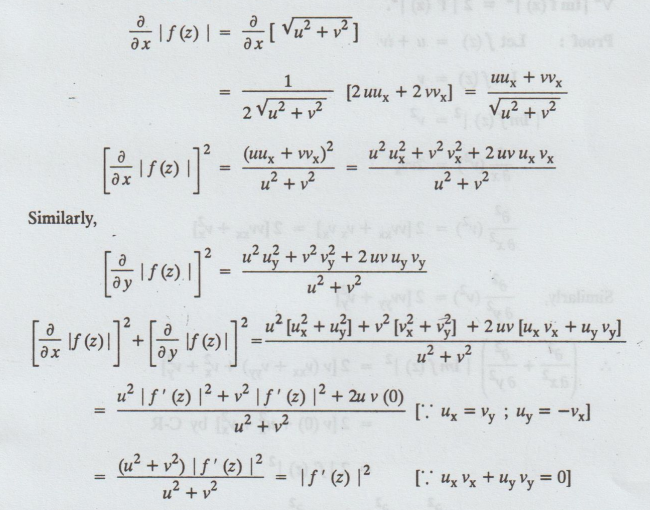
B.W. (7) If f (z) = u + iv is a regular function of z, then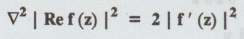

Solution :

 f(z) = u + iv

Re f(z) = u

| Ref (z) |² = u²

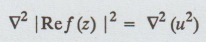
= ( ∂²/∂x² + ∂²/∂y²) (u²)

= ∂²/∂x²(u²) + ∂²/∂y²(u²) .....(1)

See Book Work 1. Page No. 3.29

= 2[ u²_x + u²_y ]

= 2 f'| (z) |²

B.W. (8) If f(z) = u + iv is a regular function of z, then prove that 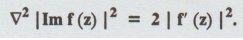| Im f (z) |²  = 2 | f' (z) |².

Proof :

Let f (z) = u + iv

Imf(z) = v

| Im f (z) |² = v²

∂/∂x (v²) = 2vv_x

∂²/∂x² (v²) = 2 [ vv_xx + v_xv_x ] = 2 [ vv_xx + v²_x ]

Similarly, ∂²/∂y² = 2 [vv_yy + v²_y ]

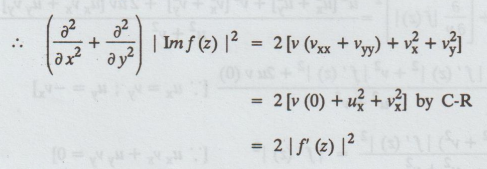
B.W. (9) Show that ∂²/∂x² + ∂²/∂y² = 4 ∂²/∂z∂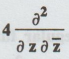 

Proof: Let f be a function of x and y

where x & y are functions of z and 

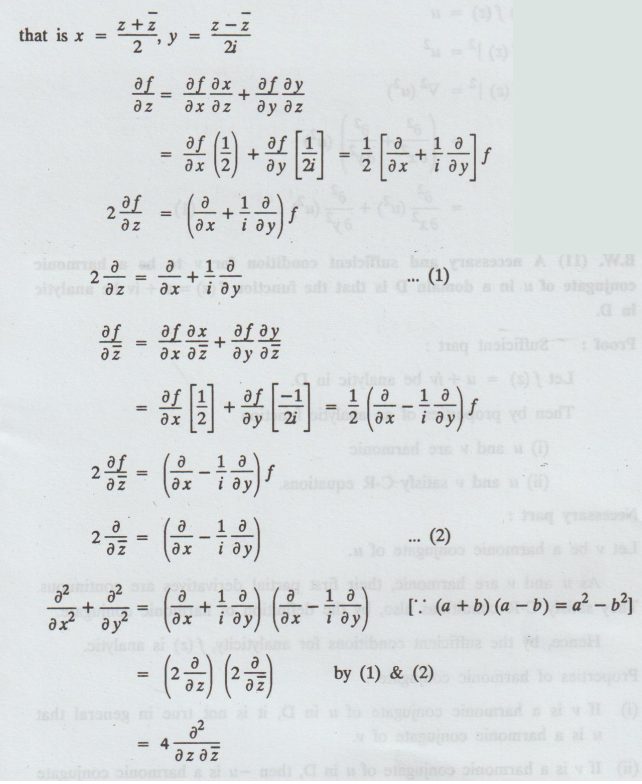
B.W. (10) If f (z) is analytic, show that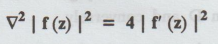  

Solution: Second method: See first method in Page No. 3.29

We know that,

B.W. (11) A necessary and sufficient condition for v to be a harmonic conjugate of u in a domain D is that the function f(z) = u + iv be analytic in D.

Proof : Sufficient part :

Let f (z) = u + iv be analytic in D.

Then by properties of an analytic function

(i) u and v are harmonic

(ii) u and v satisfy C-R equations.

Necessary part :

Let v be a harmonic conjugate of u.

As u and v are harmonic, their first partial derivatives are continuous. They satisfy C-R conditions also, by the definition of harmonic conjugate.

Hence, by the sufficient conditions for analyticity, f (z) is analytic.

Properties of harmonic conjugate :

(i) If v is a harmonic conjugate of u in D, it is not true in general that u is a harmonic conjugate of v.

(ii) If v is a harmonic conjugate of u in D, then -u is a harmonic conjugate of v in D and conversely.

(iii) If u and v are to be harmonic conjugates of each other, then both u and v must be constant functions.

(iv) If u is a harmonic function in a simply connected domain D, then it has a harmonic conjugate there.

(v) A harmonic conjugate when it exists, is unique except for an additive constant.