Problems based on Taylor's and laurent's series

PROBLEMS BASED ON TAYLOR'S SERIES

 

I. TAYLOR'S SERIES ABOUT z = 0 PROBLEMS

Example 4.2.1. Expand e^z in a Taylor's series about z = 0

Solution :

 

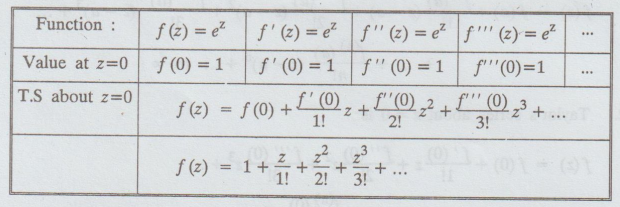
Example 4.2.2. Expand f (z) = log (1 + z) as a Taylor's series about z = 0 if | z | < 1

[AU N/D 2006]

Solution :

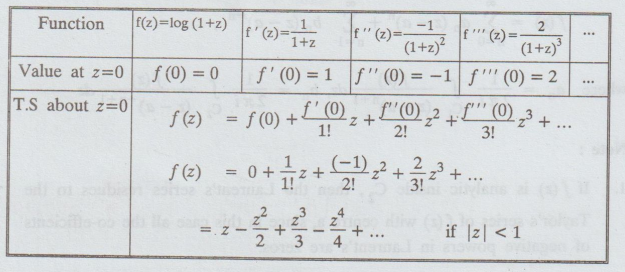
II. TAYLOR SERIES ABOUT z = a PROBLEMS

Example 4.2.3. Expand 1 / z – 2 at z = 1 in a Taylor's series  [AU N/D 2005]

Solution :

 

Example 4.2.4. Find the Taylor's series for 1/z about (i) z = 1, (ii) z = 2,  (iii) z = i

Solution :

 

Example 4.2.5. Expand f (z) = 1/x² as a Taylor series about the point z = 2

[A.U M/J 2016 R-13]

 

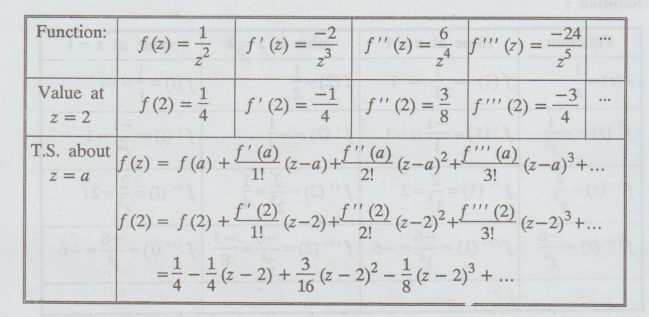
Example 4.2.6. Expand f (z) = cos z about z = π / 3 in Taylor's series.

Solution :

Note: In some cases, Taylor's theorem itself can be used to obtain Taylor's series.

This is the case when nth derivative of the given function is known explicitly.

Some important formulae

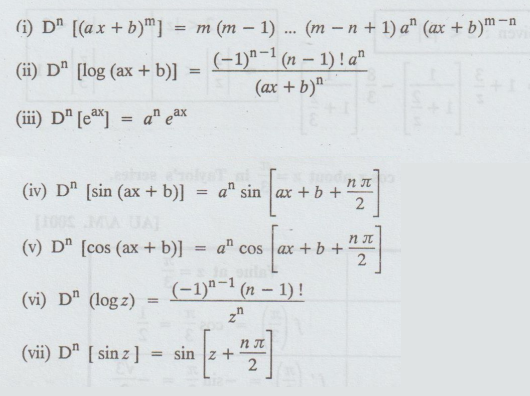
III. PROBLEMS BASED ON LAURENT'S SERIES

Example 4.2.7. Find the Laurent's series of f (z) = z² – 1 /  z² + 5z + 6 valid in the region (i) 2 < | z | < 3 (ii) | z❘ <2 (iii) | z |  >3

[A.U N/D 2004, M/J 2009, A/M 2011, N/D 2011] [A.U M/J 2013, M/J 2014] [A.U A/M 2015 R13] [A.U N/D 2019 R17], [A.U A/M 2019 R17]

Solution:

Example 4.2.8. Find the Laurent's series expansion of the function

z – 1 / (z + 2) (z+3)' valid in the region 2< | z | < 3. [Anna, Nov., 2001]

[A.U M/J 2006]

Solution :

Example 4.2.9. Evaluate f (z) = 1 / (z+1) (z+3) in Laurent's series valid for the regions | z | > 3 and 1 <  | z | < 3

 [A.U N/D 2009, M/J 2012]

Solution:

 

Example 4.2.10. Expand f (z) = 1 / z (z - 1) as Laurent's series in powers of z and state the respective region of validity.

[A.U N/D 2007, J/J 2008]

Solution:

Given: f (z) 1 / z (z - 1)

f(z) is not analytic at z = 0 and z = 1

Now, the function f (z) is not analytic at z = 0 and

z = 1 but it is analytic in the regions.

1. 0 < z < 1 (Deleted disc)

2. | z | > 1

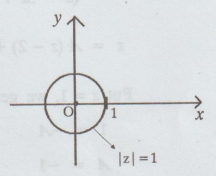
Case (i) For all z in the deleted disc 0 < | z | < 1 that is in the disc | z | < 1 from which z = 0 is deleted. So in this annulus, we have

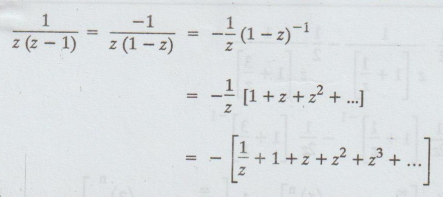
The region of validity of this expansion is 0 < |z| < 1

Case (ii) In the region | z | > 1

we have | 1/z | < 1

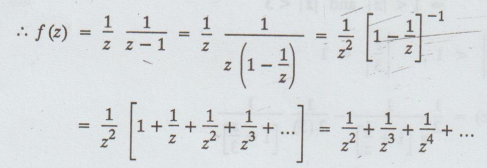
The region of validity of this expansion is | z | > 1.

 

Example 4.2.11 Expand as a Laurent's series the function

f(z) = z / (z² - 3z + 2) in the region

(i) | z | < 1, (ii) 1 < |z| < 2, (iii) z > 2, (iv) |z – 1| < 1 [A.U. M/J 2016 R-13] [A.U N/D 2015 R-13]basqa

Solution :

 

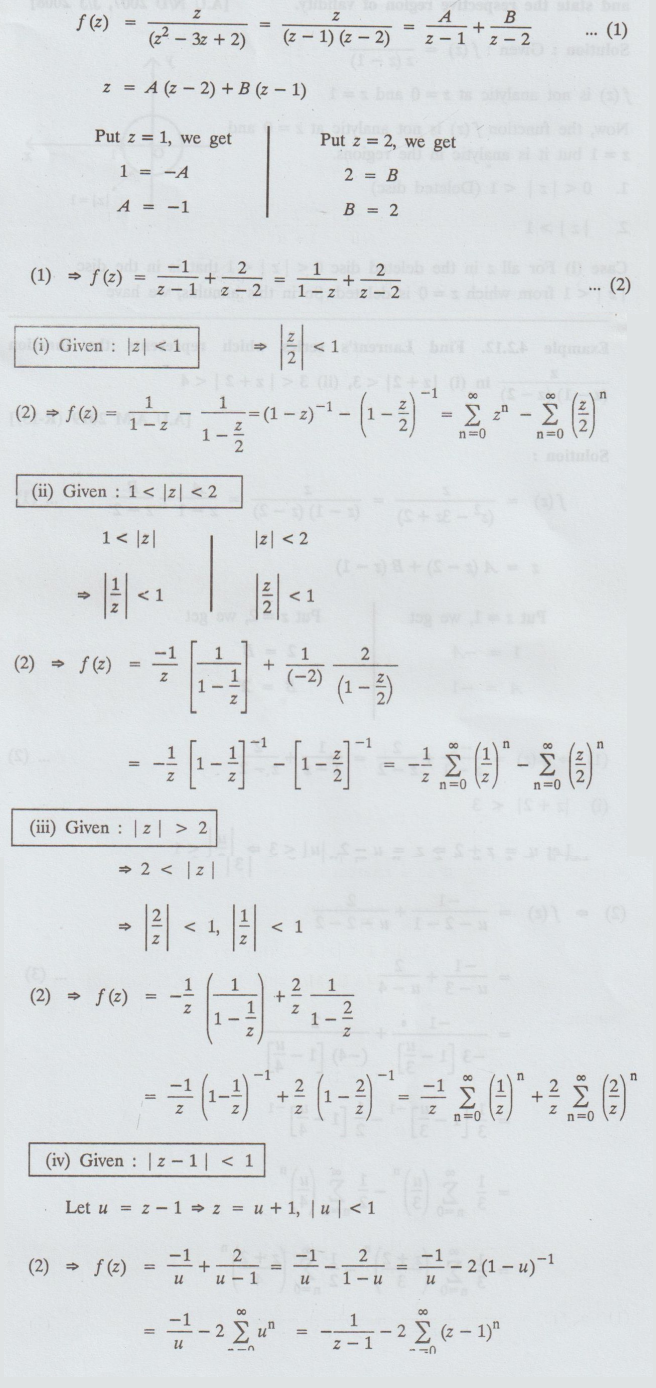
Example 4.2.12. Find Laurent's series which represents the function

z / (z - 1) (z - 2) in (i) |z + 2| < 3, (ii) 3< | z + 2 | < 4

[A.U A/M 2019 (R-13)]

Solution :

 

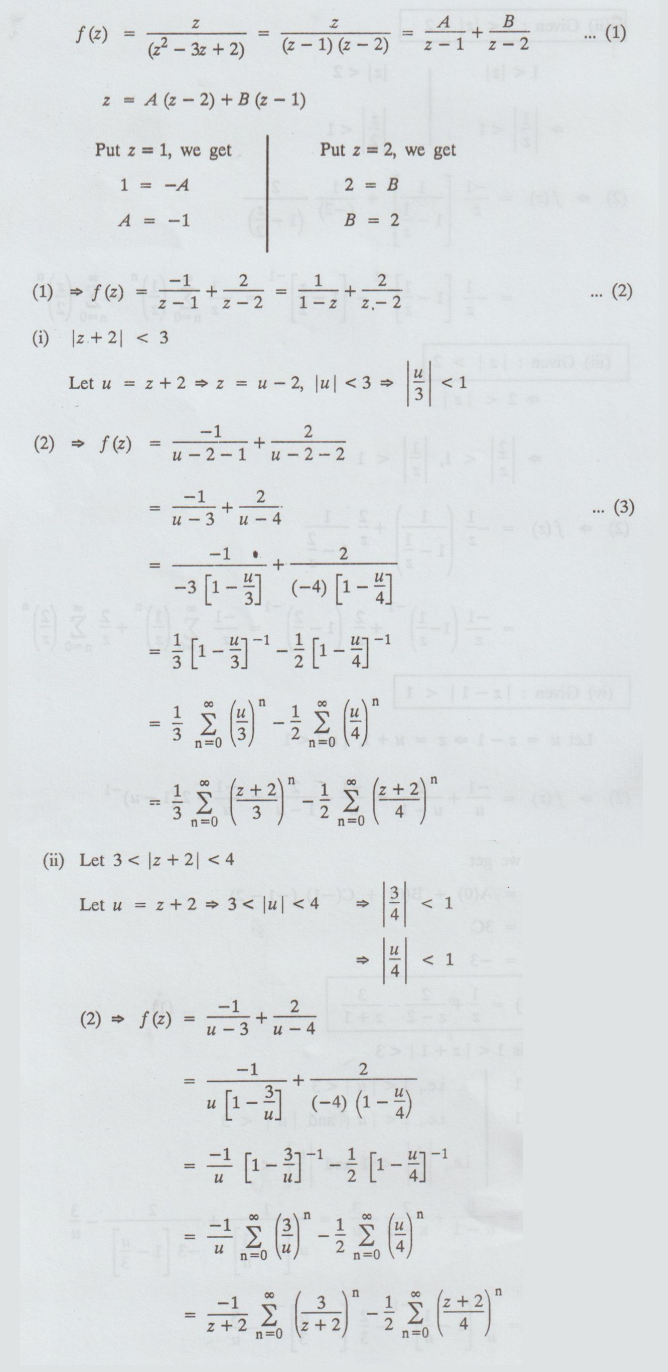
Example 4.2.13 Find the Laurent's expansion of

f(z) = 7z – 2 / z (z - 2) (z + 1) valid in 1 < |z + 1| < 3

[Anna, Nov. 1996]

[A.U M/J 2010, CBT M/J 2008] [A.U J/F 20909, N/D 2010] [A.U D15/J16 R-08, A.U April 2016 R-15 U.D] [A.U A/M 2015 R8]

Solution :

 

Example 4.2.14. Obtain Laurent's expansion for f(z) = 1 / (z-1) (z - 2) Valid in the regions. (i)|z - 1| < 1 (ii) 1 < | z | < 2 (iii) | z | > 2

 [Anna, May 2002] [A.U N/D 2014 R-13]

Solution :

Note : z = 0 is an essential singularity.

 

Example 4.2.15. Find the residues of f (z) = z² / (z − 1) ² (z + 2)² at its isolated singularities using Laurent's series expansions. Also state the valid region.

[A.U. N/D 2006, M/J 2007, N/D 2010, N/D 2012]

Solution:

Both z = 1, z = -2 are isolated singularities of f (z)

To find the residue of f (z) at z = 1,

we have, f (z) in series of powers of (z - 1), valid in 0 < |z-1|  <r

To find the residue of f (z) at z = -2, we have to expand f (z) in series of powers of (z+2), valid is 0 < | z + 2 |< r

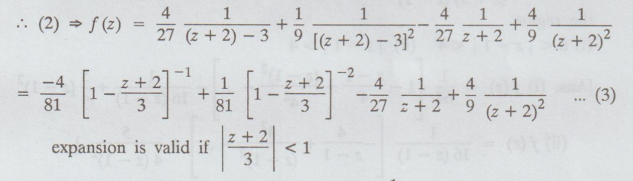
 [Residue of f (z) at z = 2] = Co-efficient of 1 / z + 2  in (3) used

= - 4 / 27

The validity of the region is 0 < |z + 2 | < 3