Probability and complex function: Unit II: Two dimensional random variables
Problems under continuous random variables
Two dimensional random variables
Probability and complex function: Unit II: Two dimensional random variables : Problems under continuous random variables
PROBLEMS UNDER CONTINUOUS RANDOM VARIABLES
Example
2.1.9
Suppose
the point Probability Density Function (PDF) is given by
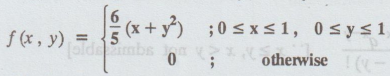
Obtain
the marginal PDF of X and that of Y. Hence, otherwise find P [1/4 ≤ y ≤ 3/4]
Solution:

Example
2.1.10
Let
X and Y have j.p.d.f f(x, y) = 2, 0 < x < y < 1. Find the m.d.f. and
the conditional density function of Y given X = x. [A.U. A/M 2003] [A.U CBT A/M 2011]
Solution:
The
marginal density function of X is given by

Example
2.1.11
The
joint probability density function of a random variable X and Y is given by,
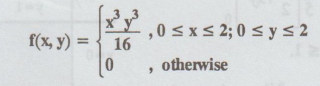
Find
the marginal densities of X and Y.
Also,
prove that X and Y are independent.
Solution:
The
marginal density of X is given by,
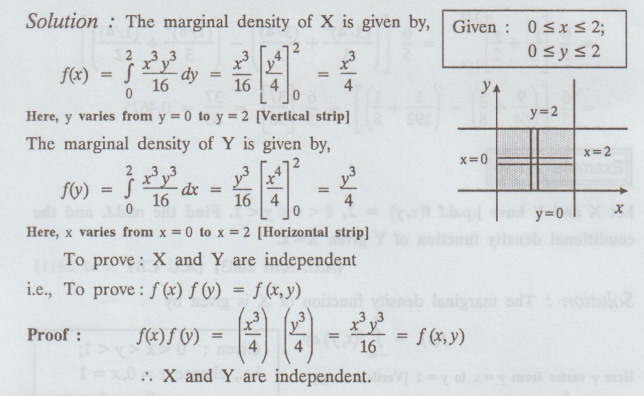
Example
2.1.12
The
joint p.d.f of the random variable (X, Y) is given by f(x, y) = Kxy e-(x2
+ y2), x > 0, y > 0. Find the value of K and also prove that X and
Y are independent.
[A.U. May, 2000, 2004, N/D 2006, N/D 2011, M/J
2012] [N/D 2007, M/J 2009, Tvli A/M 2009, N/D 2013] [A.U A/M 2015 (RP) R13, R8]
[A.U N/D 2018 R-13 RP]
Solution:
Here,
the range space is the entire first quadrant of the xy-plane.

Example
2.1.13
Given
fxy (x, y) = Cx (x − y), 0 < x < 2, -x < y < x and 0, elsewhere
(a) Evaluate C; (b) Find fx(x); (c)
fy/x (y/x). and (d) fy (y)
[A.U.
N/D 2004, M/J 2006, N/D 2010, M/J 2013] [A.U N/D 2016 R13 (PQT, RP)]
Solution
: By the property of j.p.d.f, we have,
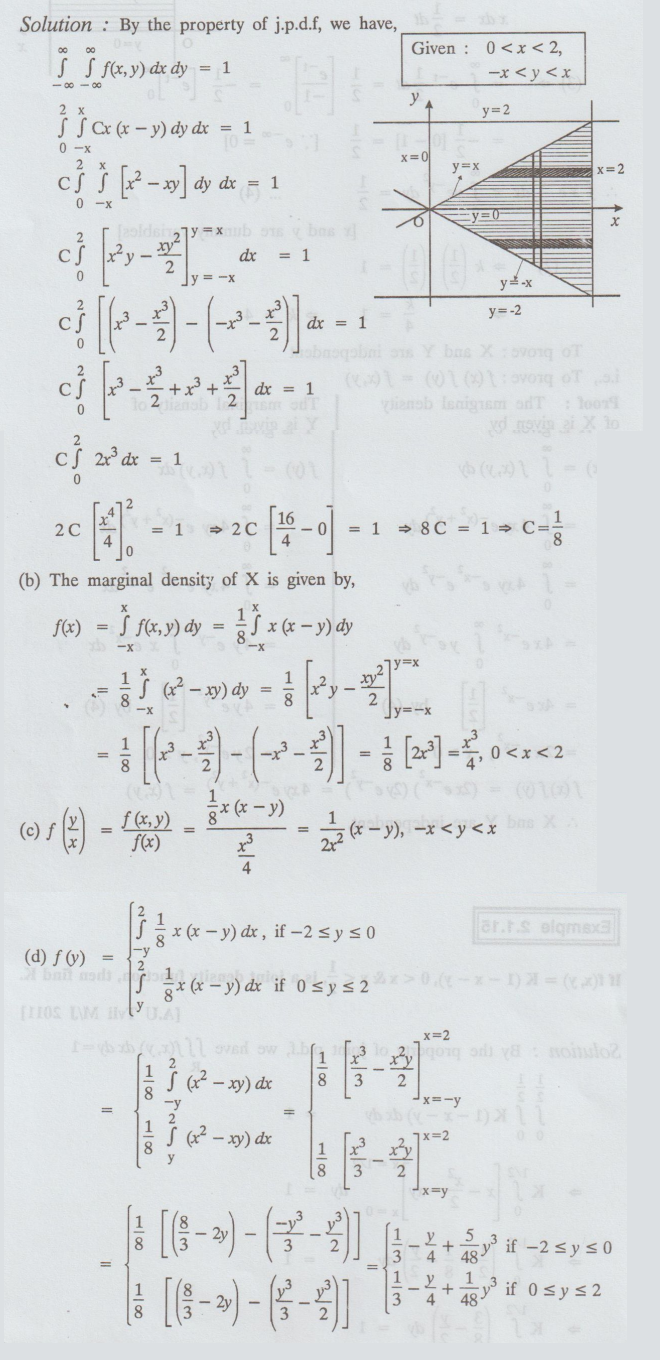
Example
2.1.14
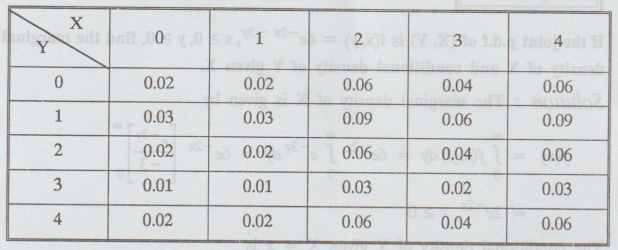
Suppose
that X and Y are independent and that these are the distribution tables for X
and Y.

What
is the joint probability space?
Solution:
Since, X and Y are independent,
f(x,
y) = f(x). f(y), ∀ (x,y)
Hence,
the joint probability space is given by,
Example
2.1.15
If
f(x, y) = K (1 − x − y), 0 < x & y < 1/2, is a joint density
function, then find K. [A.U Tvli M/J 2011]
Solution:
By the property of joint p.d.f, we have 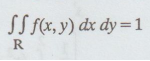
Example 2.1.16
If
the joint p.d.f of (X, Y) is f(x, y) = 6e-2x-3y, x = 0, y ≥ 0, find
the marginal density of X and conditional density of Y given X.
Solution:
The marginal density of X is given by
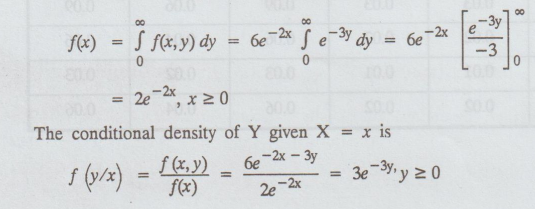
Example
2.1.17
The
j.p.d.f of (X, Y) is given by f(x,y) = e−(x + y), 0 ≤ x, y < ∞.
Are
X and Y independent? Why?
[A.U.
A/M.2008] [A.U Tvli M/J 2010, Trichy M/J 2011, N/D 2011] [A.U N/D 2015 R13 RP]
[A.U A/M 2017 R-13]
Solution:
Given:
f (x, y) = e-(x + y), 0 ≤ x,
y < ∞
To
prove: X and Y are independent.
i.e.,
To Prove: f (x)f (v) = f(x, y)

Hence,
X and Y are independent.
Example
2.1.18
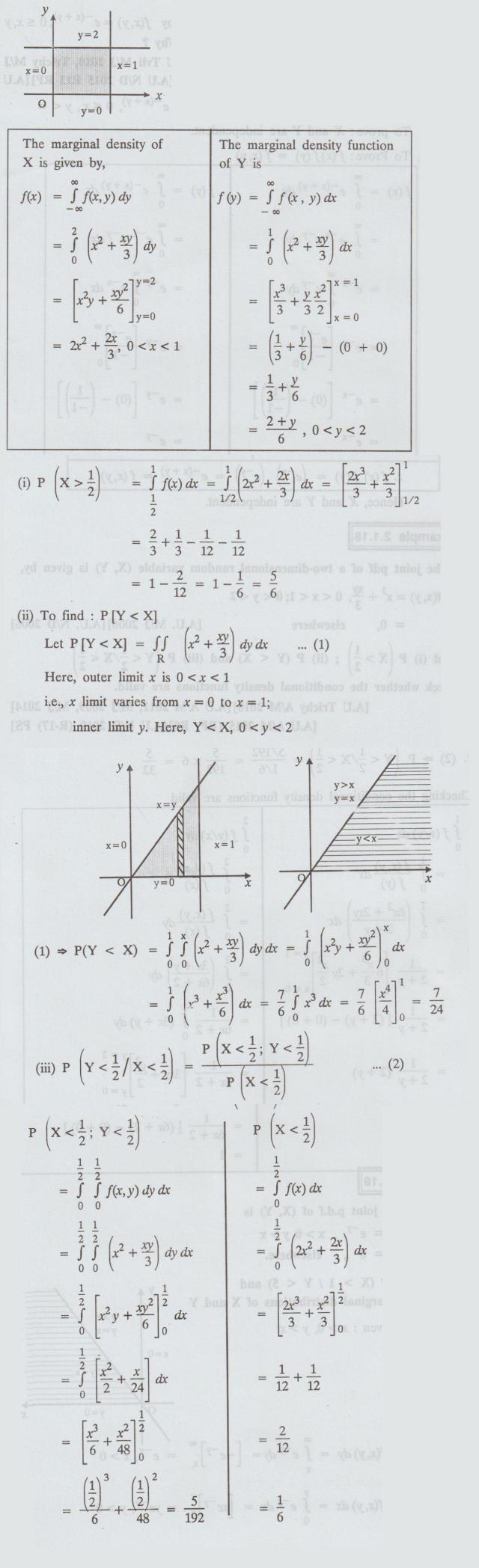
If
the joint pdf of a two-dimensional random variable (X, Y) is given by,
f(x,y)
= x2 + xy/3, 0 < x < 1;0 < y < 2
=
0 , elsewhere
Find (i) P(X > 1/2) ; (ii) P(Y < X) and (iii) P (Y < 1/2 / X < 1/2)
Check
whether the conditional density functions are valid.
[A.U
Trichy A/M 2010] [A.U A/M 2011, M/J 2009, M/J 2014]
[A.U
A/M 2015 (RP) R8] [A.U N/D 2019 (R-17) PS]
Solution:
Given: 0 < x < 1, 0 < y < 2

Example
2.1.19
Given
that the joint p.d.f of (X, Y) is
f(x,
y) = e-y, x > 0, y > x
=
0, elsewhere.
Find
(i) P (X > 1/Y < 5) and
(ii)
the marginal distributions of X and Y
Solution:
Given: x > 0, y > x

Example
2.1.20
The
joint density function of the RVS X and Y is given by,
f(x,
y) = 8xy, 0 < x < 1; 0 < y < x
=
0, elsewhere
[A.U
Trichy A/M 2010]
Find
P(Y < 1/8/ X < 1/2). Also find the conditional density function of
[AU,
May 1999, N/D 2005, N/D 2009]
Solution
:
The
marginal density function of X is given by,

Example
2.1.21
If
the joint p.d.f of (X, Y) is given by f(x, y) = K, 0 ≤x≤ y ≤2 find K and also
the marginal and conditional density functions.
Solution
:
By
the property of joint p.d.f we have

Example
2.1.22
If
the joint density function of the two random variables 'X' and 'Y' be
f(x,
y) = e-(x + y), x ≥ 0, y ≥ 0
=
0, otherwise
[A.U N/D. 2003]
Find
(i) P(X < 1) and (ii) P(X + Y < 1)
[A.U N/D. 2009] [A.U CBT M/J 2010] [A.U N/D
2019 (R17) PQT]
Solution
:
To find the marginal density function of X.
Let
the marginal density function of X be g (x) and it is defined as

Example
2.1.23
The
joint p.d.f of the random variables X and Y is given by
P(x,
y) = xe -x (y+1) where 0 ≤ x, y < ∞. (i) Find P(x) and P(y) and
(ii)
Are the random variables independent ?
Solution:
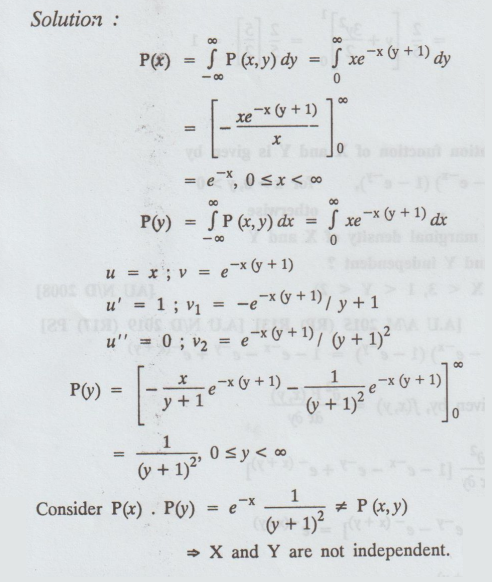
Example
2.1.24
S.T.
the function
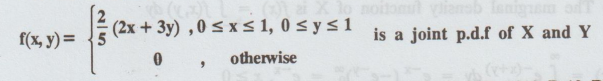
Solution :
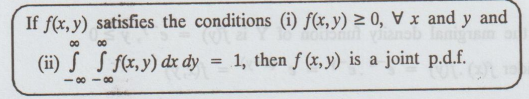
(i)
f(x, y) ≥ 0 in the given interval, 0 ≤ x, y ≤ 1
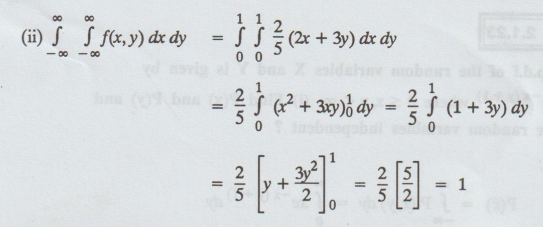
Example
2.1.25
If
the joint distribution function of X and Y is given by
F(x,
y) = (1 – e-x) (1 − e-y),
for
x > 0, y > 0
otherwise
(i)
Find the marginal density of X and Y
(ii)
Are X and Y independent ?
(iii)
P(1 < X < 3, 1 < Y < 2)
Solution:

Example
2.1.26
The
joint density function of two random variables X and Y is

Example
2.1.29

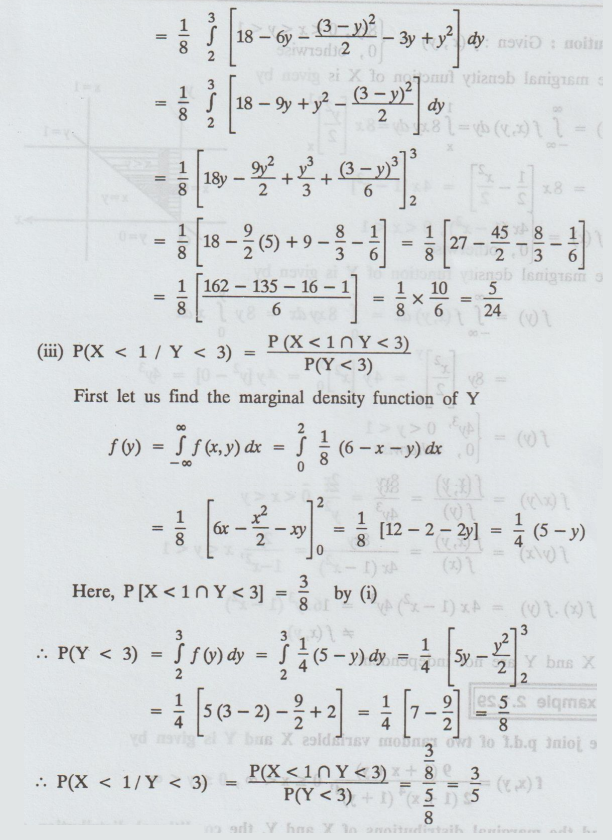
Example
2.1.28
Given
the joint p.d.f of (X, Y) as of
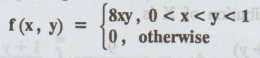
Find
the marginal and conditional p.d.f of X and Y. Are X and Y independent ?
[A.U
Tvli M/J 2010] [A.U A/M 2017 R-13]
[A.U
N/D 2017 R-13] [A.U A/M 2019 (R17) PS]
Solution:

Example
2.1.29
The
joint p.d.f of two random variables X and Y is given by
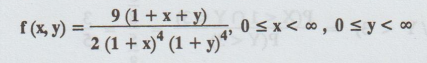
Find
the marginal distributions of X and Y, the conditional distribution of Y for X
= x and the expected value of this conditional distribution.
[A.U
Trichy M/J 2009] [A.U. A/M 2004, A/M 2011]
Solution:
(i) The marginal distribution of X is
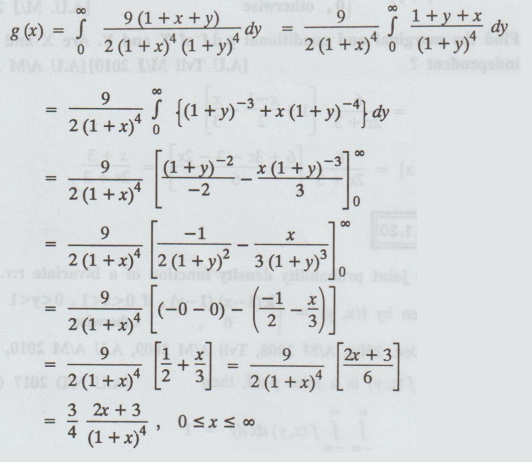
From
the form of the joint p.d.f of (X, Y). Similarly,
The
marginal distribution of Y is

Example
2.1.30
Find
k if the joint probability density function of a bivariate r.v.
(X,
Y) is given by f(x, y) =
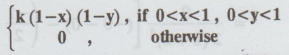
[AU Dec. 2006, A/M 2008, Tvli A/M 2009, A.U
A/M 2010, M/J 2014] [A.U N/D 2017 (RP) R-13]
Solution:
If
f (x, y) is a joint p.d.f, then
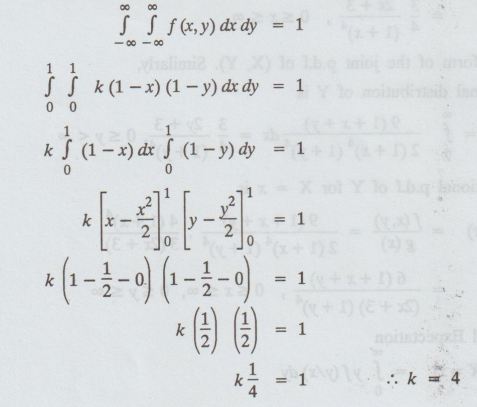
Probability and complex function: Unit II: Two dimensional random variables : Tag: : Two dimensional random variables - Problems under continuous random variables
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
