Problems under discrete random variables

PROBLEMS UNDER DISCRETE RANDOM VARIABLES :

Example 2.1.1

From, the following table for bivariate distribution of (X, Y) find

(i) P(X≤1),

(ii) P(Y≤ 3),

(iii) P(X ≤ 1, Y≤3),

(iv) P(X ≤ 1/Y≤ 3),

(v) P (Y≤ 3/X ≤ 1),

(vi) P (X + Y ≤ 4).

(vii) The marginal distribution of X or Marginal PMF of X

(viii) The marginal distribution of Y or Marginal PMF of Y

(ix) The conditional distribution of X given Y = 2

(x) Examine X and Y are independent. E[Y - 2X]

Solution :

Example 2.1.2

Let X and Y have the following joint probability distribution.

Show that X and Y are independent.

 Solution :

Example 2.1.3

The joint probability mass function of (X, Y) is given by P(x, y) = K(2x + 3y), x = 0, 1, 2; y = 1, 2, 3. Find all the marginal and conditional probability distributions. Also, find the probability distribution of (X + Y) and P[X + Y > 3].

[A.U. 2004]

[A.U N/D 2007, A.U N/D 2008, A.U. Tvli. A/M 2009, A.U N/D 2014]

[A.U CBT A/M 2011, N/D 2011, N/D 2013, A.U N/D 2015 R13 RP]

[A.U A/M 2017 R-13] [A.U N/D 2018 (R17) PS]

Solution:

Example 2.1.4

The joint probability distribution of a two-dimensional discrete random variable (X, Y) is given below :

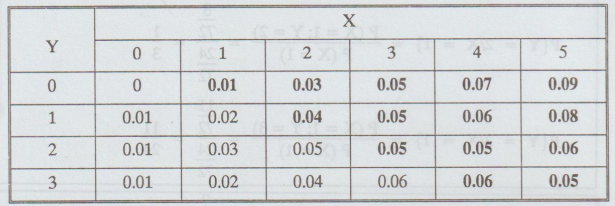
(i) Find, P(X > Y) and P{Max (X, Y) =

(ii) Find, the probability distribution of the random variable, Z = Min (X, Y)

Solution :

Example 2.1.5

The joint distribution of X and Y is given by f(x, y) = x + y/21 , x = 1, 2, 3, y = 1, 2. Find the marginal distribution. Also, find E[XY].  [A.U. N/D 2013]

Solution:

Example 2.1.6

The two dimensional random variable (X, Y) has the joint density function f(x, y) = x + 2y / 27 x = 0, 1, 2 ; y = 0, 1, 2. Find the conditional distribution  of Y given X = x. Also, find the conditional distribution of X given Y = 1. [A.U Tvli. A/M 2009] [A.U N/D 2017 R13-RP]

Solution:

Example 2.1.7

Three balls are drawn at random without replacement from a box containing 2 white, 3 red and 4 black balls. If X denotes the number of white balls drawn and Y denote the number of red balls drawn, find the joint probability of red balls distribution of (X, Y).

 [AU M/J 2007] [A.U A/M 2015 (RP) R-8] [A.U M/J 2016 RP R13]

Solution:

Three balls are drawn out of 9 balls.

X → number of white balls drawn.

Y → number of red balls drawn.

Example 2.1.8

Two discrete r.v.'s X and Y have the joint probability density function;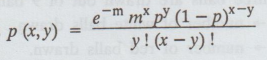 where m, p are constants with m > 0 and 0 < p < 1. Find (i) the marginal probability density function X and Y, (ii) the conditional distribution of Y for a given X and of X for a given Y. [A.U. N/D. 2005] [A.U Tvli. M/J 2010]

Solution:

Given the joint probability density function of the two discrete

random variables X and Y is p (x,y) = 

 (i) Then the marginal probability density function of X is,

which is a probability function of a Poisson distribution with parameter m.

which is the probability function of a Poisson distribution with parameter (mp).

(ii) The conditional distribution of Y for given X is,