Procedure for Solving Laplace's Equation

Procedure for Solving Laplace's Equation

AU : May-03,16,19, Dec.-16,18

• The procedure to solve a problem involving Laplace's equation can be generalized as,

Step 1 : Solve the Laplace's equation using the method of integration. Assume constants of integration as per the requirement.

Step 2 : Determine the constants applying the boundary conditions given or known for the region. The solution obtained in step 1 with constants obtained using boundary conditions is an unique solution.

Step 3 : Then   can be obtained for the potential field V obtained, using gradient operation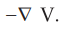 

Step 4 : For homogeneous medium, can be obtained as Ɛ  .

Step 5 : At the surface, ρs = D_N hence once  is known, the normal component DN to the surface is known. Hence the charge induced on the conductor surface can be obtained as .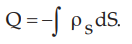

Step 6 : Once the charge induced Q is known and potential V is known then the capacitance C of the system can be obtained.

• If ρ v ≠ 0 then similar procedure can be adopted to solve the Poisson's equation.

 

Ex. 6.4.1 The region between two concentric right circular cylinders contains a uniform charge density p. Solve the Poisson's equation for the potential in the region.

AU : May-19, Marks 15

Sol. : The cylinders are shown in the Fig. 6.4.1.

Select the cylindrical co-ordinate system. In co-axial cable like structure, the electric field intensity   is in radial direction from inner to outer cylinder.

Hence   and V both are functions of only r and not of ϕ and z.

∂V / ∂r is existing while ∂ V / ∂ ϕ and ∂V / ∂z are zero,

According to Poisson's equation,

Knowing the boundary conditions, C₁ and C₂ can be obtained.

 

Ex. 6.4.2 Two parallel conducting discs are separated Toy distance 5 mm at z = 0 and z = 5 mm. If V = 0 at z = 0 and V = 100 V at z = 5 mm, find the charge densities on the discs.

AU : May-03, Marks 16

Sol. : The discs are shown in the Fig. 6.4.2.

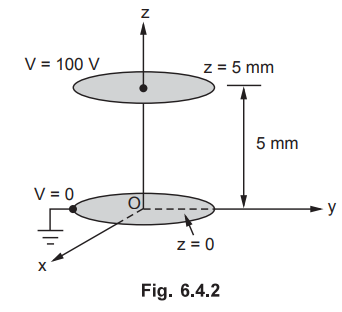
Consider cylindrical co-ordinates. The potential V is the function of z alone and is independent of r and ϕ.

This is the magnitude of surface charge densities on the discs. So ρs = ±177.08 nC/m², positive on upper plate and negative on lower plate.

Ex. 6.4.3 Find V at P (2, 1, 3) for the field of two infinite radial conducting planes with V = 50 V at ϕ = 10° and V = 20 Vat ϕ = 30°

Sol. : V is a function of $ only and not the function r and z.

 

Ex. 6.4.4 Find V at P (2, 1, 3) for the field of two co-axial conducting cones, with V = 50 V at θ = 30° and V = 20Vat θ = 50°.

Sol. : V is a function of 0 only and not the function of r and ϕ .

 

Ex. 6.4.5 In spherical coordinates V = - 25 V on a conductor at r = 2 cm and V = 150 V at r = 35 cm. The space between the conductor is a dielectric of Ɛr = 3.12. Find the surface charge densities on the conductor.

AU : Dec.-16, Marks 10

Sol. : The voltage is a function of r only in spherical system. Hence Laplace's equation is,

 

Ex. 6.4.6 In a charge free region of free space, a potential field is given as, V(x, y) = 5x³ + f(x)-2y² Find frx) if E_z and V are both zero at origin.

Sol. :

At origin, V(0, 0) = f(0) = 0

 

Ex. 6.4.7 Write Laplace's equation in cartesian co-ordinates and obtain the solution when V is function of x only for the boundary condition V = V₁ at x = x₁ and V = V₂ at x = x₂ .

Sol. : The Laplace's equation in cartesian co-ordinates is,

 

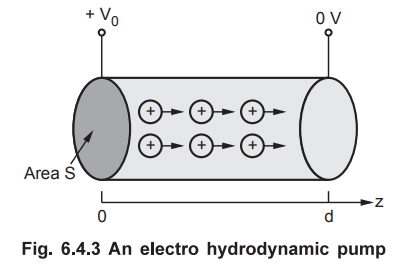
Ex. 6.4.8 Current carrying components in high-voltage power equipment must he cooled to carry away the heat caused by ohmic losses. A means of pumping is based on the force transmitted to the cooling fluid by charges in an electric field. The Electro Hydrodynamic (EHD) pumping is modelled in Fig. 6.4.3. The region between the electrodes contains a uniform charge ρ₀, which is generated at the left electrode and collected at the right electrode. Calculate the pressure of the pump if ρ0 = 25 mC/m³ and V₀ = 22kV.

Sol . :

Ρv = ρ0 ≠ 0 hence use Poisson’s equation,

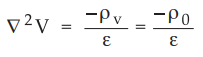
As V is a function of z only, the equations becomes,

Hence the required pressure for the pump is force per unit area,

 

Examples for Practice

Ex. 6.4.9 Given the volume charge density ρv  = -2×l0⁷ Ɛ0√|x C/m³ in free space, letV = 0atx = 0 and V = 2 V at x = 2.5 mm. Find V at x = 1 mm.

[Ans. : 0.30229 V]

Ex. 6.4.10 Using Poisson's equation, obtain the volume charge density pv inside a sphere of radius a if given field intensity is, E_r = Ar⁴ , for r < a and E_r = Ar^-2 , for r > a

[Ans. : 6 Aer3 Cm3, 0 C/m2]

Ex. 6.4.11 In spherical co-ordinates V = 0 at r = 0.1 m and V = 100 V at r = 2 m. Assuming free space between these concentric spherical shells, find .

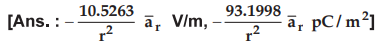
Ex. 6.4.12 An assembly of two concentric spherical shells is considered. The inner spherical shell is at a distance of 0.1 m and is at a potential of 0 volts. The outer spherical shell is at a distance of 0.2 m and at a potential of 100 V. The medium between them is a free space. Find  using spherical co-ordinate system.