Products of Three Vectors

Products of Three Vectors

• Let 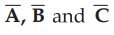 are the three given vectors. Then the product of these three vectors is classified in two ways called,

1. Scalar triple product 2. Vector triple product

1. Scalar Triple Product

• The scalar triple product of the three vector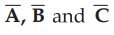s  is mathematically defined as,

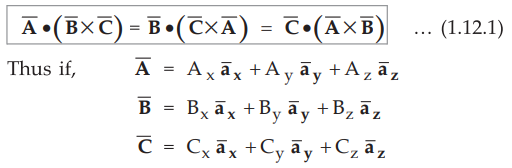
then the scalar triple product is obtained by the determinant,

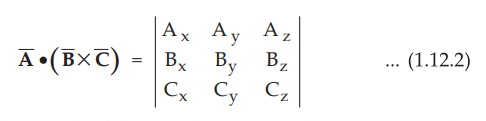
• The result of this product is a scalar and hence the product is called scalar triple product. The cyclic order a b c is important. 

a. Characteristics of Scalar Triple Product

1. The scalar triple product represents the volume of the parallelepiped with edges 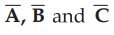 drawn from the same origin, as shown in the Fig. 1.12.1.

2. The scalar triple product depends only on the cyclic ‘ a b c’ and not on the position of the • and × in the product. If the cyclic order is broken by permuting two of the vectors, the sign is reversed.

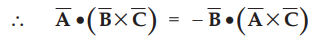
3. If two of the three vectors are equal then the result of the scalar triple product is zero.

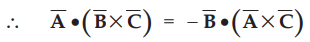
4. The scalar triple product is distributive.

2. Vector Triple Product

• The vector triple product of the three vector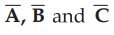s  is mathematically defined as,

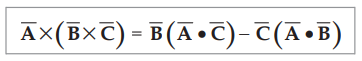......(1.12.3)

• The rule can be remembered as ‘bac-cab’ rule. The above rule can be easily proved by writing the cartensian components of each term in the equation. The position of the brackets is very important.

 a. Characteristics of Vector Triple Product

1. It must be noted that in the vector triple product,

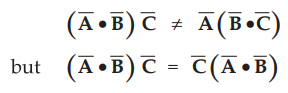
• This is because 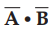 is a scalar and multiplication by scalar to a vector is commutative.

2. From the basic definition we can write,

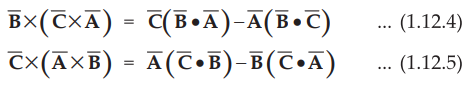
• But dot product is commutative hence 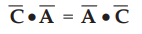 and so on. Hence addition of (1.12.3), (1.12.4) and (1.12.5) is zero.

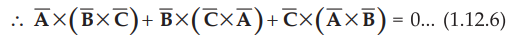
• The result of the vector triple product is a vector.

Ex. 1.12.1 The three fields are given by,

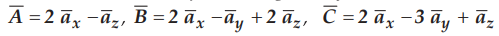
Find the scalar and vector triple product.

Sol. : The scalar triple product is,

Review Questions

1. Define scalar and vector triple product.

2. Prove that