Properties harmonic conjugates

PROPERTIES HARMONIC CONJUGATES

a. Laplace equation

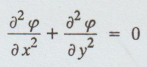 = 0 is known as Laplace equation in two dimensions.

b. Laplacian operator

∂²/∂x² + ∂²/∂y² is called the Laplacian operator and is denoted by .

Note (i) 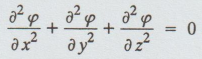 is known as Laplace equation in three dimensions.

Note (ii) The Laplace equation in polar coordinates is defined as

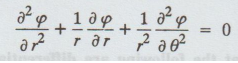
Property (1) The real and imaginary parts of an analytic function w = u + iv satisfy the Laplace equation in two dimensions viz 

[Anna, Nov 1996]

[OR] Prove that the real and imaginary parts of an analytic function are harmonic functions. [A.U M/J 2014] [A.U A/M 2019 (R17)] [A.U N/D 2019 (R17)]

Proof :

Let f (z) = u + iv be an analytic function

→ U_x = V_y  ...(1) and u_y = -V_x ....(2) by C-R

 Differentiate (1) & (2) p.w.r. to x, we get

U_xx = V_xy ......(3)and u_xy = -V_xx... (4) by C-R

Differentiate (1) & (2) p.w.r. to y, we get

U_yx = v_yy ....(5) and u_yy = -V_yx... (6)

 (3) + (6) ⇒ u_xx + u_yy  = 0 [ v_xy = v_yx ]

 (5) - (4) ⇒ V_xx + V_yy = 0 [u_xy = u_yx ]

 u and v satisfy the Laplace equation.

Note: Converse of the property need not be true.

Example: u = x² - y²  , v = -y / x² + y²

Harmonic function or [Potential function]

A real function of two real variables x and y that possesses continuous second order partial derivatives and that satisfies Laplace equation is called a harmonic function.

Note: A harmonic function is also known as a potential function.

Conjugate harmonic function

If u and v are harmonic functions such that u + iv is analytic, then each is called the conjugate harmonic function of the other.

Property (2) The real and imaginary parts of an analytic function w = u(r, θ) + iv (r, θ) satisfy the Laplace equation in polar coordinates.

Proof : Given: w =  u (r, θ) + iv (r, θ) is an analytic function.

u and v satisfy C-R equations

i.e., ∂u/∂r = 1/r ∂v/∂θ .....(1)

∂v/∂r = -1/r ∂u/∂θ ....(2)

Differentiate (1) p.w.r. to r, we get

∂²u/∂r² = 1/r ∂²v/∂r∂θ – 1/r² ∂v/∂θ ......(3)

Differentiate (2) p.w.r. to θ, we get

∂²v/∂θ∂r = -1/r ∂²u/∂θ² ......(4)

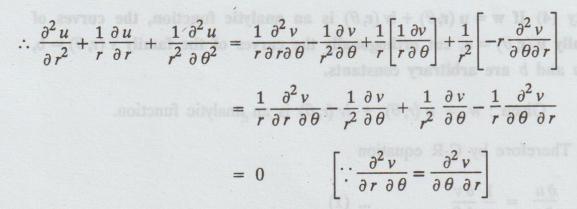
Thus u satisfies Laplace equation in polar coordinates.

Similarly, v also satisfies Laplace equation in polar coordinates.

Property (3) If w = u(x, y) + iv (x, y) is an analytic function the curves of the family u (x, y) = a and the curves of the family v (x, y) = b cut orthogonally, where a and b are varying constants. [A.U A/M 2019 (R13)]

[or]

When the function f(z) = u + iv is analytic, show that u = constant and v = constant are orthogonal. (Anna, May 1999] [Anna, Oct 1997] [Anna, May 2001] [A.U D15/J16 R-13] [A.U N/D 2016 R-13] [A.U A/M 2017 R-08]

Proof :

Let f (z) = u + iv be an analytic function.

⇒ u_x = v_y ... (1) and u_y = -v_x (2) by C-R

Given: u = a and v = b

Differentiate p.w.r. to x, we get

⇒ u_x + u_y dy/dx = 0 and v_x + v_y dy/dx = 0

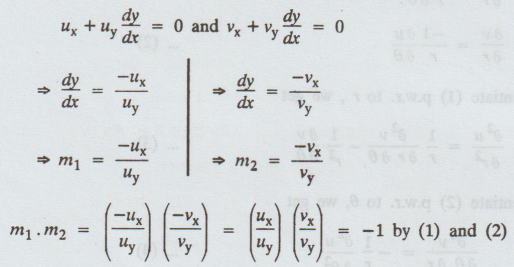
Hence, the family of curves form an orthogonal system.

Property (4) If w = u (r, θ) + iv (r, θ) is an analytic function, the curves of the family u (r, θ) = a, cut orthogonally the curves of the family v (r, θ) = b, where a and b are arbitrary constants.

Proof :

Given: w = u(r,θ) + iv (r, θ) is an analytic function.

Therefore by C-R equation

∂u/∂r = 1/r ∂v/∂θ .....(1)

∂v/∂r = -1/r ∂u/∂θ .....(2)

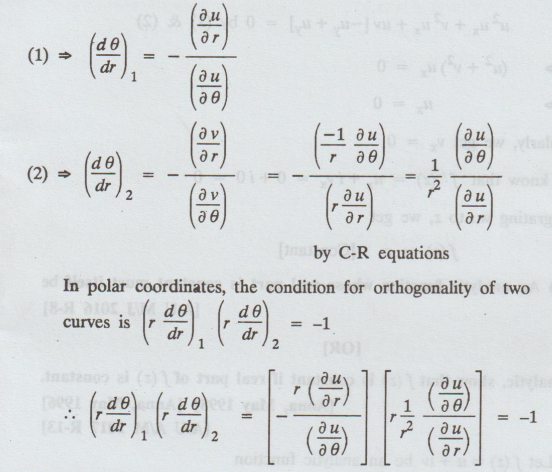
Hence, the two family of curves form an orthogonal system.

Property 5. An analytic function with constant modulus is constant. [AU. A/M 2007] [A.U N/D 2010 R-8] [A.U M/J 2016 R-8]

Proof :

Let f (z) = u + iv be an analytic function.

⇒ u_x = v_y ... (1) and u_y = -v_x (2) by C-R.

Given: | f (z) |= √u² + V² =  c ≠ 0

→ |f(z) |² = u² + v² = c²(say)...

i.e., u² + y² = c²... (3)

Differentite (3) p.w.r. to x and y; we get

2uu_x + 2vv_x = 0 ⇒ uu_x + vv_x = 0 ...(4)

2uu_y +  2vv_y = 0 ⇒ uu_y + vv_y = 0 ...(5)

Similarly, we get v_x = 0

We know that f'’ (z) = u_x + iv_x = 0 + i0 = 0

Integrating w.r.to z, we get

f(z) = c [Constant]

Property (6) An analytic function whose real part is constant must itself be a constant.  [A.U M/J 2016 R-8]

 [OR]

If f (z) is analytic, show that f (z) is constant if real part of f (z) is constant. [Anna, May 1998] [Anna, May 1996] [A.U A/M 2017 R-13]

Proof :

Let f (z) = u + iv be an analytic function

→ u_x = v_y ... (1) and u_y = -v_x ..(2) by C-R.

Given : u = c [Constant]

⇒u_x = 0 , u_y = 0

v_x = 0 by (2)

We know that, f' (z) = u_x + iv_x

= 0 + i0

= 0

Integrating w.r.to z, we get f (z) = c [Constant]

Property (7) Prove that an analytic function with constant imaginary part is constant. [A.U M/J 2005]

Proof: Let f (z) = u + iv be an analytic function.

u_x = v_y ... (1) and u_y= -v_x ... (2) by C-R.

Given: v = c [Constant]

=> v_x = 0, v_y = 0

We know that, f' (z) = u_x + iv_x

= v_y + iv_x by (1)

= 0 + i0

i.e., f' (z) = 0

Integrating w.r.to z, we get f (z) = c [Constant]

Property (8) If f (z) and 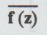 are analytic in a region D, then show that f(z) is constant in that region D.

Proof: Let f (z) = u (x,y) + iv (x,y)

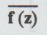= u (x,y) – iv (x,y) = u (x, y) + i[-v (x,y)]

Since, f (z) is analytic in D, we get u_x = v_y and u_y = -v_x

Since, 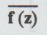 is analytic in D, we have u_x = -v_y and u_y = v_x

Adding, we get u_x = 0 and u_y = 0 and hence, v_x = v_y = 0

 f' (z) = u_x + ivx = 0 + i0 = 0

 f (z) is constant in D.