Recursive Functions

Recursive Functions

AU: Dec.-18,19, Marks 13

Definition: Recursion is a programming technique in which the function calls itself repeatedly for some input.

By recursion the same task can be performed repeatedly.

Properties of Recursion

Following are two fundamental principles of recursion

1. There must be at least one condition in recursive function which do not involve the call to recursive routine. This condition is called a "way out" of the sequence of recursive calls. The is called base case property.

2. The invoking of each recursive call must reduce to some manipulation and must go closer to base case condition.

While computing factorial using recursive method -

if(n= =0)

return 1; //This is a base case

else

return n*fact (n-1);//on each call the computation will go closer to base case

 

1. Factorial

Algorithm for Factorial Function using Iterative Definition

1. prod = 1;

2. x=n;

3. while(x>0)

4. {

5. prod = prod*x;

6. X - - ;

7. }

8. return(prod);

 

Algorithm for Factorial Function using Recursive Definition

1. if(n==0)

2. fact =1;

3. else

{

4. x-n-1;

5. y= value of x!;

6. fact = n* y;

7. } /*else ends here */

This definition is called the recursive definition of the factorial function. This definition is called recursive because again and again the same procedure of multiplication is followed but with the different input and result is again multiplied with the next input. Let us see how the recursive definition of the factorial function is used to evaluate the 5!

Step 1. 5! = 5* 4!

Step 2. 4! = 4* 3!

Step 3. 3! = 3 * 2!

Step 4. 1! = 1 * 0!

Step 5. 2! = 2 * 1!

Step 6. 0! = 1.

Actually the step 6 is the only step which is giving the direct result.So to solve 5! we have to backtrack from step 6 to step 1,collecting the result from each step. Let us see how to do this.

Step 6'. 0! =1

Step 5'. 1!= 1*0! = 1 from step 6'

Step 4'. 2! 2*1! = 2 from step 5'

Step 3'. 3! = 3*2! = 6 from step 4'

Step 2. 4! 4*3! = 24 from step 3'

Step 1'. 5!= 5*4! = 120 from step 2'

 

Ex. 1.9.1 Write a C program to find factorial of a number. Using recursive function.

AU: Dec.-18, Marks 6

Solution :

 /*****************************

Program for finding out the factorial for any given number.

******************************/

#include<stdio.h>

#include<stdlib.h>

#include<conio.h>

void main(void)

{

int n,f;

int fact(int n);/* declaration*/

clrscr( );

printf("\n\t\t Program For finding the factorial of n");

printf("\n\n Enter the number for finding the factorial: ");

scanf("%d", &n);

f=fact(n);/*call to fucntion*/

printf("\n the factorial of %d is %d",n,f);

getch( );

}

int fact(int n)

{

int x,y;

if(n<0)

{

printf("The negative parameter in the factorial function");

exit(0);

}

if(n= =0)

return 1;

x = n-1;

y=fact(x); /*recursive call*/

return(n*y);

}

Output

Program For finding the factorial of n

Enter the number for finding the factorial: 5

the factorial of 5 is 120

 

2. GCD (Greatest Common Divisor)

In this method the GCD is calculated using following function

gcd (a,b)=gcd(b,a mod b)   provided a>b

when we get gcd(a,0)

then

GCD = a

Consider there are two numbers 30 and 18 then we can find GCD as follows -

The above table itself illustrates the procedure for finding GCD using Euclid's algorithm.

The algorithm in simple steps can be given as -

Step 1: Divide a by b and assign the value of remainder to variable c.

Step 2: Then assign the value of b to a and value of c (remainder of a/b) to b.

Step 3: Repeat the steps 1 and 2 until value of b becomes 0.

Step 4: If b=0 then return value of a as the GCD value of a and b.

Step 5: Stop.

C program

/************************************

Program to find out the greatest common divisor of the two integers.

************************************/

#include< stdio.h >

#include< conio.h >

#include< stdlib.h >

void main(void)

{

int a,b,ans;

int gcd(int a,int b);

clrscr();

}

printf("\n\t\t GCD Of two integers");

printf("\n\n Enter the two numbers: ");

scanf("%d %d",&a,&b);

ans=gcd(a,b);

printf("\n The gcd of %d and %d is = %d",a,b,ans);

getch( );

}

int gcd(int a,int b)

{

int temp,ans;

if( b< = a &&a%b = =0)

return b;

else

{

if(a<b)

return(gcd(b,a));

/*the divisior should be less than divident*/

else

ans = a%b;

return(gcd(b,ans));

}

}

Output

GCD Of two integers

Enter the two numbers: 12 15

The gcd of 12 and 15 is = 3

 

3. Fibonacci Sequence

The Fibonacci sequence is the sequence of integers

Each number in this sequence is the sum of two preceding elements.

For example the series can be formed in this way

0+1 = 1, ----à 0^th element + 1^st element

1+1= 2, ----à 1^st element + 2^nd element

1+2= 3, ----à 2^nd element + 3^rd element

2+3 = 5, ----à 3^rd element + 4^th element

3+5 = 8, ----à 4^th element + 5^th element

Let fib(0) = 0,fib(1) = 1,We can define the recursive definition of Fibonacci sequence by the recursive definition :

fib(n) = n if n==0 or n==1 … (1)

fib(n) = fib(n-2)+ fib(n-1)if n>=2 …(2)

Let us apply this definition to compute fib(6)

fib(6) = fib(4) +fib(5) using definition (2)

but  fib(4) = (fib(2)+fib(3))

fib(6) = (fib(2)+fib(3)) +fib(5)

= (fib(0)+fib(1))+fib(3)+fib(5) ……… where fib(2) is fib(0)+fib(1)

= 0+1+fib(3)+fib(5) ……. fib(0)=0 and fib(1)=1

= 1+fib(1)+fib(2)+fib(5) …….. where fib(3) is fib(1)+fib(2)

= 1+1+fib(2)+fib(5) …….. .fib(1) is 1 and fib(2)

= fib(0)+fib(1)

= 2+fib(0)+fib(1)+fib(5)

= 2+0+1+fib(5)

= 3+fib(5)

= 3+fib(3)+fib(4)

= 3+fib(1)+fib(2)+fib(4)

= 3+1+fib(2)+fib(4)

= 4+fib(0)+fib(1)+fib(4)

= 4+0+1+fib(4)

= 5+fib(4)

= 5+fib(2)+fib(3)

= 5+fib(0)+fib(1)+fib(3)

= 5+0+1+fib(3)

= 6+fib(1)+fib(2)

= 6+1+fib(2)

= 7+fib(0)+fib(1)

= 7+0+1

Hence fib(6) = 8

Here the recursive definition appears twice e.g. fib(6)=fib(4)+fib(5).

Algorithm for Fibonacci series by recursive method :

int fib(int n)

{

int x,y;

if(n< = 1)

return n;

x = fib(n-1);

y = fib(n-2);

return (x+y);

}

Algorithm for Fibonacci series by iterative method :

if(n< = 1)

return (n);

a = 0;

b = 1;

for(i = 2;i<  =n;i++)

{

x=a;

a=b;

b=x+a;

}

return (b);

C Program

/*******************************************************

Program for computing the number in the fibonacci series at certain location.For e.g.the sixth number in fibonacci series will be 8.The fibonacci series is 1 1 2 3 5 8 13 21 34...

**********************************************************/

/*header files*/

#include<stdio.h>

#include<conio.h>

 

void main(void)

{

int n,num;

int fib(int n);

clrscr( );

printf("\n Enter location in fibonacci series: ");

scanf("%d",&n);

num=fib(n);

printf("\n The number at %dth position is %d in fibonacci series",n,num);

getch();

}

int fib(int n)

{

int x,y;

if(n< = 1)

return n;

x = fib(n-1);

y = fib(n-2);

return (x+y);

}

/**************** End of Program ****************/

Output

Enter location in fibonacci series: 9

The number at 9th position is 34 in fibonacci series

 

4. Tower of Hanoi

The problem is the "Towers of Hanoi". The initial setup is as shown in Fig. 1.9.1.

There are three pegs named as A,B and C. The five disks of different diameters are placed on peg A. The arrangement of the disks is such that every smaller disk is placed on the larger disk.

The problem of "Towers of Hanoi" states that move the five disks from peg A to peg C using peg B as a auxillary.

The conditions are :

i) Only the top disk on any peg may be moved to any other peg.

ii) A larger disk should never rest on the smaller one.

The above problem is the classic example of recursion. The solution to this problem is very simple.

First of all let us number out the disks for our comfort

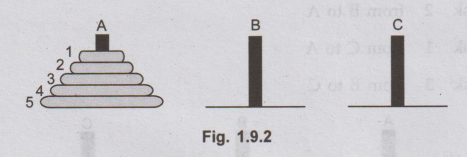
The solution can be stated as

1. Move top n-1 disks from A to B using C as auxillary.

2. Move the remaining disk from A to C.

3. Move the n-1 disks from B to C using A as auxillary.

We can convert it to

move disk 1 from A to B.

move disk 2 from A to C.

move disk 1 from B to C.

move disk 3 from A to B

move disk 1 from C to A

move disk 2 from C to B

move disk 1 from A to B

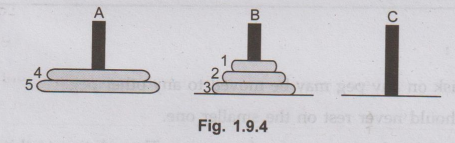
move disk 4 from A to C

move disk 1 from B to C

move disk 2 from B to A

move disk 1 from C to A

move disk 3 from B to C

move disk 1 from A to B

move disk 2 from A to C

move disk 1 from B to C

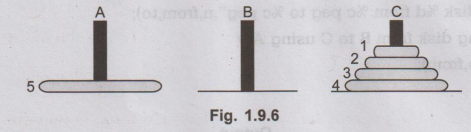
Thus actually we have moved n-1 disks from peg A to C. In the same way we can move the remaining disk from A to C.

'C' Program

/******************************************************

Program For Towers of Hanoi. The input will be the number of disks for which the program should operate.

*******************************************************/

#include<stdio.h>

#include<conio.h>

#include<stdlib.h>

void main(void)

{

int n;

void towers (int n,char from, char to,char aux); clrscr();

printf("\n\t\t Program For Towers Of Hanoi");

printf("\n\n Enter the total number of disks");

scanf("%d",&n);

towers(n,'A','C', 'B');

getch();

}

void towers (int n,char from, char to,char aux)

{

/*if only one disk has to be moved*/

if(n = =1)

{

printf("\n Move disk 1 from %c peg to %c peg", from,to);

return;

}

/*move top n-1 disks from A to B using C*/

towers(n-1,from,aux,to);

printf("\n Move disk %d from %c peg to %c peg",n,from,to);

/* move remaining disk from B to C using A*/

towers(n-1,aux,to,from);

}

Output

Program for Towers of Hanoi

Enter the total number of disks 4

 

Move disk 1 from A peg to B peg

Move disk 2 from A peg to C peg

Move disk 1 from B peg to C peg

Move disk 3 from A peg to B peg

Move disk 1 from C peg to A peg

Move disk 2 from C peg to B peg

Move disk 1 from A peg to B peg

Move disk 4 from A peg to C peg

Move disk 1 from B peg to C peg

Move disk 2 from B peg to A peg

Move disk 1 from C peg to A

Move disk 3 from B peg to C

Move disk 1 from A peg to B peg

Move disk 2 from A peg to C peg

Move disk 1 from B peg to C peg

 

5. Ackerman's Recursive Function

The Ackerman's recursive formula is as given below

• A(0, n): n + 1 for n ≥0

• A(m, 0):= A(m - 1, 1) for m > 0

• A(m, n): A(m - 1, A(m, n - 1)) for m, n > 0

 

Ex. 1.9.2. Solve A (2, 1) using Ackerman's function

Solution :

Here m = 2, n = 1

A (2, 1) = A (m-1, A (m, n − 1))

= A (1, A (2, 0))

= A (1, A (2-1, 1))

= A (1, A (1, 1))

= A (1, [A(1-1, A (1, 0))])

= A (1, A (0, A (1, 0)))

=A (1, A (0, A (0, 1)))

= A (1, A (0, 2))

= A (1, 3) …. (1)

= A (1, 3) = A (1 - 1, A (1, 3 - 1))

= A (0, A (1, 2))

= A (0, A (1-1, A (1, 2 - 1)))

= A (0, A (0, A (1, 1)))

= A (0, A (0, A (1-1, A (1, 1- 1))))

= A (0, A (0, A (0, A (1, 0)))).

= A (0, A (0, A (0, A (0, 1))))

= A (0, A (0, A (0, 2)))

= A (0, A (0, 3))

A (1, 1) = A (0, 4) = 5 … (2)

Putting value of equation (2) in (1)

A (2, 1) = 5

 

Ex. 1.9.3 Compute A(1,1) using Ackerman's formula.

Solution:

Let us compute A(1,1)

A(1,1) = A(m-1,A(m,n-1)) = A(0,A(1,0))

= A(0,A(m-1,1))

= A(0,A(0,1) …. (1)

A(0,1) = n+1=2

Putting this value in equation (1) we will get

A(1,1) = A(0,2)= n+1 = 3

C Function

int ackerman(int m, int n, int &count)

C Program

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

int ackerman(int m, int n, int &count)

{

count++;

if (m = = 0)

}

return (n + 1);

}

if (n = = 0 && m>0)

{

return ackerman(m - 1, 1, count);

}

if (m>0 && n>0)

{

return ackerman(m - 1, ackerman(m, n - 1, count), count);

}

}

int main( )

{

int m, n;

printf("\n Enter value of m: ");

scanf("%d", &m);

printf("\n Enter value of n: ");

scanf("%d", &n);

int count = 0;

printf("%d", ackerman(m, n, count));

}

Output

Enter value of m: 2

Enter value of n: 1

5

 

6. Comparison between Iteration and Recursion

Review Question

1. Explain recursion and write a C program to print the first 'n' numbers in the Fibonacci series using recursion.

AU: Dec.-19, Marks 13