Reflection of Uniform Plane Waves

Reflection of Uniform Plane Waves

AU : Dec.-05,06,14,16,17,19, May-08,15,16,17

• We have, so far, studied the uniform plane waves travelling in unbounded and homogeneous media. But practically, very often, waves propagate in bounded regions consisting several media of different constitutive parameters such as Ɛ, µ, σ, ɳ etc. Before we actually start with the reflection of the uniform plane wave, let us consider simple example of a transmission line.

• Consider a transmission line having a characteristic impedance Z₀. Assume that a line is terminated in load impedance Z_L .

If the load impedance Z_L equals the characteristic impedance Z₀ (i.e. Z_L = Z₀), then the line is said to be properly terminated.

• If Z_L ≠ Z₀, then there is a mismatch between the two impedances and the line is not properly terminated. Consider that the wave travelling along the line incidents at the load. The part of the wave gets absorbed by the load ; while other part is reflected back to the generator. So we can say reflection occurs at the load if Z_L ≠ Z₀. If there are two waves ; one incident in forward direction, while other reflected back in backward direction, then the standing waves are said to be produced along the line.

• Now consider again the uniform plane wave travelling in non-homogeneous media. When a uniform plane wave travels from one medium to other having different intrinsic impedances, the reflection takes place at the boundary. The part of the wave is transmitted in medium 2 and remaining part is reflected back to medium 1, depending upon the constitutive parameters of media. Depending upon the manner in which the uniform plane is incident on the boundary, there are two cases of incidence.

i) Normal incidence : When a uniform plane wave incidences normally to the boundary between the media, then it is known as normal incidence.

ii) Oblique incidence : When a uniform plane wave incidences obliquely to the boundary between the two media, then it is known as oblique incidence.

In this section we shall focus on the interface between,

i) Two dielectric media and

ii) Dielectric and conductive media.

 

1. Normal Incidence at Plane Dielectric Boundary

• Consider a uniform plane wave striking the interface between the two dielectrics at right angles as shown in the Fig. 10.10.1.

• Assume that a uniform plane wave travels along +z direction and incidence at right angles at the boundary between two dielectric media i.e. at z = 0. Below z = 0, let the properties of medium 1 be Ɛ₁, µ₁, σ₁, ɳ₁ and above z = 0, the properties of medium 2 be Ɛ₂, µ₂, σ₂, ɳ₂. So depending upon the properties of two media, part of the wave will be transmitted in medium 2 while other part will be reflected back in medium 1.

• Let E_i and H_i be the field strengths of the incident wave striking the boundary. Let E_t and H_t be the field strengths of the transmitted wave in the medium 2. And let E and H_r be the field strengths of the reflected wave in the medium 1 returning back from the interface.

• From the Fig. 10.10.1 it is clear that in medium 1, the total field comprises both the incident and reflected fields. But in medium 2, only the transmitted field gives the total field. So the conditions for the total fields in medium 1 are given by,

• Similarly the conditions for the total fields in medium 2 are given by, 

• According to the boundary conditions, the tangential components of  and  must be continuous at the interface z = 0. As we know the waves are transverse in nature, at the boundary we get both the fields  and  both tangential to the interface.

• Thus at the interface z = 0, we can write

• The relationships between the magnitudes of   and at z = 0 are given by following expressions.

E_i = η₁ H_i,

E_r = - η₁ H_r

.... As direction of reflected wave is opposite to that of incident wave

E_t = η₂ H_t

Interms of magnitudes of the fields  and  at the interface, we can write,

E_i + E_r = E_t ... (10.10.1)

and    H_i + H_r = H_t          ... (10.10.2)

• In equation (10.10.2), putting values of H_i, H_r and H_t interms of E, E_r and E_t respectively,

• Adding equations (10.10.1) and (10.10.3),

• The transmission coefficient is denoted by r and it is given by,

τ = E_t / E_i = 2 η₂ / η₁ + η₂

• Eliminating E_t from equations (10.10.1) and (10.10.3), we get,

• The reflection coefficient is denoted by T and it is given by,

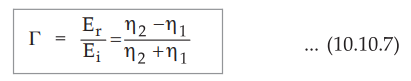
• From equations (10.10.5) and (10.10.7), we can draw some important results as,

a) 1 + ɼ = τ

b) 0 ≤ | ɼ | ≤ 1

c) Both the coefficients ; ɼ and τ are dimensionless and may be complex in nature.

• According to Poynting theorem, the average power density is given by,

P_avg = 1/2 E²_m/ɳ W/m²

• Where E_m is the amplitude of the electric field intensity and η is the intrinsic impedance of a medium.

• The average power transmitted in medium 1 is given by,

• The average power reflected in medium 1 is given by,

• Similarly the average power transmitted in medium 2 is given by, 

 

2. Normal Incidence at Plane Conducting Boundary

• Consider a uniform plane wave striking the interface between two media ; where medium 1 is perfect dielectric (σ = 0, lossless) and medium 2 is perfect conductor (σ = ∞). For medium 2, intrinsic impedance ɳ2 = 0 being a perfect conductor. Thus the transmission coefficient is given by,

τ = 2η₂ / η₁ + η₂ = 0 … (10.10.11)

• Also the reflection coefficient is given by,

τ = 2η₂ – η₁ / η₂ + η₁ = -1 … (10.10.12)

• From the values of the reflection and transmission coefficients it is clear that the wave is totally reflected and there is no transmitted wave in medium 2. It is obvious from the fact that no field can exists in the perfect conductor. As totally reflected wave combines with the incident wave, standing waves are formed.

• A standing wave does not travel and it consists of two travelling waves; one incident () and other reflected (). Both the waves have same amplitudes but the directions in which they propagate are different.

•  Let the standing wave in medium be denoted by . Thus in phasor form we can write,

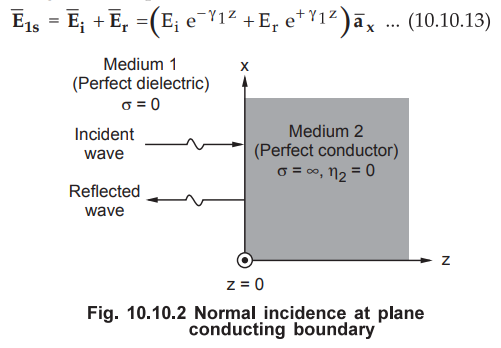
But as the reflection coefficient is

ɼ = E_r / E_i = -1

• Also for medium 1, σ = 0 indicates perfect dielectric medium.

• Exactly similar to above derivation, we can obtain magnetic field  in medium 1 as

• From equations (10.10.17) and (10.10.18) it is clear that the total fields in the medium 1 are not travelling eventhough these fields are obtained by adding two waves of equal amplitude but travelling in opposite directions. Also in these two equations, the factors with time and distance are represented by separate trigonometric terms.

• Consider the equation for total electric field in medium 1 given by equation (10.10.17). This field is zero everywhere whenever ωt = n π . Also this field is zero for all time at the planes for which β1 z = n π.

• The planes at which the electric field is zero are located where,

• The above condition clearly indicates that the electric field is zero at z = 0 and it repeats after every half wavelength from the boundary in the medium 1 where z < 0. The Fig. 10.10.3 shows the instantaneous values of the electric field in medium 1 at t = π/2

 • Now consider equation (10.10.18) representing a standing wave. The magnitude of the magnetic field is maximum at the positions where the electric field is zero. Furthermore it is 90° out of time phase with the electric field everywhere.

a. Standing Wave Ratio (SWR)

• In the last section we have studied that the electric field is zero at boundary and repeats at every half wavelength distance from boundary in medium 1 (z < 0). At the same time, the magnitude of the magnetic field is maximum at the positions where the electric field is zero. By using a simple probe, relative amplitudes of electric or magnetic field intensity are easily measured. By using a small coupling loop, amplitude of the magnetic field can be measured. While by using a simple co-axial cable, amplitude of the electric field can be measured. To measure actual indication, the output of the probe is connected to either microammeter, millivoltmeter or any special display device.

• Consider a uniform plane wave travelling in a lossless medium with no reflected wave present in the medium. It is observed that the relative amplitude of the field is same at every point. It is obvious that the instantaneous field undergoes phase change of β (z2 -z1) when the probe is moved from z = z1 to z = z2 along a wave. Thus we can conclude that unattenuated travelling wave shows equal amplitude voltages characteristic.

• Now consider a uniform plane wave travelling in a lossless medium ; it gets reflected back by the perfect conductor. This results in the generation of standing wave. When the voltage probe is located at the interface i.e. z = 0 and at every integral number of half wavelengths from the interface in medium 1 (z < 0) ; the output of the probe will be zero. When the position of probe is changed, the amplitude of the field varies as |sinβ z| as shown in the Fig. 10.10.4.

• Note that z is the distance from the interface.

• The total field in medium 1 is obtained by adding incident and reflected field intensities. Thus the total field in medium 1 along standing wave is given by,

• Let the medium 1 be perfect dielectric. So σ = 0 and ɑ = 0. Thus the propagation constant is ɤ = jβ Also the reflection coefficient is given by, 

• Then the total field in medium 1 is given by,

• The reflection coefficient can be expressed interms of intrinsic impedances of the two media as,

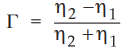
• As we have already studied that, r may be complex ; so we can write the reflection coefficient in phasor form as,

• Here depending upon the nature and values of  η1 and η2 we get three conditions for an angle ϕ

i) If medium 2 is perfect conductor, ϕ  = π

ii) If η₂ is real and η₂ < η₁ ; ϕ = π

iii) If η₂ is real and η₂ < η₁ ; ϕ = 0

• Then the total field in the region is given by,

• Let us check out the conditions for the maximum and minimum values of the magnitude.

• It is obvious that when the incident and reflected waves are in phase, we get maximum amplitude of the field. That means the phase angle of both the waves is same.

• And this maxima occurs where,

• Consider that η₁ and η₂ both are real and η₂ and η₁ . Then we get voltage maximum at interface (i.e. z = 0) if ϕ = 0.

• If the interface is between a perfect dielectric and a perfect conductor, then ϕ = π Then the voltage maximum occurs at

- β1z = π/2, 3π/2  and so on

• When incident wave and reflected wave are out of phase by 180°, we get minimum voltage.

And this minima occurs where 

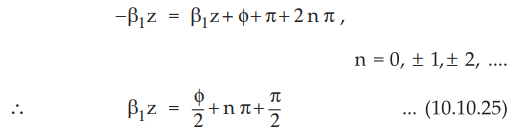
• From the equation (10.10.25) it is clear that the voltage minima are separated by λ /2 distance. Thus voltage minima occurs at - β1z = 0 for perfect conductor.

• In general voltage minima are separated by one half wavelength. Also the voltage maxima are also separated by one half wavelength.

• The standing wave ratio (S) is defined as the ratio of maximum to minimum amplitudes of voltage.

• When the amplitudes of reflected and incident waves are equal,  | ɼ | = 1. Thus s is infinite indicating total energy is reflected.

• When there is no reflection of energy i.e. η₂ = η₁ then ɼ = 0. Thus s is unity.

• The standing wave ratio s is dimensionless and the value of s lies in the range

1 ≤ s ≤ ∞.

• We can express reflection coefficient (r) interms of the standing wave ratio as,

|ɼ| = S – 1 / S + 1  ...(10.10.27)

 

Ex. 10.10.1  and  waves, travelling in free space, are normally incident on the interface with a perfect dielectric with Ɛr =3. Compute the magnitudes of incident, reflected and transmitted  and  waves at the interface.

Sol. : For medium 1, i.e. free space,

η1 = 120π = 377 Ω

For medium 2, i.e. perfect dielectric,

 

Ex. 10.10.2 Determine the amplitudes of reflected and transmitted fields (electric and magnetic both) at the interface of two regions, if Ei = 1.5 mV/m in region 1 for which Ɛr1 = 8.5, µr = 2 and σ  = 0 and region 2 is a free space.

AU : Dec.-05, Marks 8

Sol. : The interface is between perfect dielectric (region 1) and free space (region 2).

Ex. 10.10.3 A free space-silver interface has E (incident) = 100 Vhn on the free space side. The frequency is 15 MHz and the solve constants are Ɛr = µr =1 σ = 617 MS/m Determine E (reflected), E (transmitted) at the interface.

AU : Dec.-06, May-17, Marks 8

Sol. : The conductivity of silver is given as a = 61.7 MS/m >> 1, it can be considered as good conductor.

Thus the intrinsic impedance for good conductor is given by,

Key Point : Note that 180° angle represents that the wave propagates in opposite direction to that of the incident wave. E_r is almost equal to Ei indicates that the wave cannot propagate in good conductor but gets totally reflected.

 

Ex. 10.10.4 Determine the amplitude of the reflected and transmitted E and H at the interface of two media with the following properties. Medium 1 :t:.Ɛr = 8.5,µr =1 σ = 0 Medium 2; free space. Assume normal incidence and the amplitude of E in the medium 1 at the interface is 1.5 mV/m.

AU : Dec.-05, Marks 8

Sol. : The interface is between perfect dielectric (region 1) and free space (region 2).

 

Ex. 10.10.5 A plane wave travelling in +z direction in free space (z < 0) is normally incident at z = 0 on a conductor (z > 0) for which σ = 61.7 MS/m, µr = 1. The free space E wave has a frequency f = 1.5 MHz and an amplitude of 1.0 V/m at the interface it is given by  Analyse the wave and predict magnetic wave  (0, t) at z > 0.

Sol. :

For z > 0, in complex form,

 

Ex. 10.10.6 A plane wave travelling in air is normally incident on a block of paraffin with Ɛr = 2.2. Find the reflection coefficient.

AU : May-15, Marks 4

Sol. : Medium 1 : Air i.e. free space.

Hence η₁ = η₂ = 377 Ω

Medium 2 : Paraffin with Ɛ_r = 2.2, µ_r = 1.

 

Examples for Practice

Ex. 10.10.7 In free space (Z ≤ 0) a plane wave with  is incident normally on a lossless medium (Ɛ = 2 Ɛo, µ = 8µo) in region Z ≥ 0. Determine reflected wave 

[Ans.: 6.669 × 10^-3 A/m, - 3.33 × 10^-3 A/m, - 5025.41 cos (10⁸t-β₂z)  mV/m ] 

Ex. 10.10.8 A travelling   field in the free space of amplitude 100 V/m, strikes a perfect dielectric, as shown in the Fig. 10.10.8. Determine E_t.

[Ans.: 59.7125 V/m]

Review Questions

1. Explain reflection of uniform plane waves with normal incidence at a plane dielectric boundary.

AU: May-16, Dec.-19, Marks 10

2. Obtain solution for a uniform plane wave in an isotropic homogeneous dielectric medium.

3. Derive the transmission and reflection coefficients for the electromagnetic waves.

AU May-08, Marks 8

4. Derive the transmission and reflection coefficients at the interface of two media for normal incidence.

AU: Dec.-06, Marks 8

5. Briefly explain about wave incident normally on perfect conductor.

AU: Dec.-14, Marks 8

6. Write a note on standing wave ratio.

AU: Dec.-14, 17, May-16, Marks 6