Regression: Example Solved Problems

Example 2.3.1

From the following data, find (i) the two regression equations, (ii) the coefficient of correlation between the marks in Economics and statistics, (iii) the most likely marks in Statistics when marks in Economics are 30.

 [A.U M/J 2007]

Solution :

 (iii) The most likely marks in statistics (y) when marks in Economics (x) are 30

i.e., y = -0.6643 x + 59.2575

x = 30 ⇒ y = 39

Example 2.3.2

The two lines of regression are

8x - 10y + 66 = 0 … (A)

40x - 18y - 214 = 0 … (B)

The variance of x is 9. Find (i) The mean values of x and y (ii) Correlation co-efficient between x and y

 [AU N/D 2008] [A.U CBT M/J 2010, CBT N/D 2011, CBT A/M 2011] [A.U A/M 2015 (RP) R13] [A.U M/J 2015 R13 PQT] [A.U M/J 2016 R13 RP] Solution: (i) Since both the lines of regression passes through the mean values must satisfy the two given regression lines

Since both the regression coefficients are positive r must be positive r = 0.6.

Example 3.3.3

The following table gives according to age x, the frequency of marks obtained '' by 100 students in an intelligence test. Measure the degree of relationship between age and intelligence test.

Example 3.3.4

Calculate the co-efficient of correlation between x and y from the following table and write down the regression equation of y on x : [AU. A/M. 2004]

Example 2.3.5

For the following data find the most likely price at Madras corresponding to the price 70 at Bombay and that at Bombay corresponding to the price 68 at Madras.

S.D. of the difference between the price at Madras & Bombay is 3.1 ? [A.U. A/M. 2004] [A.U N/D 2017 R-08]

Solution: Let X denote the price at Madras and Y denotes the price at Bombay.

Corresponding to the price 68 at Madras, the most likely price at Bombay is 84.43.

Similarly the line of regression of x on y is

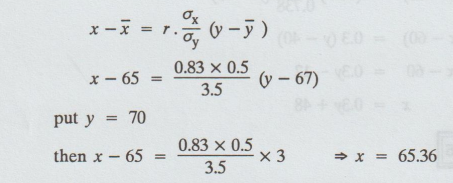
Corresponding to the price 70 at Bombay, the most likely price at Madras is 65.36.

Example 2.3.6

The regression equation of X on Y is 3Y-5X + 108 = 0. If the mean value of Y is 44 and the variance of X is (9/16)th of the variance of Y. Find the mean value of X and the correlation co-efficient.  [A.U A/M 2011]

Solution:

Example 2.3.7

The regression equations are 3x + 2y = 26 and 6x + y = 31. Find the correlation coefficient between X and Y.

[A.U N/D 2011]

[A.U N/D 2017 (RP) R-13] [A.U A/M 2019 (R17) PS}

Solution :

Example 2.3.8

The equations of two regression lines are 3x + 12y = 19 and 3y+9x = 46. Find   and the Correlation Coefficient between X and Y.  [A.U M/J 2013] [A.U N/D 2015 R13 PQT]

Solution: Since both the lines of regression passes through the mean values   must satisfy the two given regression lines