Regression

REGRESSION

(1) Regression

Regression is a mathematical measure of the average relationship between two or more variables in terms of the original limits of the data.

(2) Lines of regression

(1) The line of regression of y on x is given byd eigns or ai 0 11

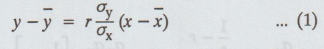
 (2) The line of regression of x on y is given by

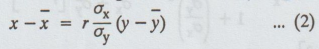
Note: Both the lines of regression passes through

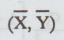
(3) Regression coefficients

 (1) Regression coefficient of y on x is r σ_y / σ_x = b_yx

 (2) Regression coefficient of x on y is r σ_x / σ_y = b_xy

Correlation coefficient r = ± √ b_yx b_xy

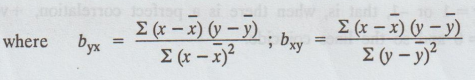
 (4) Properties of Regression Lines

 (1) The regression lines pass through  So  is the point of intersection of the regression lines.

(2) When r = 1, that is when there is a perfect +ve correlation or when r = -1, that is when there is a perfect -ve correlation the equation (1) and (2) becomes one are the same and so the regression lines coincide

 (3) When r = 0 the equations of the lines are  and which represent perpendicular lines which are parallel to the axis.

 (4) The slopes of the lines are r = σ_y / σ_x , 1 σ_y / r σ_x

Since the S.D's σ_x and σ_y are +ve, both the slopes are +ve if r is +ve and -ve if r is -ve. That is all the three, namely the two slopes and r are of same sign.

(5) Angle between the regression lines

The slopes of the regression lines are

m₁ = r σ_y / σ_x , m₂ = 1/r σ_y / σ_x ,

If θ is the angle between the lines, then

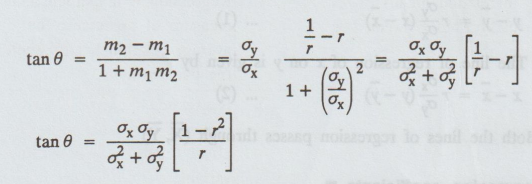
When will the two regression lines be (a) at right angles (b) Coincidert? [A.U N/D 2012] [A.U A/M 2019 (R13) PQT]

Note: 1. When r = 0, that is, there is no correlation between x and y.

tan θ = ∞ (or) θ = π/2 and so the regression lines are perpendicular

2. When r = 1 or -1, that is, when there is a perfect correlation, +ve or -ve, θ = 0 and so the lines coincide.

6. Correlation coefficient is the geometric between the two regression coefficients

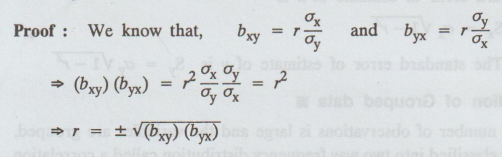
7. If one of the regression coefficient is greater than unity the other must be less than unity.

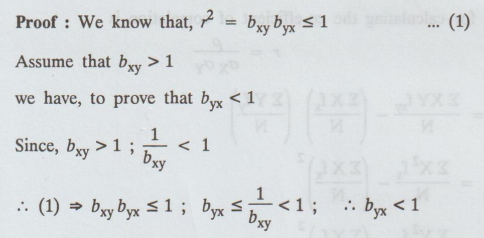
8. Distinguisg between correlation and regression Analysis

9. Standard errors of estimate

The standard error of estimate of x is

(1) S_x = σ_x, √1 - r²

 (2) The standard error of estimate of y is S_y = σ_xy√1 − r²

10. Correlation of Grouped data

When the number of observations is large and the variables are grouped, the data can be classified into two way frequency distribution called a correlation table. If there are 'n' classes for X and 'm' classes for Y, there will be (m × n) cells in the two-way table.

The formula for calculating the co-efficient of correlation is

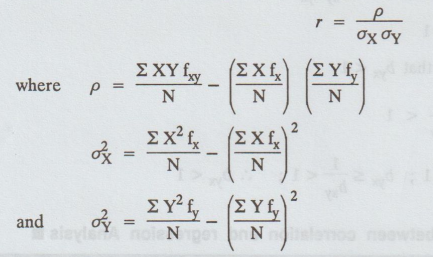
11. Probable Error of correlation co-efficient

The probable error of correlation co-efficient is given by,

P.E. (r) = 0.6745 × S.E.

where S.E. is the standard error and is S.E. (r) = 1 - r² / √n where ‘r’ is the correlation co-efficient and 'n' is the number of observation.

Thus P.E. (r) = 0.6745 (1 - r²) / √n

The reason for taking the factor 0.6745 is that in a normal distribution, the range μ = ± 0.6745 covers 50% of the total area. This error enables us to find the limits within which correlation co-efficient can be expected to vary.