Representation of Binary Tree

Representation of Binary Tree

There are two ways of representing the binary tree.

1. Sequential representation

2. Linked representation.

Let us see these representations one by one.

 

1. Sequential representation of binary trees or array representation :

Each node is sequentially arranged from top to bottom and from left to right. Let us understand this matter by numbering each node. The numbering will start from root node and then remaining nodes will give ever increasing numbers in level wise direction. The nodes on the same level will be numbered from left to right. The numbering will be as shown below.

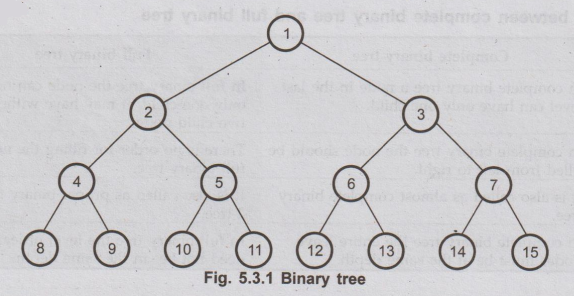
Now, observe Fig. 5.3.1 carefully. You will get a point that a binary tree of depth n having 2n-1 number of nodes. In Fig. 5.3.1 the tree is having the depth 4 and total number of nodes are 15. Thus remember that in a binary tree of depth n there will be maximum 2n-1 nodes. And so if we know the maximum depth of the tree then we can represent binary tree using arrays data structure. Because we can then predict the maximum size of an array that can accommodate the tree.

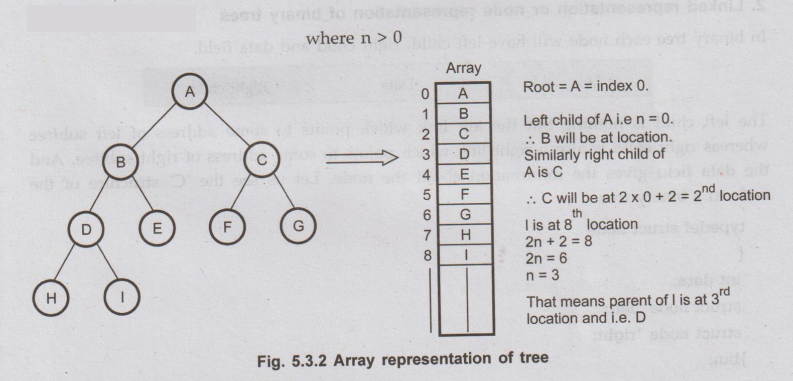
Thus array size can be > = n. The root will be at index 0. Its left child will be at index 1, its right child will be at index 2 and so on. Another way of placing the elements in the array is by applying the formula as shown below -

• When n = 0 the root node will placed at 0^th location

• Parent(n) = floor(n-1)/2

• Left(n) = (2n+1)

• Right(n) = (2n+2).

Advantages of sequential representation

The only advantage with this type of representation is that the direct access to any node can be possible and finding the parent, left or right children of any particular node is fast because of the random access.

Disadvantages of sequential representation

1. The major disadvantage with this type of representation is wastage of memory.

For example In the skewed tree half of the array is unutilized. You can easily understand this point simply by seeing Fig. 5.3.3.

2. In this type of representation the maximum depth of the tree has to be fixed because we have already decided the array size. If we choose the array size quite larger than the depth of the tree, then it will be wastage o of the memory. And if we choose array size lesser than the depth of the tree then we will be unable to represent some part of the tree.

3. The insertions and deletion of any node in the tree will be costlier as other nodes have to be adjusted at appropriate positions so that the meaning of binary tree can be preserved.

As these drawbacks are there with this sequential type of representation, we will search for more flexible representation. So instead of array we will make use of linked list to represent the tree.

 

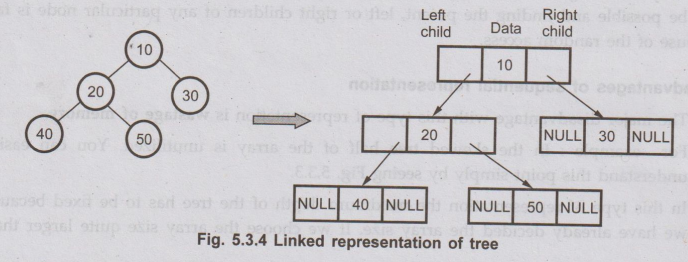
2. Linked representation or node representation of binary trees

In binary tree each node will have left child, right child and data field.

Left child   Data    Right child

The left child is nothing but the left link which points to some address of left subtree whereas right child is also a right link which points to some address of right subtree. And the data field gives the information about the node. Let us see the 'C' structure of the node in a binary tree.

typedef struct node

{

int data;

struct node *left;

struct node *right;

}bin;

The tree with Linked representation is as shown below-

Advantages of linked representation

1. This representation is superior to our array representation as there is no wastage of memory. And so there is no need to have prior knowledge of depth of the tree. Using dynamic memory concept one can create as many memory (nodes) as required. By chance if some nodes are unutilized one can delete the nodes by making the address free.

2. Insertions and deletions which are the most common operations can be done without moving the other nodes.

Disadvantages of linked representation

1. This representation does not provide direct access to a node and special algorithms are required.

2. This representation needs additional space in each node for storing the left and right sub-trees.

 

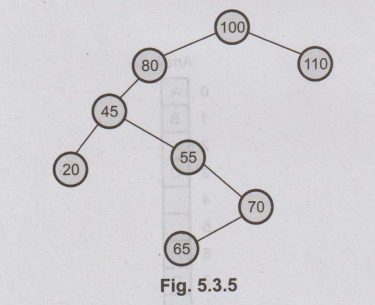
Ex. 5.3.1: For the given data draw a binary tree and show the array representation of the same: 100  80  45  55  110  20  70  65

Sol. The binary tree will be

Formula used for placing the node values in array are

1. Root will be at 0^th location

2. Parent(n) - floor (n - 1)/2

3. Left (n) = (2n+1)

4. Right (n) = (2n + 2)

where n > 0.

 

Ex. 5.3.2: What is binary tree? Show the array representation and linked representation for the following binary tree.

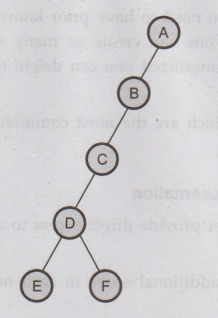
Sol. Binary Tree : Binary Tree is a finite set of nodes which is either empty or consists of a root and two disjoint binary trees called left subtree and right subtree.

Array Representation

Linked Representation