Retardation Test or Running Down Test

Retardation Test or Running Down Test

AU: Dec.-09, 15

•  This method is generally employed to shunt generators and shunt motors. From this method we can get stray losses. Thus if armature and shunt copper losses at any given load current are known then efficiency of a machine can be easily estimated.

 • The connections required for conducting this test are shown in the Fig. 5.7.1.

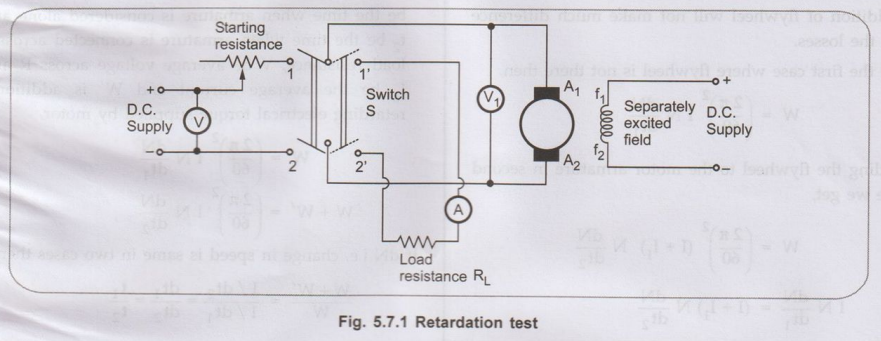
The machine whose test is to be taken is run at a speed which is slightly above its normal speed. The supply to the motor is cut off while the field is kept excited. The armature consequently slows down and its kinetic energy is used in supplying the rotational or stray losses which includes iron, friction and winding loss.

• If I is the moment of inertia of the armature and w is the angular velocity.

Kinetic energy of armature = ½ I ω²

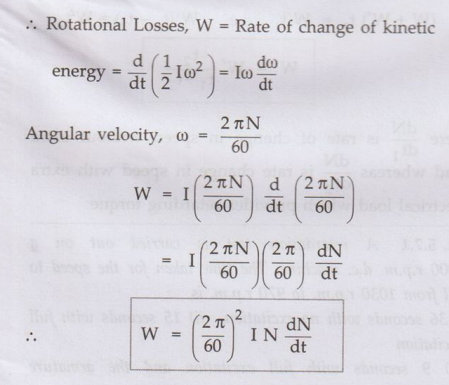
Thus if we want to find the rotational losses, the moment of inertia I and dN / dt must be known.

These quantities can be found as follows:

1. Determination of dN / dt

• The voltmeter V₁ which is connected across the armature will read the back e.m.f. of the motor. We know that back e.m.f. is proportional to speed so that voltmeter is calibrated to read the speed directly.

• When motor is cut-off from the supply, the speed decreases. The time required for definite decrease in speed is noted with the help of stop watch. A curve showing variation between time and speed which is obtained from voltmeter which is suitably calibrated is shown in the Fig. 5.7.2.

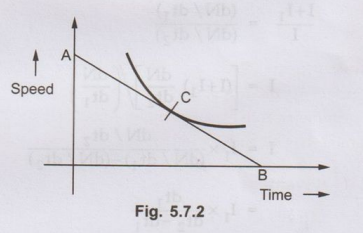
• At any point C corresponding to normal speed, a tangent AB is drawn. Then

dN /dt = OA (in r. p.m.) / OB (in seconds)

• The value obtained from above can be substituted in the expression for W which can give the rotational losses.

2. Determination of Moment of Inertia (I)

Method (a) - Using Flywheel

• The armature supply is cut off and time required for definite change in speed is noted to draw the corresponding curve as we have drawn in previous case. This curve is drawn considering only armature of the machine. Now a flywheel with known moment of inertia say I₁ is keyed onto the shaft and the same curve is drawn again. The slowing down time will be extended as combined moment of inertia of the two is increased.

• For any given speed (dN/dt₁) and (dN/dt₂) are determined same as previous case. It can be seen that the losses in both the cases are almost same as addition of flywheel will not make much difference to the losses.

• In the first case where flywheel is not there then,

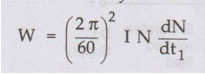
Adding the flywheel to the motor armature in second case we get,

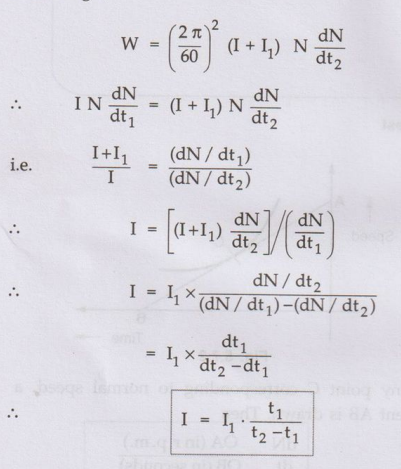
Method (b) - Without Using Flywheel

• In this method time is noted for the machine to slow down by say 5 % considering the armature alone. Then a retarding torque either mechanical or electrical is applied. Preferably electrical retarding torque is applied and time required to slow down by 5% is noted again. The method by which electrical torque can be provided is shown in the Fig. 5.7.1 in which the switch S after disconnecting from the supply is thrown to terminals 1'2'. The machine then gets connected to a non-inductive load resistance R_L. The power drawn by this resistance will acts as a retarding torque on the armature which will make it slow more quickly.

• The additional loss in the resistance will be equal to product of ammeter reading and the average reading of the voltmeter (for a fall of 5 % of voltmeter reading, the time is noted.) The ammeter reading is also changing so its average reading is taken. Thus the additional loss is I_a² (R_a + R). Let t₁ be the time when armature is considered alone and t₂ be the time when armature is connected across a load resistance, V be average voltage across R and I be the average current and W' is additional retarding electrical torque supplied by motor.

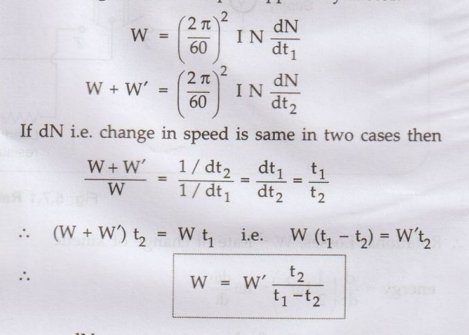
Here dN / dt₁ is rate of change in speed without extra load whereas dN / dt₂ is rate change in speed with extra dt2 electrical load which provides retarding torque.

Ex. 5.7.1 A retardation test is carried out on 1000 r.p.m. d.c. machine. The time taken for the speed to fall from 1030 r.p.m. to 970 r.p.m. is

i) 36 seconds with no excitation. ii) 15 seconds with full excitation

iii) 9 seconds with full excitation and the armature supporting an extra load of 10 A at 219 V.

Calculate: 1) The moment of inertia of the armature in kg.m². 2) Iron loss.

3) Mechanical loss at the mean speed of 1000 r.p.m.

Sol. : Remember that,

1. When armature is slowing down and there is no excitation, then kinetic energy is used to overcome mechanical losses only. Iron losses are absent as excitation is absent.

2. When excitation is given, kinetic energy is used to overcome both mechanical as well as iron losses. Total called stray losses.

3. If moment of inertia is in kg-m², then loss of energy is in watts.

The mechanical losses are,

Ex. 5.7.2 A retardation test made on a separately-excited d.c. machine as a motor. The induced voltage falls from 240 V to 225 V in 25 seconds on opening the armature circuit and 6 seconds on suddenly changing the armature connection from supply to a load resistance taking 10 A (average). Find the efficiency of the machine when running as a motor and taking a current of 25 A on a supply of 250 V. The resistance of its armature is 0.4 Ω and that of its field wi nding is 250 Ω. AU: Dec.-09, Marks 8

Sol. :Average voltage across the load

Review Questions

1. Describe the retardation test as applied to the d.c. shunt machines.

AU: Dec.-15, Marks 8

2. How can stray losses of machine be determined with the help of a retardation test with and without the knowledge of moment of inertia ?

3. A retardation test is made on a separately excited d.c. machine as a motor. The induced voltage falls from 240 V to 220 V in 25 seconds on opening the armature circuit and in 6 seconds on suddenly changing the armature connection from supply to a load resistance which takes average current of 10 A. Find the efficiency of the machine when running as a motor taking a current of 25 A on a supply of 250 V. The resistance of its armature is 0.3Ω and that of its field winding is 200 Ω. (Ans.: 80.67%)

4. A retardation test is carried out on a 1000 r.p.m. d.c. machine. The time taken for the speed to fall from 1030 r.p.m. to 970 r.p.m. is,

a) 40 seconds with no excitation b) 20 seconds with full excitation c) 9 seconds with full excitation and the armature supplying an extra load of 10 A at 225 V.

Calculate i) The moment of inertia of the armature in kg-m² ii) Iron losses iii) The mechanical losses at the mean speed of 1000 r.p.m.

(Ans. : 55.95 kg-m², 920.45 watts, 920.45 watts)