Ring Counters

Ring Counters

• Fig. 6.6.1 shows the logic diagram for four-bit ring counter.

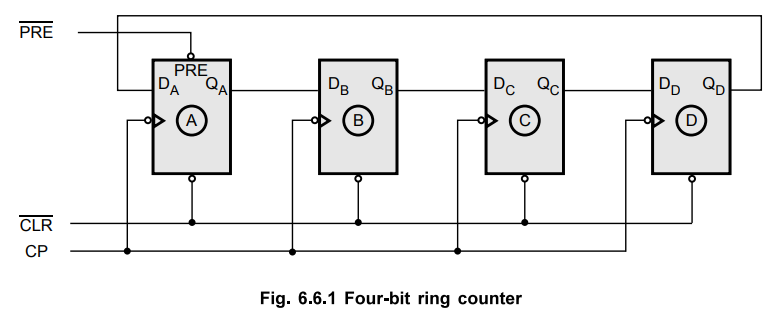
• The Q output of each stage is connected to the D input of the next stage and the output of last stage is fed back to the input of first stage.

• The  followed by  makes the output of first stage to 'I' and remaining outputs are zero, i.e. Q_A is one and Q_B, Q_C, Q_D are zero.

• The first clock pulse produces QB = 1 and remaining outputs are zero.

• According to the clock pulses applied at the clock input CP, a sequence of four states is produced. These states are listed in Table 6.6.1.

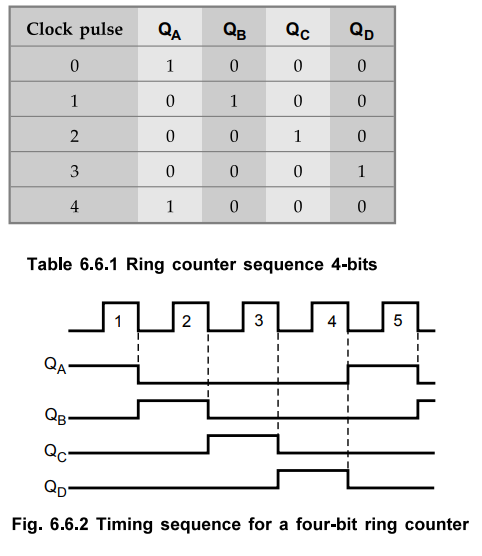
• 1 is always retained in the counter and simply shifted 'around the ring', advancing one stage for each clock pulse. In this case four stages of flip-flops are used. So a sequence of four states is produced and repeated.

• Fig. 6.6.1 gives the timing sequence for a four-bit ring counter.

• The ring counter can be used for counting the number of pulses.

• The number of pulses counted is read by noting which flip-flop is in state 1.

• No decoding circuitry is required.

• Since there is one pulse at the output for each of the N clock pulses, this circuit is also referred to as a divide-by-N-counter or an N : 1 scalar.

• Ring counters can be instructed for any desired MOD number, that is MOD-N ring counter requires N flip-flops.

Ex. 6.6.1 Draw a six stage ring counter and explain its operation. Mention about the use of presetting the counter.

AU : CSE : Dec.-05, Marks 16

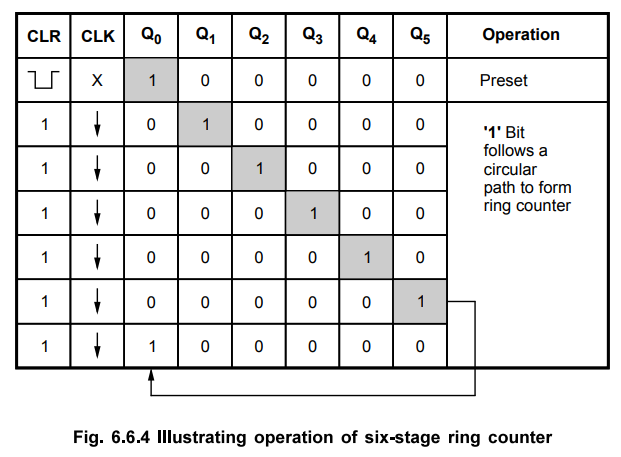
Sol. : The Fig. 6.6.3 shows the six stage ring counter. The counter is present to value (000001)₂ by setting bit 0 = 1 and remaining bits = 0.

Operation : The Fig. 6.6.4 shows the operation of six-stage ring counter. On preset, FFO (flip-flop 0) is set and FF1 to FF5 are reset. After each falling edge of the clock contents of ring counter are shifted 1 bit from LSB to MSB.

Review Questions

1. Draw a six stage ring counter and explain its operation.

AU CSE Dec.-05, Marks 16

2. Draw the timing diagram of 4-bit ring counter.

AU CSE Dec.-04, Marks 2

3. Draw a 2-bit ripple counter and convert this into a 2-bit ring counter.

AU CSE Dec.-05, Marks 2