Scalar or Dot Product of Vectors

Scalar or Dot Product of Vectors

AU : May-06, Dec.-09

• The scalar or dot of the two vectors 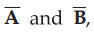 is denoted as and defined as the product of the magnitude of A, the magnitude of B and the cosine of the smaller angle between them.

• It also can be defined as the product of magnitude of  and the projection of   onto  or viceversa.

• Mathematically it is expressed as,

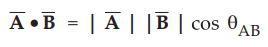 ... (1.10.1)

• The result of such a dot product is scalar hence it is also called scalar product.

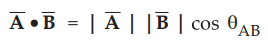
1. Properties of Dot Product

• The various properties of the dot product are,

1. If the two vectors are parallel to each other i.e. θ = 0° then cos θ_AB = 1 thus

 for parallel vectors         ... (1.10.2)

2. If the two vectors are perpendicular to each other i.e. θ = 90° then cos θ_AB = 0 thus

 = 0 for perpendicular vectors        ... (1.10.3)

• In other words, if dot product of the two vectors is zero, the two vectors are perpendicular to each other.

3. The dot product obeys commutative law,

   ...(1.10.4)

4. The dot product obeys distributive law,

    ...(1.10.5)

5. If the dot product of vector with itself is performed, the result is square of the magnitude of that vector.

 ...(1.10.6)

6. Consider the unit vectors 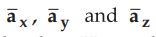 in cartesian co-ordinate system. All these vectors are mutually perpendicular to each other. Hence the dot product of different unit vectors is zero.

... (1.10.7)

7. Any unit vector dotted with itself is unity,

 ... (1.10.8)

8. Consider two vectors in cartesian co-ordinate system,

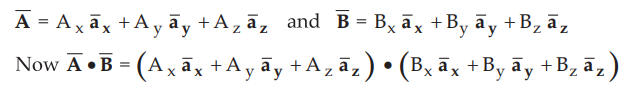
• This product has nine scalar terms as dot product obeys distributive law. But from the equation (1.10.7), six terms out of nine will be zero involving the dot products of different unit vectors. While the remaining three terms involve the unit vector dotted with itself, the result of which is unity.

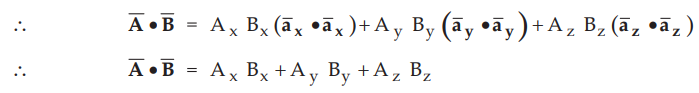... (1.10.9)

2. Applications of Dot Product

The applications of dot product are,

1. To determine the angle between the two vectors.

The angle can be determined as,

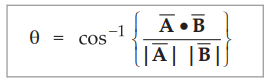
2. To find the component of a vector in a given direction.

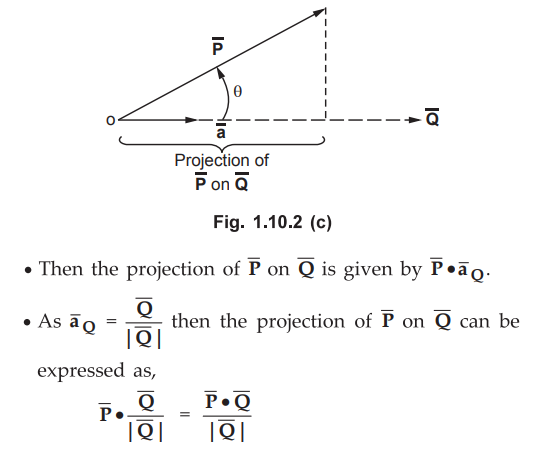
• Consider a vector  as shown in the Fig. 1.10.2 (a). The component of vector  in the direction of unit vector a is 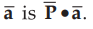. This is a scalar quantity. This is shown in the Fig. 1.10.2 (a).

p

• The sign of this component is positive if 0 ≤ θ < 90^o while the sign of this component is negative if 90^o < θ ≤180^o . If the component vector of p  in the direction of unit vector  is required then multiply the component obtained by that unit vector, as shown in the Fig. 1.10.2 (b). Thus  is the component vector of  

• This is the geometrical meaning of dot product, to find projection of  in the direction of unit vector

• If the projection of on other vector  is to be obtained then it is necessary to find unit vector in the direction of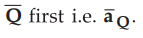 

3 Physically, work done by a constant force can be expressed as a dot product of two vectors.

• Consider a constant force  acting on a body and it causes the displacement  of that body. Then the work done W is the product of the force and the component of the displacement in the direction of force which can be expressed as,

• But if the force applied varies along the path then the total work done is to be calculated by the integration of a dot product as,

Examples for Practice

Review Question

1. Define dot product of vectors. State its applications.