Second Order Low Pass Butterworth Filter using Op-amp

Second Order Low Pass Butterworth Filter

April-02, May-06, 07, 09, 11, 17, Dec.-03, 11, 15, 17

The practical response of the filter must be very close to an ideal one. In case of low pass filter, it is always desirable that the gain rolls off very fast after the cut off frequency, in the stop band. In case of first order filter, it rolls off at a rate of 20dB/decade. In case of second order filter, the gain rolls off at a rate of 40 dB/decade. Thus, the slope of the frequency response after f = f_H is -40 dB/decade, for a second order low pass filter.

A first order filter can be converted to second order type by using an additional RC network as shown in the Fig. 3.7.1.

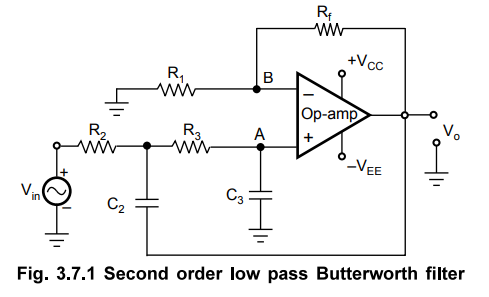
The cut off frequency fH for the filter is now decided by R₂, C₂, R₃ and C₃. The gain of the filter is as usual decided by op-amp i.e. the resistance R₁ and R_f.   

1. Analysis of the Filter Circuit

For deriving the expression for the cut off frequency, let us use the Laplace transform method.

The input RC network can be represented in the Laplace domain as shown in Fig. 3.7.2.

Now

As the order of s in the gain expression is two, the filter is called second order filter. The standard form of the transfer function of any second order system is

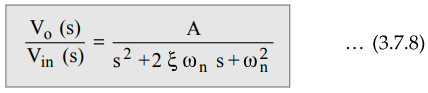
where A = Overall gain, ᶓ = Damping of system, ω_n - Natural frequency of oscillations

Comparing equation (3.7.7) and equation (3.7.8), we can say that

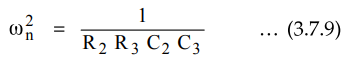
In case of filters, this frequency is nothing but the cut-off frequency, ω_H

This is the required cut off frequency .... (3.7.10)

Replacing s by jω, the transfer function can be written in the frequency domain and hence, finally, can be expressed in the polar form as,

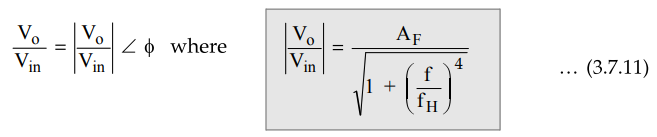
and    A_F = Gain of filter in pass band , f - Input frequency in Hz

f_H = High cut-off frequency in Hz

The frequency response is shown in Fig. 3.7.3.

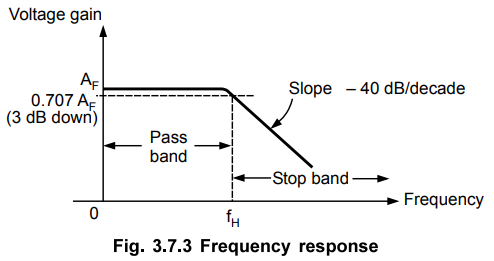
At the cut-off frequency, fH' the gain is 0.707 AF i.e. 3 dB down from its 0 Hz level. After, f_H(f > f_H), the gain rolls off at a rate of 40 dB/decade. Hence, the slope of the response after fH is - 40 dB/decade. 

2. Design Steps

The design steps for second order low pass Butterworth filter are

1) Choose the cut-off frequency f_H.

2) The design can be simplified by selecting R₂ = R₃ = R and C₂ = C₃ = C.

And choose a value of C less than or equal to 1 µF.

3) Calculate the value of R from the equation,

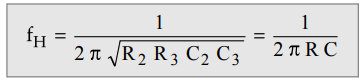
4) As R₂ = R₃ = R and C₂ = C₃ = C, the pass band voltage gain A_F = (1 + R_f/R₁) of the second order low pass filter has to be equal to 1.586.

Note For R₂ = R₃ = R and C₂ = C₃ = C, the transfer function takes the form.

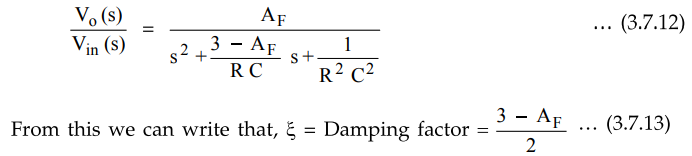
Now, for second order Butterworth filter, the middle term required is √2 = 1.414, from the normalised Butterworth polynomial.

3 - A_F = √2 = 1.414  i.e A_F = 1.586  …. (3.7.14)

Thus, to ensure the Butterworth response, it is necessary that the gain A_F is 1.586.

Key Point Hence, choose a value of R₁ ≤ 100 kΩ and calculate the corresponding value of R_f

The frequency scaling method discussed earlier for first order filter is equally applicable to the second order filter.

Example 3.7.1 Design a second order Butterworth low pass filter having upper cut-off frequency of 1 kHz.

Solution :

Step 1 : f_H = 1 kHz

Step 2 : Choose C₂ = C₃ = C = 0.01 µF 

Step 3 : Choose R₂ = R₃ = R

f_H = 1 / 2πRC  i.e. R = 15.915 kΩ

Step 4 : For Butterworth response,

R_f = 0.586 R1

Choose R₁ = 10 kΩ

R_f = 5.86 kΩ

Use a 10 kΩ potentiometer for precise adjustment of R_f.

The designed circuit is shown in the Fig. 3.7.4.

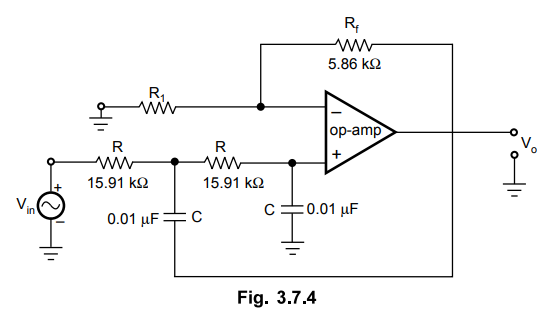
Example 3.7.2 Design a second order Butterworth low pass filter with cut off frequency 2 kHz.

May-17, Marks 6

Solution : Refer Ex. 3.7.1 for the procedure and verify the component values as,

C = 0.01 µF, R = 7.95 kΩ , R₁ = 10 kΩ, R_f = 5.86 kΩ.

Review Question

1. Draw the circuit diagram of a second order Butterworth active low pass filter and derive an expression for its transfer function.