Self Induced E.M.F.

Self Induced E.M.F.

AU : Dec.-06,10,12, May-17

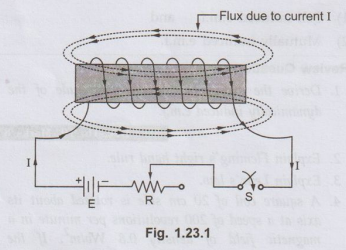
• Consider a coil having 'N' turns and carrying current T when switch 'S' is in closed position. The current magnitude can be varied with the help of variable resistance connected in series with battery, coil and switch as shown in the Fig. 1.23.1

• The flux produced by the coil links with the coil itself. The total flux linkages of coil will be N 0 Wb-turns. Now if the current 'I' is changed with the help of variable resistance, then flux produced will also change, due to which flux linkages will also change.

 • Hence according to Faraday's law, due to rate of change of flux linkages there will be induced e.m.f. in the coil. So without physically moving coil or flux there is induced e.m.f. in the coil. The phenomenon is called self induction.

• The e.m.f. induced in a coil due to the change of its own flux linked with it is called self induced e.m.f.

Key Point : The self induced e.m.f. lasts till the current in the coil is changing. The direction of such induced e.m.f. can be obtained by Lenz's law.

1. Self Inductance

• According to Lenz's law the direction of this induced e.m.f. will be so as to oppose the cause producing it. The cause is the current I hence the self induced e.m.f. will try to set up a current which is in opposite direction to that of current I. When current is increased, self induced e.m.f. reduces the current tries to keep it to its original value. If current is decreased, self induced e.m.f. increases the current and tries to maintain it back to its original value. So any change in current through coil is opposed by the coil

• This property of the coil which opposes any change in the current passing through it is called Self Inductance or Only Inductance.

• It is analogous to electrical inertia or electromagnetic inertia.

2. Magnitude of Self Induced E.M.F.

From the Faraday's law of electromagnetic induction, self induced e.m.f. can be expressed as   

e = - N dϕ/dt

Negative sign indicates that direction of this e.m.f. is opposing change in current due to which it exists.

The flux can be expressed as,

ϕ = ( Flux / Ampere )× Ampere = ϕ/I  × I

Now for a circuit, as long as permeability 'µ' is constant, ratio of flux to current (i.e. B/H) remains constant.

ஃ  Rate of change of flux = ϕ/I × Rate of change of current

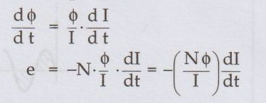
 The constant Nϕ/I  in this expression is nothing but the quantitative measure of the property due to which coil opposes any change in current.

So this constant Nϕ/I  is called coefficient of self inductance and denoted by 'L'.

ஃ L = Nϕ/I

It can be defined as flux linkages per ampere current in it. Its unit is henry (H).

 A circuit possesses a self inductance of 1 H when a current of 1 A through it produces flux linkages of 1 Wb-turn in it.

ஃ e  = -L dI/dt volts

From this equation , the unit henry of self inductance can be defined as below.

Key Point : A circuit possesses an inductance of 1 H when a current through coil is changing uniformly at the rate of one ampere per second inducing an opposing e.m.f. 1 volt in it.

• The coefficient of self inductance is also defined as the e.m.f. induced in volts when the current in the circuit changes uniformly at the rate of one ampere per second.

3. Expressions for Coefficient of Self Inductance (L)

Ex. 1.23.1 If a coil has 500 turns is linked with a flux of 50 mWb, when carrying a current of 125 A. Calculate the inductance of the coil. If this current is reduced to zero uniformly in 0.1 sec, calculate the self induced e.m.f. in the coil.

Sol. : The inductance is given by,

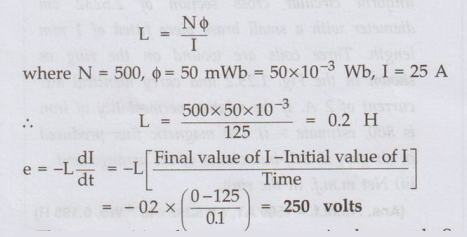
• This is positive because current is decreased. So this 'e' will try to oppose this decrease, means will try to increase current and will help the growth of the current

Ex. 1.23.2 A coil is wound uniformly on an iron core. The relative permeability of the iron is 1400. The length of the magnetic circuit is 70 cm. The cross-sectional area of the core is 5 cm². The coil has 1000 turns. Calculate, 

i) Reluctance of magnetic circuit

ii) Inductance of coil in henries.

iii) E.M.F. induced in coil if a current of 10 A is reversed in 0.2 seconds.

 Sol. :

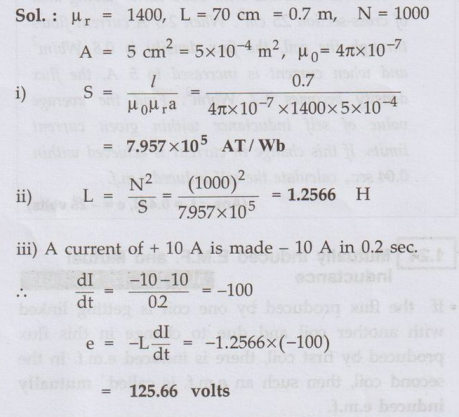
Again it is positive indicating that this e.m.f. opposes the reversal i.e. decrease of current from +10 towards -10 A.

Review Questions

1. Define inductance of a coil. AU : Dec.-10, Marks 4    

2. Derive the various expressions for the self inductance. AU : Dec.-12, May-17, Marks 4

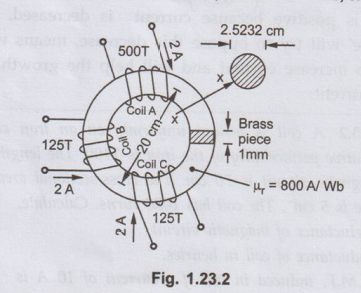
3. An iron ring has a mean diameter of 20 cm and a uniform circular cross section of 2.5232 cm diameter with a small brass piece fitted of 1 mm length. Three coils are wound on the ring as shown in the Fig. 1.29.2 and carry identical d.c. current of 2 A. If the relative permeability of iron is 800, estimate :- i) The magnetic flux produced in air-gap, ii) Self-inductance of the arrangement. iii) Net m.m.f. in the ring. 

(Ans. : m.m.f. = 1500 AT, O = 5.282 x 10-4 Wb. 0.198 H)

4. A solenoid is wound with 1000 turns having area of cross-section 25 cm². When 2.5 A current flows through the coil, the flux density is 0.8 Wb/m² and when current is increased to 5 A, the flux density becomes 1.2 Wb/m². Find the average value of self inductance within given current limits. If this change in current is achieved within 0.04 sec., calculate the self induced e.m.f. 

(Ans. : L = 0.4 H, e = - 25 volts)