Series Combination of Resistors

COMBINATION OF RESISTORS

In a practical case we may have many resistors. We have to connect them for getting desired resistance. The resistors can be connected in the following three fashions.

(a) Series combination

(b) Parallel combination

(c) Series - parallel combination

Series Combination

If the resistors are connected end to end, the combination is said to be series. The voltage source (energy source) is connected between the free ends. Refer the Fig. 1.7 (a). The resistors R₁, R₂ and R₃ are all connected end to end. The free terminals A and B are connected to the voltage source.

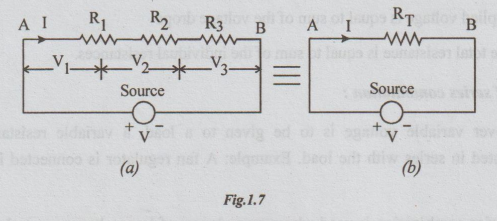
Since there is only one closed loop, only one current flows, i.e., the source current flows through all the elements. In other words if the current is same through all the resistors, the combination is called series combination.

There is a voltage drop across each resistor.

To find equivalent resistance:

Let V = applied voltage,

I = source current = current through each element

V₁, V₂, V₃ are the voltages across R₁, R₂ and R₃ respectively.

By ohms law V₁ = IR₁

V₂ = IR₂ and V₃ = IR₃

But V = V₁+ V₂+ V₃

= IR₁ + IR₂+ IR₃

= I (R₁ + R₂+ R₃)... (i)

If R_T be the equivalent resistance of the combination, its value should be such that the same current as above flows through it when applied voltage is same.

By ohm's law V = I × R_T  ....(ii)

From the equations (i) and (ii) we get

R_T = R₁ + R₂+ R₃

From the series combination the following salient points are to be remembered.

(i) In the series combination, the current is same through all the elements. In other words, if the current through the elements is same then the combination is series combination

(ii) The voltage is distributed. The voltage across the resistor is proportional to its resistance.

(iii) The equivalent resistant R_T (also known as total resistant R_T) is greater than the greatest individual resistance of that combination.

(iv) Powers are additive

(v) Applied voltage is equal to sum of the voltage drops

(vi) The total resistance is equal to sum of the individual resistances.

Applications of series combination:

1. Wherever variable voltage is to be given to a load, a variable resistance (rheostat) is connected in series with the load. Example: A fan regulator is connected in series with the fan.

2. The series combination is used where many lamps of low voltages are to be operated on the main supply. Example: Decoration lights.

3. When a load of low voltage is to be operated on a high voltage supply, a fixed value of resistance is connected in series with the load.

Disadvantage of series circuits:

(i) If any break takes place at any point in a circuit, there will not be any current flow. Hence the entire circuit becomes useless.

(ii) Suppose that there are two lamps each rated 230 Volts, 100 watts and let the supply voltage be 230 volts. If the two lamps are connected in series we require a total voltage of 2 × 230 = 460 volts for satisfactory operation. But the available voltage is only 230 volts. If the combination is series connected to 230 volts, the lamps will be operating with the dim light. It is not desirable. In each and every house, in India the single phase supply is only 230 volts. Hence series circuits is not practicable for lighting circuits.

(iii) Take examples of two Bulbs A and B. A rated 115 volts and 100 watts and B rated 115 volts, 50 watts. If these two are connected in series across a supply voltage of 230 volts, no damage will take place but operation cannot be with efficiency.

Note: 1. If there are n resistors each of value of R ohms in series the total resistance is given by R_T = n × R.

2. If there are two resistors R₁ and R₂ in series connected across a supply voltage of V,

V₁ = VR₁ / R₁ + R₂

And V₂ = VR₂ /R₁ + R₂

WORKED EXAMPLES ON SERIES RESISTIVE CIRCUITS

Example 1 The lamps in a set of Christmas tree lights are connected in series. If there are 20 lamps and each lamp has resistance of 25Ω, calculate the total resistance of the set of lamps and hence calculate the current taken from a supply of 230 volts.

Solution: Supply voltage = V = 230 volts

Resistance of each lamp R = 25 Ω

No. of lamps in series = n = 20

Total resistance RT = n R

= 20 × 25 = 500 Ω

Current from supply I = V/RT = 230 / 500 = 0.46 A

Example 2 The field coil of a d.c. generator has a resistance of 250 Ω and is supplied from a 220 V source. If the current in the field coil is to be limited to 0.44A, calculate the resistance of the resistor to be connected in series with the coil.

Solution:

Source voltage = V = 220 volts

Field coil resistance = Rf = 250 Ω

Let the resistance of the resistor in series with Rf be R Ω

Total resistance RT = Rf + R = 250+ R

Given that, Current I = 0.44 A

By Ohm's law RT = V/I

= 220/0.44 = 500

⇒ = 250+ R 500 Ω

R = 500-250 =250 Ω

Ans: R =250 Ω

Example 3 An incandescent lamp is rated for 110V, 100W. Using a suitable resistor how can you operate this lamp on 220 V mains.

Solution:

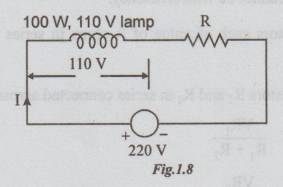
Rated current of the lamp I = power / voltage

= 100 / 110 = 10 / 11A

For satisfactory operation of the lamp, current of 10 / 11 A should flow.

When the voltage across lamp is 110V, then the remaining voltage must be across R.

Supply voltage V = 220 volts

Voltage across R = V - 110 volts

i.e.,VR = 220-110

= 110 V

By Ohm's law, VR = IR

⇒ 110 = 10/11 R

Ans: R = 121 Ω

Example 4 A 100 W, 250 V bulb is put in series with a 40W, 250 V bulb across a 500 V supply. What will be the current drawn? What will be the power consumed by each bulb? Will such a combination work?

Solution:

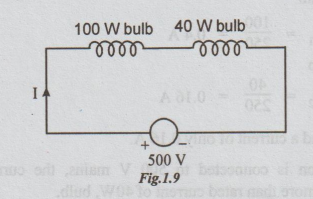
Resistance = (voltage)2 / power

Let R1 = Resistance of 100 W bulb

R2 = Resistance of 40 W bulb

From the details of rating

R1= (250)2/100 = 625 Ω

R2 = (250)2 /40 = 1562.5 Ω

When the bulbs are put in series

RT = R1 + R2

= 625+ 1562.5

= 2187.5 Ω

Voltage across the bulbs

V = 500 volts (given)

 Current I = V/RT

= 500 / 2187.5 = 0.2286 A

Power consumed by 100 W bulb

P1 = I2R1

= (0.2286)2 (625)

= 32.66 W

Power consumed by 40 W bulb

P2 = I2R2

= (0.2286)2 (1562.5)

= 81.7 W

When 40W bulb will try to draw a power of 81.63 W, its filament will be overheated and will burn. Hence such combination will not work.

Note: Another way of reasoning.

Rated current of 100 W bulb

I1  = 100/250== 0.4 A

Rated current of 40W bulb

I2 = 40/250 =0.16 A

That is, 40 W can withstand a current of only 0.16 A.

But when the combination is connected to 500 V mains, the current through the both bulbs theoretically is 0.2286A. It is more than rated current of 40W, bulb.

Due to this high current, the filament of 40W bulb gets overheated and will burn. It makes the circuit open.