Sine Wave Generators (Oscillators), Phase Shift Oscillator using Op-amp

Sine Wave Generators (Oscillators)

The sine wave is certainly one of the most fundamental waveforms. A variety of circuits and techniques have been developed for the generation of sine waves. The conventional sine wave oscillator circuits use phase shifting techniques that usually employ.

• Two RC tuning networks, and

• Complex amplitude limiting circuitry

Let us discuss the two commonly used oscillators for the sine wave generation. 

Phase Shift Oscillator

RC phase shift oscillator basically consists of an amplifier and a feedback network consisting of resistors and capacitors arranged in ladder fashion. Hence such an oscillator is also called ladder type RC phase shift oscillator.

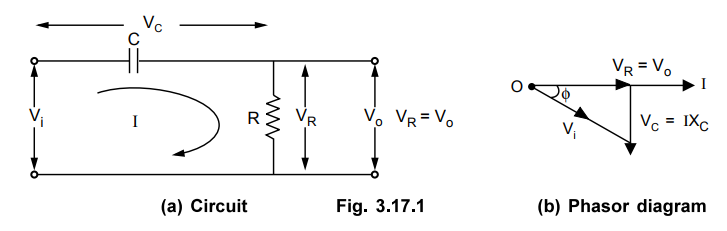
To understand the operation of this oscillator let us study RC circuit first, which is used in the feedback network of this oscillator. The Fig. 3.17.1 shows the basic RC circuit.

The capacitor C and resistance R are in series. Now X_C  is the capacitive reactance in ohms given by,

X_C = (1 / 2πfC) Ω

The total impedance of the circuit is,

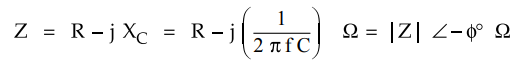
The r.m.s. value of the input voltage applied is say V4 volts. Hence the current is given by,

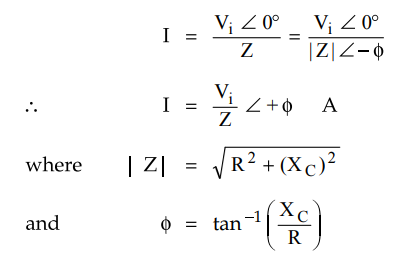
From expression of current it can be seen that current I leads input voltage V_i by angle ϕ. The output voltage Vo is the drop across resistance R given by,

V_o = V_R = IR 

The voltage across the capacitor is,

V_C = I X_C

The drop VR is in phase with current I while the drop V_C lags current I by 90° i.e. I leads V_C by 90°. The phasor diagram is shown in the Fig. 3.17.1 (b).

Key Point By using proper values of R and C, the angle 0 is adjusted in practice equal to 60°.

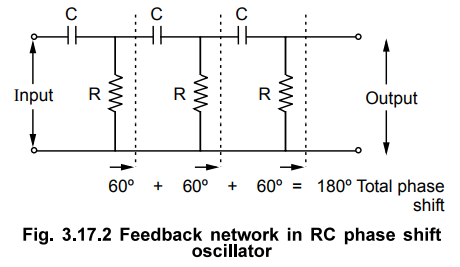
1. RC Feedback Network

As stated earlier, RC network is network must introduce a phase shift of 1809 to obtain total phase shift around a loop as 360°. Thus if one RC network produces phase shift of 0 = 6(F then to produce phase shift of 1809 such three RC networks must be connected in cascade. Hence in RC phase shift oscillator, the feedback network consists of three RC sections each producing a phase shift of 60°, thus total phase shift due to feedback is 180° (3 × 60°) Such a feedback network is shown in the Fig. 3.17.2.

The network is also called the ladder network. All the resistance values and all the capacitance values are same, so that for a particular frequency, each section of R and C produces a phase shift of 60°.

2. R-C Phase Shift Oscillator using Op-amp

R-C phase shift oscillator using op-amp uses op-amp in inverting amplifier mode. Thus it introduces the phase shift of 180” between input and output. The feedback network consists of 3 RC sections each producing 60° phase shift. Such a RC phase shift oscillator using op-amp is shown in the Fig. 3.17.3.

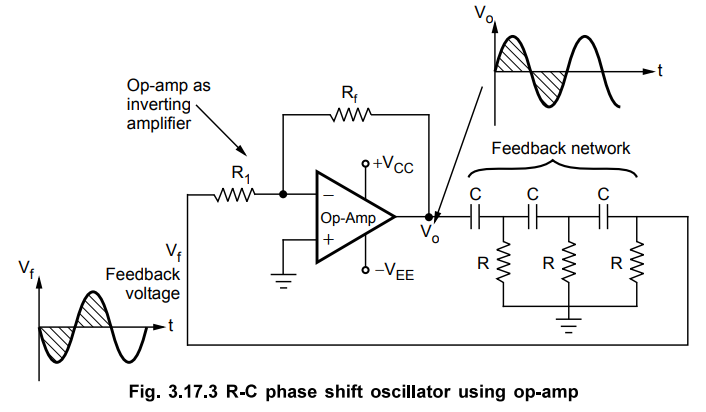
The output of amplifier is given to feedback network. The output of feedback network drives the amplifier. The total phase shift around a loop is 180° of amplifier and 1809 due to 3 RC section, thus 360°. This satisfies the required condition for positive feedback and circuit works as an oscillator.

3. Derivation of Frequency of Oscillations

Let us find the transfer function of the RC feedback network.

Applying KVL to various loops we get,

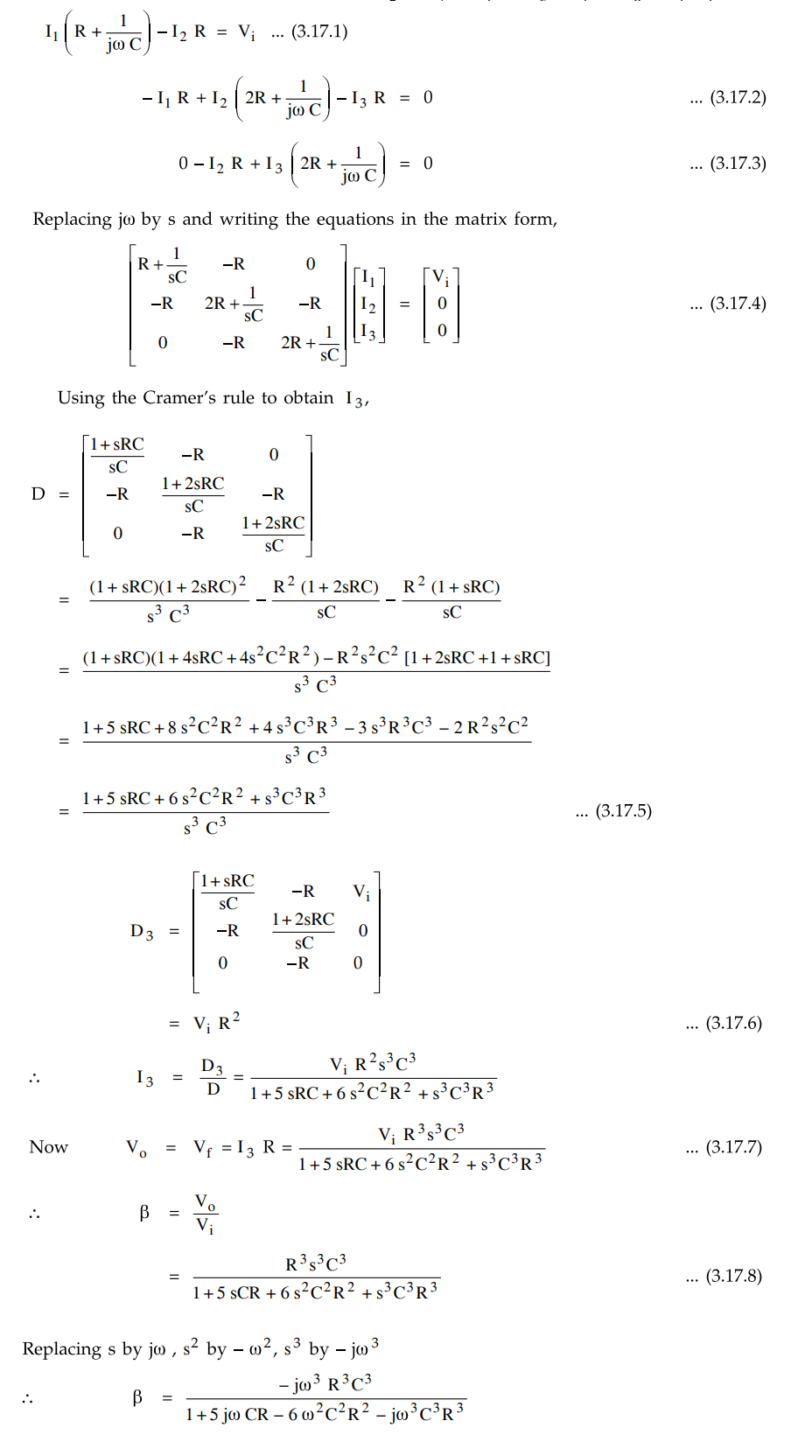
Dividing numerator and denominator by –jω³ R³ C³ and using,

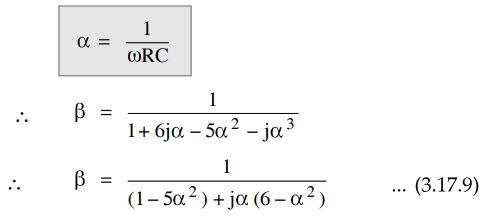
To have phase shift of 180°, the imaginary part in the denominator must be zero, a

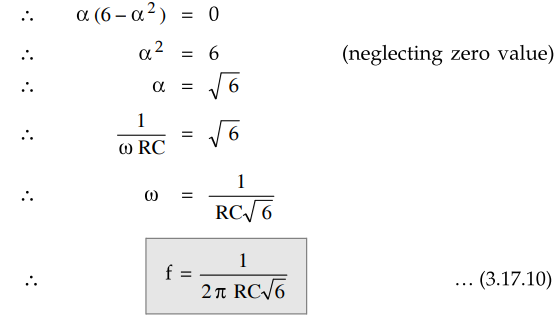
This is the frequency with which circuit oscillates.

At this frequency,

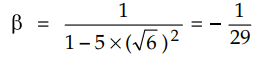
Negative sign indicates phase shift of 180°

Key Point For the oscillations to occur, the gain of the op-amp must he equal to or greater than 29, which can be adjusted using the resistances R_f and R_i.

4. Advantages

The advantages of R-C phase shift oscillator are,

1. The circuit is simple to design.

2. Can produce output over audio frequency range.

3. Produces sinusoidal output waveform.

4. It is a fixed frequency oscillator.

5. Disadvantage

By changing the values of R and C, the frequency of the oscillator can be changed. But the values of R and C of all three sections must be changed simultaneously to satisfy the oscillating conditions. But this is practically impossible. Hence the phase shift oscillator is considered as a fixed frequency oscillator, for all practical purposes.

And the frequency stability is poor due to the changes in the values of various components, due to effect of temperature, aging etc.

6. Phase Shift Oscillator Design

Practically the resistance R_f of the inverting amplifier is designed, by making current through it, much larger than input bias current of the op-amp.

Let the current through R_f is I₁ then

I₁ = 100 I_b (max)  … (3.17.13)

Without amplitude stabilization, the output of the oscillator oscillates between the levels ± V_sat.

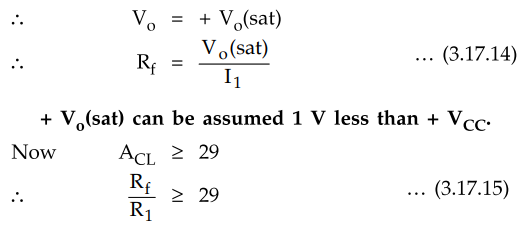
Design the value of R₁ from the gain requirement.

To prevent the loading of the amplifier because of RC networks, it is necessary that R₁ ≥ 10 R.

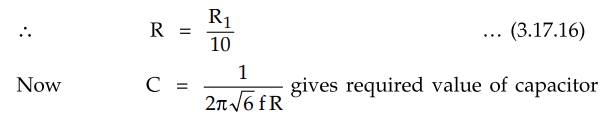
Note that for output frequency less than 1 kHz, op-amp 741 is used but for higher frequencies LM 318 or LF 351 op-amps are recommended due to their higher slew rates.

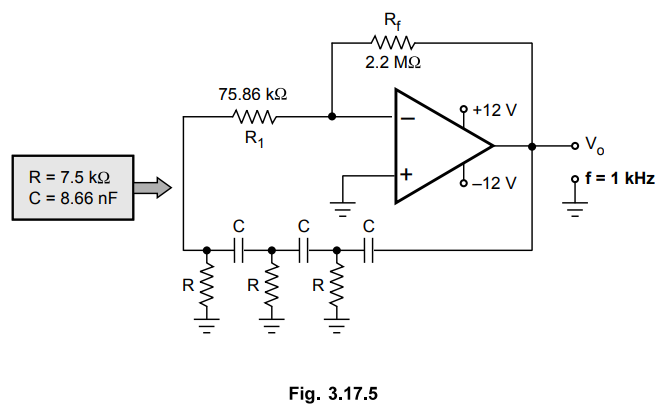
Example 3.17.1 Design a RC phase shift oscillator for a frequency of 1 kHz.

Dec.-04, 14, Marks 8

Solution : Use op-amp 741 with I_b (max) = 50 nA

The designed circuit is shown in the Fig. 3.17.5

Review Question

1. Draw the circuit of a RC phase shift oscillator using operational amplifier and derive an expression for the condition of oscillation, gain of op-amp and frequency of oscillation.

Dec.-04, 12, May-05, 12, Marks 16