Single Tuned Amplifiers

Single Tuned Amplifiers

AU : Dec.-04, 05, 06, 07, 08, 09, 10, 11, 12, 15 May-03,04, 05, 06, 07, 09, 11, 12, 13

1. Introduction

• To amplify the selective range of frequencies, the resistive load, Rc is replaced by a tuned circuit. The tuned circuit is capable of amplifying a signal over a narrow band of frequencies centered at fr. The amplifiers with such a tuned circuit as a load are known as tuned amplifier. Since tuned amplifiers amplify narrow band of frequencies they are also known as narrow band amplifiers. In the timed RF amplifiers the center frequency may range from 1 to many megahertz and side frequencies extend to 5 or 10 kHz for amplitude modulated voice or music and to several hundred kilohertz for other amplifications.

• The Fig. 8.10.1 shows the tuned parallel LC circuit which resonates at a particular frequency. The resonance frequency and impedance of tuned circuit is given as,

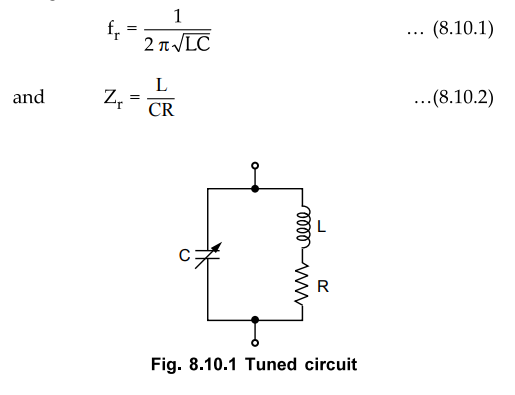
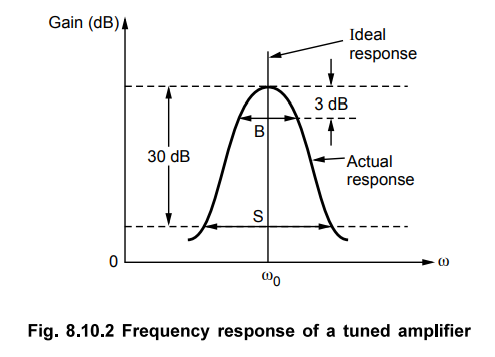
• The response of tuned amplifiers is maximum at resonant frequency and it falls sharply for frequencies below and above the resonant frequency, as shown in the Fig. 8.10.2. It is designed to reject all frequencies below a lower cutoff frequency, fL and above a upper cut-off frequency f_H’

• As shown in the Fig. 8.10.2, 3 dB bandwidth is denoted as B and 30 dB bandwidth is denoted as S. The ratio of the 30 dB bandwidth (S) to the 3 dB bandwidth (B) is known as skirt selectivity.

• At resonance, inductive and capacitive effects of tuned circuit cancel each other. As a result, circuit is like resistive and cos $ = 1 i.e. voltage and current are in phase. For frequencies above resonance circuit is like capacitive and for frequencies below resonance it is like inductive. Since tuned circuit is purely resistive at resonance it can be used as a load for amplifier.

a. Coll Losses

• As shown in Fig. 8.10.1, the timed circuit consists of a coil. Practically, coil is not purely inductive. It consists of few losses and they are represented in the form of leakage resistance in series with the inductor. The total loss of the coil is comprised of copper loss, eddy current loss and hysteresis loss. The copper loss at low frequencies is equivalent to the d.c. resistance of the coil. Copper loss is inversely proportional to frequency. Therefore, as frequency increases, the copper loss decreases. Eddy current loss in iron and copper coil are due to currents flowing within the copper or core cased by induction. The result of eddy currents is a loss due to heating within the inductors copper or core. Eddy current losses are directly proportional to frequency. Hysteresis loss is proportional to the area enclosed by the hysteresis loop and to the rate at which this loop is transversed. It is a function of signal level and increases with frequency. Hysteresis loss is however independent of frequency.

• As mentioned earlier, the total losses in the coil or inductor is represented by inductance in series with leakage resistance of the coil. It is as shown in Fig. 8.10.3.

b. Q Factor

•  Quality factor (Q) is important characteristics of an inductor. The Q is the ratio of reactance to resistance and therefore it is unitless. It is the measure of how 'pure' or 'real' an inductor is (i.e. the inductor contains only reactance). The higher the Q of an inductor the fewer losses there are in the inductor. The Q factor also can be defined as the measure of efficiency with which inductor can store the energy.

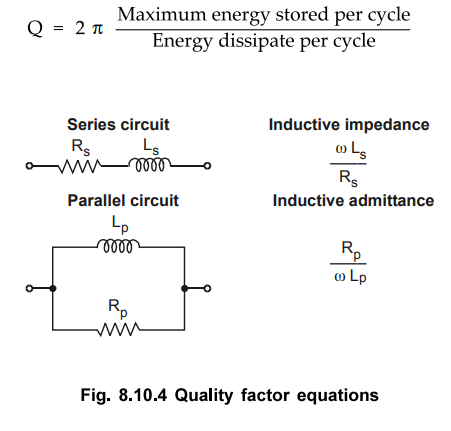
• The dissipation factor (D) that can be referred to as the total loss within a component is defined as 1/Q. The Fig. 8.10.4 shows the quality factor equations for series and parallel circuits and its relation with dissipation factor.

Quality factor equation Q = 1/D = ωLs / Rs = Rp / ωLp

Ex. 8.10.1 Derive the expression for quality factor, Q of an inductor.

Sol. : Consider a circuit shown in the Fig. 8.10.5. Here, a sinusoidal voltage Vmsin rot is applied to the inductor with an internal resistor R_s.

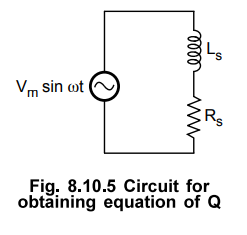
The maximum energy stored per cycle = 1/2 I2m Ls … (1)

and

Average power dissipated per cycle = ( I_m / √2)² R_s

Energy = power × Time

Average energy dissipated in the inductor per cycle

= Power × Priiodic time for one cycle = Power × T = ( I_m / √2)² R_s × T

= ( I_m / √2)² R_s × 1/f  T = 1/f

= I²_mR_s / 2f

Substituting equation (1) and (2) in the equation of Q. We have,

Ex. 8.10.2 Derive the expression for Q-factor of a capacitor.

Sol. :

1. Capacitor with a small resistor in series

• Consider a circuit shown in Fig. 8.10.6. Here, a sinusoidal voltage Vm sin oot is applied to the capacitor with a small resistor.

• Maximum energy stored in the capacitor per cycle = 1/ 2 C_s V²_max

where  V_max = Im / ωCs  when Rs >> 1 / ωCs

Maximum energy stored in the capacitor per cycle = 1/2 CV2max = I2m / 2 ω2Cs

Energy dissipated per cycle = I2m Rs / 2f

Substituting equation (1) and (2) in the equation of Q. We have,

2. Capacitor with a high resistor in parallel

• Consider a circuit shown in Fig. 8.10.7. Here, a sinusoidal voltage

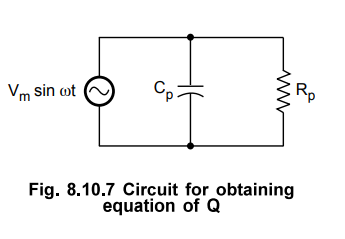
V_m sin ωt is applied to the capacitor with a high resistor in parallel.

Maximum energy stored in the capacitor = 1/2 CV²_max … (3)

Average power dissipated per cycle in Rp = (V_max/√2)² × 1/R_p = V²_max/2 R_p

Energy dissipated per cycle = V²_max/2 R_p × T = V²_max/2 R_pf   T = 1/f

Substituting equation (3) and (4) in the equation of Q we have,

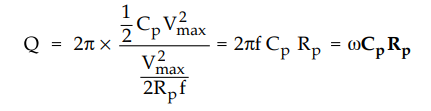
c. Unloaded and Loaded Q

• When the tank circuit is not connected to any external circuit or load, Q accounts for the internal losses and it is known as unloaded quality factor, Qv. It is defined as,

QU = 2π × Maximum energy stored per cycle / Energy dissipated per cycle in tank circuit

• In practice, the tank circuit is connected to the load. Hence, the energy dissipation takes place in the tank circuit as well as in the external load. The loaded quality factor, Q_L is defined as

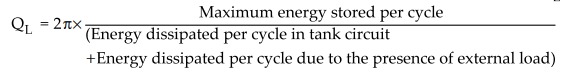
• Due to the loading, the equivalent parallel resistance Rp is reduced by any external resistance REXT placed in parallel with the circuit. Therefore, the loaded Q-factor is given by

QL = R_T / X_L = R_T / ωL_p

where, RT = R_p || R_EXT

• The quality factor QL determines the 3 dB bandwidth for the resonant circuit. The 3 dB bandwidth for resonant circuit is given as,

BW = f_r / QL

where f_r represents the centre frequency of a resonator and BW represents the bandwidth.

• If Q is large, bandwidth is small and circuit will be highly selective. For small Q values bandwidth is high and selectivity of the circuit is lost, as shown in the Fig. 8.10.8.

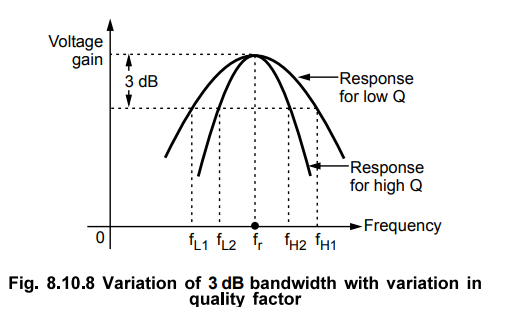
• Thus in tuned amplifier Q is kept as high as possible to get the better selectivity. Such tuned amplifiers are used in communication or broadcast receivers where it is necessary to amplify only selected band of frequencies.

Ex. 8.10.3 A tuned amplifier has its maximum gain at a frequency of 2 MHz and has a bandwidth of 50 kHz. Calculate the Q factor.

Sol. : Given : f_r = 2 MHz, BW = 50 kHz

We have Q = f_r / BW = 2 × 10⁶ / 50 × 10³ = 40

Ex. 8.10.4 A tuned amplifier is designed to receive AM broadcast of speech signal at 650 kHz. What is needed Q for amplifier?

AU : ECE : Dec.-09, Marks 2

Sol. : Given : fc = 650 kHz

Assume maximum modulating frequency for AM broadcast speech signal = 3 kHz.

Bandwidth = 2fm = 2 × 3 = 6 kHz

We have    Q = fr / BW = 650 kHz / 6 kHz = 108.33

d. Parallel Resonant Circuit

• The Fig. 8.10.9 shows the tuned parallel LC circuit which resonates at a particular frequency.

• The total admittance of the parallel tuned circuit is given by,

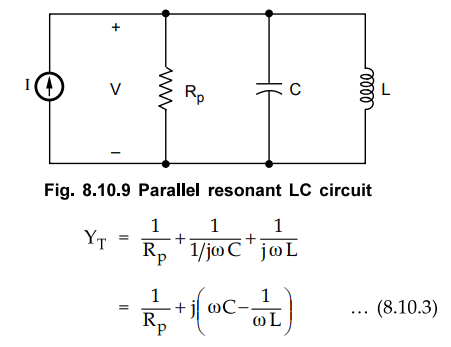
• At resonance imaginary part is zero, thus equating it to zero we get,

• In parallel resonant circuit, the voltage V is common to the three circuit elements, and we can write the maximum energy of the circuit in terms of the capacitance as C V2m/2. The energy loss per cycle is (V2m/2Rp). p- Then Q is

• Once the resonant condition is determined by O>-' L C = 1, the value of Q of a resonant circuit is determined by Rp , or by the ratio of C to L.

• At resonance, reactive term is equal to zero, therefore,

Y_T = 1 / R_p

Impedance at resonance, Z_o = R_p       ... (8.10.7)

• Using equation (8.10.6) and (8.10.7) we can write

Z₀ = Q ω₀ L = Q / ω₀ C   ...(8.10.8)

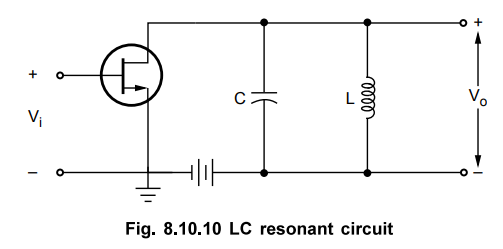
• The impedance of the resonant circuit is required in determining circuit gain. The gain of the circuit shown in Fig. 8.10.10 is

A_v = - g_m R_L = - g_m ω₀ L (8.10.9)

Ex. 8.10.5 A tank circuit contains an inductance of 1 mH. Find out the range of tuning capacitor value if the resonant frequency ranges from 540 kHz to 1650 kHz.

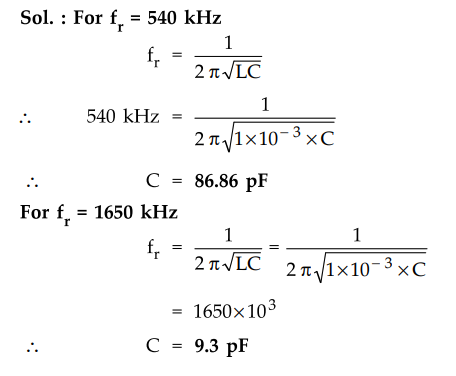
Ex. 8.10.6 A parallel resonant circuit has an inductance if 150 pH and a capacitance of 100 pF. Find the resonant frequency.

AU : ECE : May-07, Marks 2

Sol. : Given : L = 150 µH and C = 100 pF          

f0 = 1 / 2π√LC = 1 / 2π√150 × 10^-6 × 100 × 10^-12

= 1299.494 kHz

• Ex. 8.10.7 A parallel resonant circuit has a capacitor of 250 pF in one branch and inductance of 1.2 mH and a resistance of 10 Ω in the parallel branch. Find (1) resonant frequency (2) impedance of the circuit at resonance (3) Q-factor of the circuit.

Sol. : 1) Resonant frequency

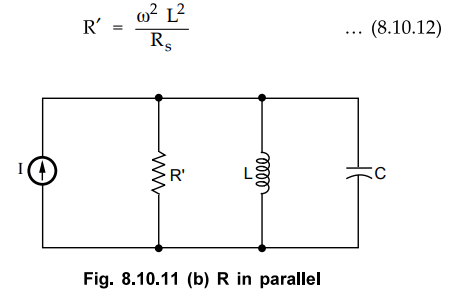
d. Series Resonant Circuit

• The Fig. 8.10.11 (a) shows the series resonant circuit. Here, the loss element Rs is n sries with L series branch is

• Usually at high Q conditions, ω² L² >> R²_a . Therefore, we can drop term R²_a in the denominator to get

Y = Rs / ω² L² + 1 / jωL

= 1 / R, + 1 / j ωL ... (8.10.11)

• This equation gives us the parallel arrangement as shown in Fig. 8.10.11 (b), where R' is given by

R = ω² L²  / R_s ... (8.10.12)

R_s =  ω² L²  / R_s  ... (8.10.13)

• The equations (8.10.12) and (8.10.13) represent transformations for passing from the series form of circuit to the parallel form, or vice versa. The inductance L does not change in the transformations but a small series Rs transforms to a large R' in parallel with L.

• In the previous section we have seen that for parallel circuit Q is

Q = ωo C Rp

• Here, Rp is represented by R'

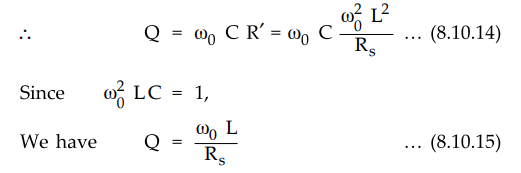
Ex. 8.10.8 An inductor of 250 pH has Q = 300 at 1 MHz. Determine Rg and R of inductor.

AU : ECE ; May-06, Dec.-12, Marks 2

Sol. :

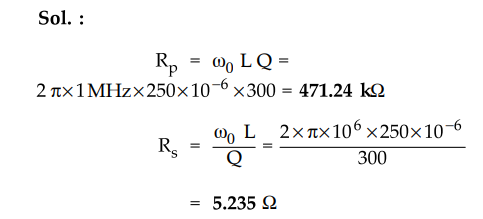
Ex. 8.10.9 A resonant circuit has C = 120 pF, L = 100 µH (with a series resistance of 5 ohms). Find the Q factor and the bandwidth of the circuit.

AU : ECE : Dec.-04, Marks 4

Sol. :

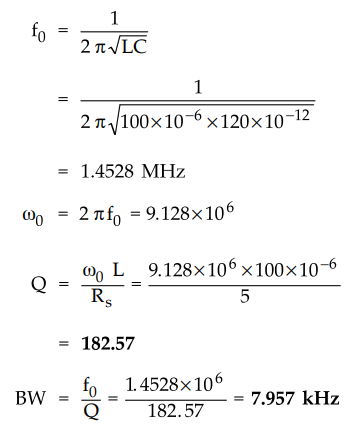
Ex. 8.10.10 A single tuned amplifier using n channel JFET with g_m = 5 mA/V and r_d = 20 k Ω, has tank circuit with L = 1 mH, series resistance of the coil R = 25 Q and C = 1 nF. Calculate the voltage gain at resonance if RL = 32 k Ω.

AU : ECE : May-05, Marks 2

Solution :

Ex. 8.10.11 The drain circuit of a FET tuned radio frequency amplifier has a 100 pF capacitor placed In parallel with an inductor L, whose unloaded Q-factor is 100. If the frequency of resonance is 1 MHz and the transistor output resistance is 20 kQ calculate the loaded Q-factor, inductance and loaded bandwidth.

AU : ECE : Dec.-11, Marks 8

Sol. : The total resistive loading on the tuned circuit consists of the transistor output impedance and the dynamic impedance in parallel R = RsRp/(Rs + Rp). The dynamic impedance using the unloaded Q-factor is

2. Signal Tuned Transistor Amplifier

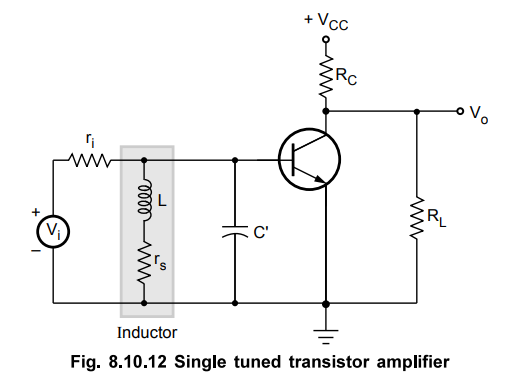
• A common emitter amplifier can be converted into a single tuned amplifier by including a parallel tuned circuit as shown in Fig. 8.10.12. The biasing components are not shown for simplicity.

• Before going to study the analysis of this amplifier we see the several practical assumptions to simplify the analysis.

Assumptions :

1. R_L << R_C  2. r_bb = 0

• With these assumptions, the simplified equivalent circuit for a single timed amplifier is as shown in Fig. 8.10.13.

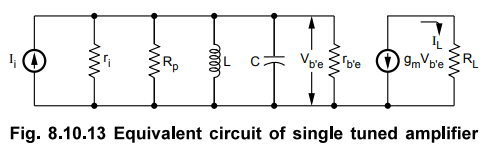
where          C = C' + Cb,e + (1 + g_m RL) C_bc

(1 + g_m RL) C_bc : External capacitance used to tune the circuit

(1 + g_m RL) C_bc The Miller capacitance

r_s : Represents the losses in coil

• The series RL circuit in Fig. 8.10.12 is replaced by the equivalent RL circuit in Fig. 8.10.13 assuming coil losses are low over the frequency band of interest, i.e., the coil Q high.

Qc ≡ ωL / r_s ... (8.10.16)

• The conditions for equivalence are most easily established by equating the admittances of the two circuits shown in Fig. 8.10.14.

We define the Q of the tuned circuit at the resonant frequenvy ω0 to be

• The Fig. 8.10.15 shows the gain versus frequency plot for single tuned amplifier. It shows the variation of the magnitude of the gain as a function of frequency.

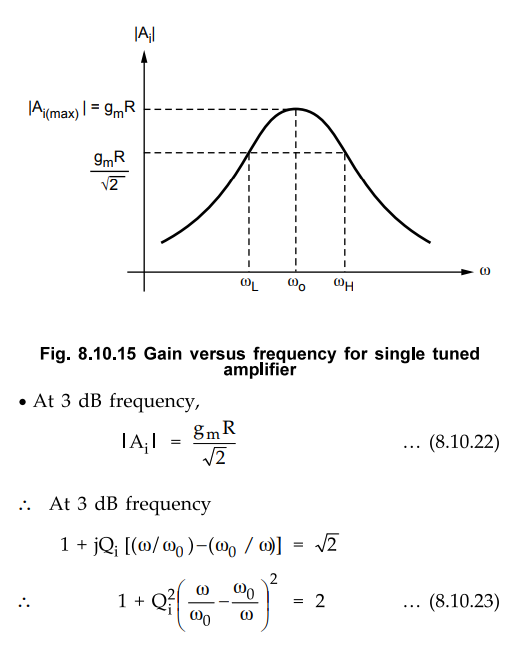
• This equation is quadratic in ω² and has two positive solutions, ω_H and ω_L .After solving equation (8.10.23) we get 3 dB bandwidth as given below.

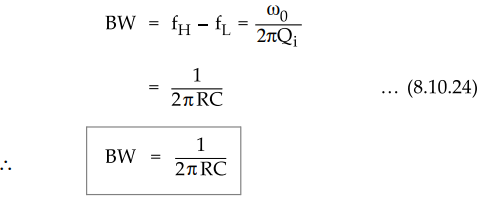
Ex. 8.10.12 Design a single tuned amplifier for following specifications : 1. Centre frequency = 500 kHz 2. Bandwidth = 10 kHz

Assume transistor parameters : gm = 0.04 S, hfe = 100, Cbe = 1000 pF and Cb,c = 100 pF. The bias network and the input resistance are adjusted so that ri = 4 kΩ and RL = 510Ω

Sol. : From equation (8.10.24) we have,

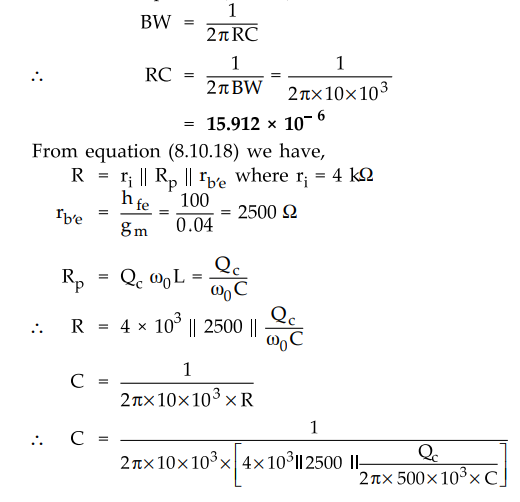
• The typical range for Qc is 10 to 150. However, we have to assume Q„ such that value of Cp should be positive. Let us assume Qc = 100.

3. Single Tuned FET Amplifier

• The Fig. 8.10.16 shows the single turned FET amplifier.

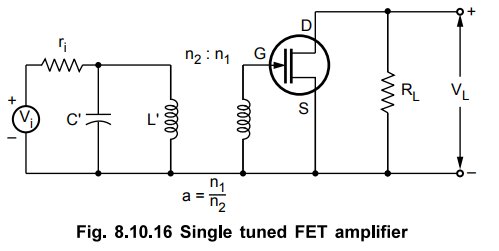
• The wquivalent circuit for the given amplifier is as shown in the Fig. 8.10.17.

• The voltage gain is given by,

Ex. 8.10.13 Design a tuned, amplifier using FET to have f0 = 1 MHz, 3 dB bandwidth is 10 kHz and maximum gain is - 10 FET has gm = 5 mA/V, rd = 10 K.

AU : May-06, Dec.-12, Marks 10

Sol. : The maximum gain of the amplifier is given by,