Singly Excited Magnetic System

Singly Excited Magnetic System

AU : May-03, 04, 05, 06, 09, 10, 11, 14, 16, 19, Dec.-02, 04, 09, 10, 13, 14, 16, 17, 18, April-03

• The analysis of singly excited magnetic system includes the derivations of expressions of electrical input energy, magnetically stored field energy and the mechanical force. Consider attracted type electromechanical armature relay as a singly excited magnetic system. It is shown in the Fig. 2.6.1. 

• The following assumptions are made while performing the analysis of singly excited magnetic system,

1. The resistance of the exciting coil is assumed to be present in lumped form, outside the coil. Thus coil is lossless and ideal.

2. The leakage flux does not take part in energy conversion process so it is neglected as practically it is small. Hence all the flux is confined to the iron core and links all the N turns of coil.

Thus if total flux is ϕ and turns of coil N then,

Flux linkages = Nϕ Wb-turns ... (2.6.1).

3. The leakage inductance is negligible.

4. There is no energy loss in the magnetic core. The reluctance of the iron path is neglected as negligible.

 

1. Electric Energy Input

• Due to the flux linkages λ, the reaction e.m.f. e exists, whose direction is so as to oppose the cause producing it i.e. voltage v according to Lenz's law as shown in the Fig. 2.6.1 This e.m.f. is given by,

e= dλ/dt .... (2.6.2)

• Applying Kirchhoff's voltage law to the coil circuit,

v = ir + e  ...(2.6.3)

ஃ       v = ir + dλ/dt  ...(2.6.4)

Multiplying both sides by i,

Vi = i² + dλ/dt  i

• Thus the magnetic system extracts the electric energy from the supply.

 

2. Magnetic Field Energy Stored

• Consider that the armature is held fixed at position X. As armature is not moving, the mechanical work done is zero. Hence according to energy balance equation, the entire electric energy input gets stored in the magnetic field.

ஃ dW_e = dW_f ... dW_m = 0

Key Point : This indicates that when moving part of any physical system is held fixed, then the entire electrical energy input gets stored in the magnetic field.

ஃ  dW_f= ei dt = i d λ = f dϕ ... (2.6.8)

• The relationship i - λ or f - ϕ is basically nonlinear for a magnetic circuit, similar to the B-H relationship. It shows hysteresis effect.

• From equation (2.6.8), the energy absorbed for a finite change in flux linkage can be obtained as,

• If the initial flux and flux linkages are zero i.e. Φ₁ = λ₁ = 0 then the energy stored in the magnetic field to establish the flux ϕ is given by,

• This is the energy stored in the magnetic field when the flux ois established in it.

Key Point : When a magnetic circuit undergoes a cycle ϕ₁ + ϕ₂ = ϕ₁, it undergoes a cycle of magnetization and demagnetization. The hysteresis and eddy current effects are dominant under such condition. Thus there is an irrecoverable energy loss due to hysteresis and eddy currents.

• In our analysis it is assumed that these losses are separated out and supplied by the electric source used. Hence the coil is ideal lossless coil. Such a magnetic system is called conservative system. 

• i - λ Relationship : The i - λ relationship is similar to the magnetization curve for a magnetic material for various values of x, the relationship is shown in the Fig. 2.6.2.

• Practically λ may vary according to i or i may vary according to λ. So mathematically this relationship is expressed as,

i = i (λ, x) ... λ = Independent variable

a = λ(i, x) ... i = Independent variable

 • Depending upon the independent variable the stored field energy is also the function of i, x or λ,

ஃ W_f =W_f  (λ,x) or W_f W_f (i, x)   ...(2.6.11)

Key Point : If x is changed then energy interchange takes place in magnetic coupling field and mechanical system. If x is held constant then energy interchange takes place between electric system and magnetic coupling field.

Concept of co-energy : When armature is held open then almost entire m.m.f. is required to drive the flux through air gap and hence magnetic saturation may not occur. So i - λ or f - ϕ relationship is linear in nature as shown in the Fig. 2.6.3.

This are OACO is complementary area of the i – λ rectangle and is defined as co-energy denoted as W_f

Key Point: The co-energy has no physical significance but it is important in obtaining magnetic forces.

• For a linear relationship between i and a without magnetic saturation,

Area OABO = Area OACO

The self induction L of the coil is defined as magnetic flux linkages per ampere.

The co-energy can be expressed for linear case as

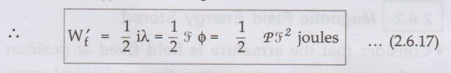
• From equation (2.6.16) it can be observed that field energy Weis function of two independent variables λ and x.

ஃ W_f(λ, x) = ½ λ² /L(x) ... (2.6.18)

where L(x) = Inductance as a function of x

• From equation (2.6.17) it can be observed that co-energy W’_f is function of two independent variables i and x.

ஃ W’_f (i, x)  = ½ L(x) i² ... (2.6.19)

• The equations (2.6.18) and (2.6.19) are general expressions for energy and co-energy.

 • Magnetic stored energy density : The magnetic energy density is the magnetic stored energy per unit volume. It is denoted as w_f

Key Point : The energy density expressions are important from the design point of view. The density value indicates capability of material to store energy. Thus proper dimensions so as to fully utilize the material, can be designed from energy density values.

Magnetic stored energy interms of B and H.

It is known that magnetic stored energy is given by,

This is magnetic stored energy.

i) The iron path having length Ii and Magnectic field intensity H1

ii) The air gap having length lg and magnectic field intensity Hg.

The total ampere turns supplied to establish the flux through iron path and air gap is Ni.

Ni = Ampere turns for iron path + Ampere turns for air gap

Ni = Hili + Hglg … (2.6.23)

λ = N ϕ = Total flux linkages … (2.6.24)

 

3. Mechanical Force

• Consider that the magnetic field produces a mechanical force F_f as shown in the   relay. This force drives the mechanical system consisting active and passive mechanical elements.

• Let the armature moves a distance dx in positive direction i.e. in the direction of force. The mechanical work done by the magnetic field then can be obtained as,

dW_m = F_f dx ...(2.6.29)

• As per the energy balance equation for electrical input,

• In such electromechanical systems the independent variables can be (i, x) or (λ, x).

Case 1 : The independent variables are (i, x) i.e. current constant

Thus λ changes as i and x hence

• As there is no term of di on left hand side of the equation, it should be zero on the right hand side as well.

• This is the expression for the mechanical force developed by the magnetic coupling field

• Rearranging the terms, the equation can be written as,

• Now iλ is total area of i - λ relationship while we is the energy stored in the field, as shown in the Fig. 2.6.4.

Key Point : This is the expression for system in which i is independent variable. This means input current constant. Such a system is current excited system.

Case 2 : The independent variables are (λ, x) i.e. a is constant.

Thus i changes as a and x hence,

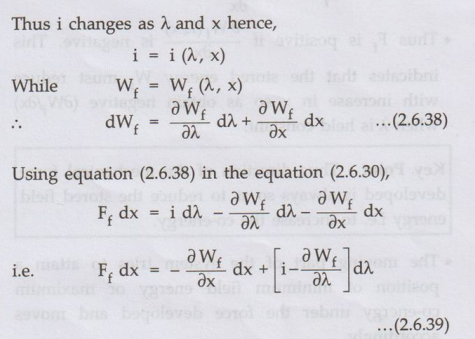
• There are no terms of dà on the left hand side of the equation, the corresponding term on the right hand side must be zero

Key Point : This is the expression for system in which à is independent variable i.e. flux producing voltage is constant. Such a system is voltage controlled system.

Thus use equation (2.6.37) for current excited system while equation (2.6.40) for voltage controlled system to find the mechanical force developed.

Rotational system : In rotational system, force is replaced by torque while linear displacement dx is replaced by angular displacement dθ.

• These are the expressions for the torque produced in rotational systems.

• Direction of mechanical force : Let us find out the direction of the mechanical force developed. It is known that,

F_f = - W_f(λ,x)/ ∂x

 • Thus F_f is positive if ∂W_f(λ,x)/ ∂x is negative. This indicates that the stored energy W_f must reduce with increase in x so as obtain negative (∂w_f/∂x) when ∂ is held constant.

Key Point : Thus direction of the mechanical force developed is always so as to reduce the stored field energy i.e. to increase the co-energy.

• The moving part of the system tries to attain a position of minimum field energy or maximum co-energy under the force developed and moves accordingly.

 

4. Determining Mechanical Force

 • Let us determine the mechanical force for non-linear and linear systems.

 Case 1: Non-linear

• In non-linear case, the derivatives must be obtained numerically or graphically by assuming small increment ∆x in x.

• Hence force can be expressed as,

Case 2 : Linear

 From equation (2.6.19) it is known that,

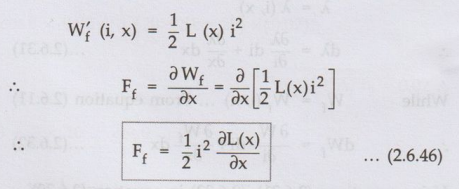
The direction of force is so as to increase x. This reduces the reluctance of the magnetic circuit.

The inductance depends on reluctance given by,

ஃ L= N²/S where S= Reluctance

So as reluctance decreases, inductance increases.

Key Point : Thus force F_f acts in the direction so as to increase inductance of the coil.

Similarly from equation (2.6.18) it is known that,

• These are the various expressions for the mechanical force developed in singly excited system.

• Thus following observation can be made about direction of mechanical force or torque developed in any physical system :

 The direction is so as,

1. Decrease the magnetic stored energy at constant λ.

2. Increase the stored energy and co-energy at constant i.

3. Decrease the reluctance.

4. Increase the inductance.

 

5. Mechanical Energy

• Consider that the armature of the system has changed its position from x₁ to x₂ as shown in the Fig. 2.6.5.

Case 1 : Coil current constant        

The current in the coil is constant say in i₀

 The flux linking changes from ϕ₁, to ϕ2, hence the flux linkages change from λ₁, and λ₂             

 Then the mechanical energy output is given by,

•  For non-linear case, the corresponding i – λ relationship is as shown in the Fig. 2.6.6 (a). 

•  For the linear case, i - λ relationship is shown in the Fig. 2.6.6 (b). From this it can be written that,

• This shows that half of the input electrical energy stored in the field while half is converted to mechanical output energy.

Key Point : Note that for this operation, the movement of armature from x₁ to x₂ must be very slow to keep coil current i₀ constant.

Case 2 : The flux linkages constant

The flux linkages with the coil are constant say  λ₀.     

The current changes from i₁, to i₂ .

It is known that for 2 to be independent variable, a is constant hence

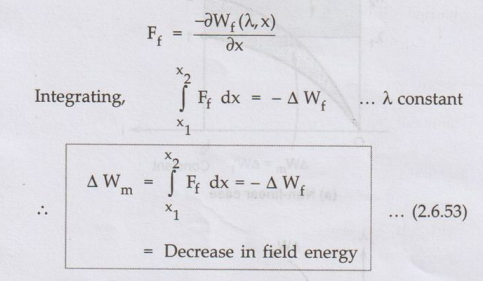
The negative sign indicates that there is decrease in the stored field energy.

For non-linear case, the corresponding i - λ relationship is shown in the Fig. 2.6.7 (a).

For the linear case, i – λ relationship is shown in the Fig. 2.6.7 (b) From this it can be written that,

• In both the linear and non-linear case, when a is constant, the change in input electrical energy is zero as the voltage is maintained constant.

ஃ  ∆W_e = 0    ... (2.6.55)

Key Point : For achieving this, the armature must move from position 1 to position 2 very quickly.

• As input energy is zero, the part of field energy stored is used to do the mechanical work. And thus stored energy decreases by same amount as equal to change in mechanical energy output.

• Practical case : Practically armature cannot move infinitely slow or it cannot move very fast instantaneously. So neither current can remain constant nor λ remains constant practically when armature moves from X₁ to X₂, the current decreases from i₁ to i₂, while flux linkages λ increases from λ₁ to λ2 .

 • The i-λ relationship for non-linear case is shown in the Fig. 2.6.8 (a) while for linear case it is shown in the Fig. 2.6.8 (b).

Key Point : Practically this area must be calculated numerically or graphically.

 

Ex. 2.6.1 The magnetic flux density on the surface of an iron face is 1.8 T which is a typical saturation level value for ferromagnetic material. Find the force density on the iron face. AU : April-03, May-11, Marks 8                                                   

Sol. : 

Negative sign shows that force direction is so as to reduce x as it is force of attraction

 

 

 Ex. 2.6.2 The  λ -i characteristics of singly excited electromagnet is given by I =121λ²x² for 0 <i < 4 A and 0 < x < 10 cm. If the air gap is 5 cm and a current of 3 A is flowing in the coil, calculate

 i) Field energy ii) Co-energy iii) Mechanical force on the moving part. AU : May-06, Marks 8

Sol. :

 

 

Ex. 2.6.3 In a rectangular electromagnetic relay, the exciting coil has 1500 turns of resistance 1 Ω. The cross-sectional area of the core A = 5 cm × 5 cm. Neglect the reluctance of magnetic circuit and fringing effects. If the coil is excited with an a.c. voltage of 50 Hz frequency, having peak to peak value of 100 V and the armature is held at a fixed distance of 1 cm, find the average force on the armature.

Sol. : The reluctance of magnetic circuit is to be neglected.

Ex. 2.6.4 The magnetic system shown in Fig. 2.6.9 has the following parameters : N = 500, i = 2A, Width of the air gap = 2.0 cm Depth of air gap = 2.0 cm, Length of air gap = 1 mm Neglect the reluctance of the core, the leakage flux and the fringing flux.

i) Determine the force of attraction between both sides of the air gap.

 ii) Determine the energy stored in the air gap.AU : Dec.-18, Marks 13

                       

Sol. : i) The stored energy density is given by,

 

Ex. 2.6.5 Sketch L(x) and calculate the induced emf in the excitation coil for a linear actuator shown in Fig. 2.6.10 (a) and (b). AU : Dec.-10, May-19, Marks 8

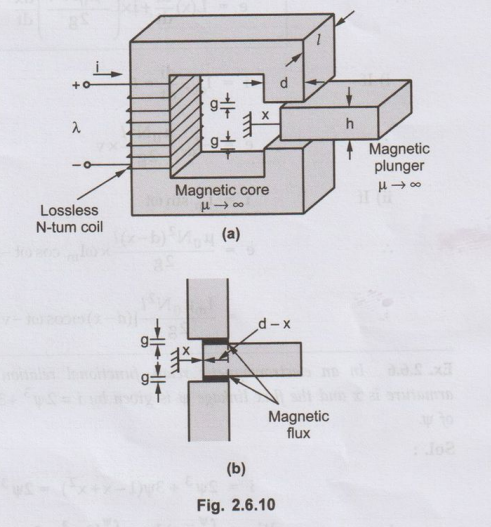
Sol. : The cross-sectional area of air gap is,        

 

Ex. 2.6.6 In an electromagnetic relay, functional relation between the current i in the excitation coil, the position of armature is x and the flux linkage ψ is given by i = 2ψ³ +3ψ(1- x+x²), x > 0.5. Find force on the armature as a function of ψ.U : Dec.-15, Marks 8

 Sol. :

 

Ex. 2.6.7 The electromagnetic relay shown in Fig. 2.6.11 is excited from a voltage source of v =  •√2 V sin wt. Assuming the reluctance of the magnetic circuit to be constant, find the expression for the average force on the armature, when the armature is held fixed at distance x. AU : Dec.-17, Marks 13

Sol. :

 

Review Questions

1. Derive an expression for co-energy density of an electromechanical energy conversion device. AU : Dec.-02,13, Marks 8

2. Explain about energy stored in magnetic system. AU : Dec.-16, May-03, Marks 8 

3. Derive expression for mechanical force developed by magnetic field. AU : May-04,10, Dec.-14,16,17, Marks 8     

4. Explain the i -  λ characteristic of a magnetic system. Also derive expression for co-energy density assume the i-λ relationship of the magnetic circuit is linear. AU : Dec.-04, Marks 16

5. Consider at attracted armature relay is excited by an electric. Explain about the mechanical force developed and the mechanical energy output with necessary equations. For linear and non-linear cases. AU : May-14, 16. Dec.-04, Marks 10

6. Explain the concept of singly excited machines and derive the expression for the electromagnetic torque.AU : May-05, 19, Marks 8

 7. Give the relation between field energy and the mechanical force developed in the field. AU : May-09, Marks 8

8. Discuss about field energy and coenergy in magnetic system.AU : May-11, Marks 4

 9. In a rectangular electromagnetic relay excited from a voltage source, the current and the flux linkages are related as i =  λ [λ +2(1-x)² ] where x < 1. Find the force on the armature as a function of  λ. 

(Ans. : 2λ²(1 – x))